B2.8 Démontrer la relation entre le numérateur d’une fraction et l’addition répétée de la fraction unitaire ayant le même dénominateur, à l’aide d’une variété d’outils et de schémas ainsi que de la notation fractionnaire usuelle.
Habileté : démontrer la relation entre le numérateur d’une fraction et l’addition répétée de la fraction unitaire ayant le même dénominateur
Le mot fraction vient du latin fractio qui veut dire « rupture ». Une partie d’un objet brisé peut donc représenter une fraction, car c’est une partie d’un tout. Toutefois, pour déterminer une fraction d’un objet divisé en plusieurs parties, il faut que les parties soient équivalentes. Précisons que lorsqu’il est question de parties équivalentes, il ne s’agit pas nécessairement de formes identiques, bien que celles-ci soient plus faciles à utiliser.
Il est important pour les élèves de comprendre que plus le tout est fractionné, plus ses parties sont petites.
Afin de concrétiser le fractionnement, il est recommandé de présenter des activités de manipulation, telles que le pliage et le découpage. Ces activités permettent un examen tactile de la quantité représentée par une fraction. En effet, le fractionnement de bandes de papier pour représenter des demis, des tiers, des quarts, des cinquièmes de bandes est un exercice formateur pour les élèves. Par la suite, ces bandes peuvent servir de modèles dans d’autres situations d’apprentissage. Ces activités d’apparence simple recèlent un potentiel étonnant! Les bandes fractionnaires sont utiles lorsqu’on veut compter en fractions unitaires.
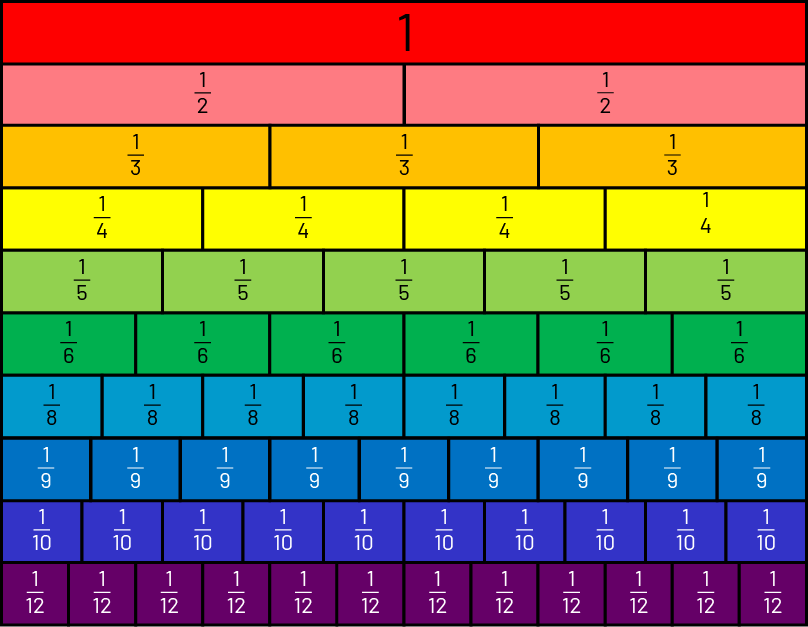
Les activités qui requièrent de compter les parties d’un tout, une à une, et de les mettre en relation avec le tout développent la compréhension du rôle du numérateur et du dénominateur. De plus, les élèves apprennent que le nom donné à chaque partie est déterminé par le nombre de parties retrouvées dans le tout. Ainsi, lorsqu’un tout est divisé en 2 parties équivalentes, il s’agit de demis; lorsqu’il est divisé en 3 parties équivalentes, il s’agit de tiers; lorsqu’il est divisé en 4 parties équivalentes, il s’agit de quarts. À partir de 5 parties équivalentes, on ajoute le suffixe ième au nombre de parties pour obtenir des cinquièmes, des vingtièmes, etc. L’élève qui maîtrise le concept de partie d’un tout n’a pas besoin de recréer l’image de la « tarte » pour comprendre, par exemple, que 6 sixièmes (\(\frac{6}{6} \)) forment un tout. Ainsi, afin d’identifier la fraction représentée ci-dessous, son raisonnement pourrait être le suivant : « Je compte les morceaux (1, 2, 3, 4, 5 et 6) et j’en conclus qu’il s’agit de sixièmes. Puisque cinq (5) parties sont ombrées, je peux affirmer que 5 sixièmes (\(\frac{5}{6} \)) de la figure sont ombrées. »
Afin de démontrer la relation entre le numérateur de la fraction \(\frac{5}{6} \) et l’addition répétée de la fraction unitaire ayant le même dénominateur, on demande aux élèves de compter les parties du tout ombrées en fractions unitaires. Par exemple, l’élève dirait « 1 un sixième », « 2 un sixième », « 3 un sixième », « 4 un sixième », « 5 un sixième ».
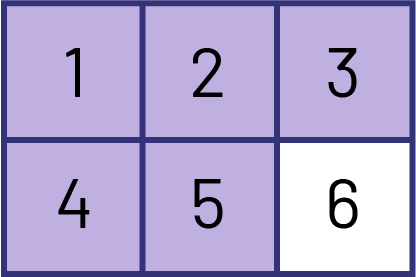
Ce processus les amène aussi à reconnaître qu’une fraction peut correspondre à la somme de fractions unitaires.
Exemple
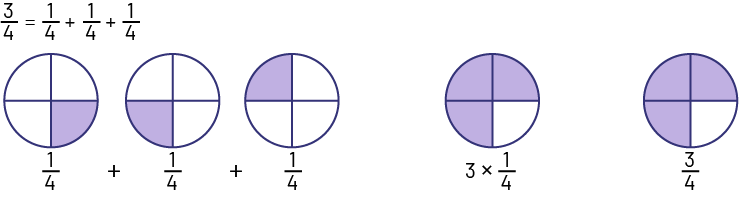Image L’addition de fractions suivante est représentée avec des cercles : 3 quarts égal un quart, plus un quart, plus un quart. 3 cercles sont divisés en 4 parties égales, une partie par cercle est ombragée. Cela représente un quart, plus un
quart, plus un quart. Un cercle est divisé en 4 parties égales, 3 de ces parties sont ombragées, cela représente : 3 multiplié par un
quart.
Un cercle est divisé en 4 parties égales, 3 de ces parties sont ombragées, cela représente : 3 quarts.
L’élève compterait les « un quart » : 1 un quart, 2 un quart, 3 un quart.
La soustraction se traite de la même façon. Par exemple, si je soustrais 3 huitièmes de 5 huitièmes, il reste 2 huitièmes. L’élève peut compter à rebours en fractions unitaires :
« 5 un huitième », « 4 un huitième », « 3 un huitième », « 2 un huitième ».
Les élèves qui ont compté, par exemple, des parties équivalentes de touts peuvent expliquer que le dénominateur représente ce qui est compté (par exemple, des quarts) et que le numérateur représente combien il y en a.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 33-35.
Connaissance : fraction unitaire
Fraction dont le numérateur est un (1) (par exemple, \(\frac{1}{3} \), \(\frac{1}{9} \)).
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 35.
Connaissance : numérateur
Nombre de parties équivalentes du tout dont se compose la fraction.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 34.
Connaissance : dénominateur
Nombre de parties équivalentes par lequel le tout est divisé.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 34.