B2.9 Utiliser les rapports de 1 à 2, de 1 à 5 et de 1 à 10 pour résoudre des problèmes, y compris des problèmes faisant appel au raisonnement proportionnel.
Habileté : utiliser les rapports pour résoudre des problèmes faisant appel au raisonnement proportionnel
L’habileté à utiliser un raisonnement proportionnel se développe tout au long de l’apprentissage des mathématiques.
L’analyse de relations de proportionnalité s’effectue en appliquant un raisonnement proportionnel. Ce raisonnement intervient lors de la comparaison de 2 rapports entre eux et de la reconnaissance d’une relation multiplicative.
En 3e année, l’étude des relations de proportionnalité porte plutôt sur la reconnaissance et sur la description de la relation multiplicative dans diverses situations de résolution de problèmes. Les élèves utilisent intuitivement le raisonnement proportionnel pour résoudre des problèmes impliquant 2 quantités qui sont dans un rapport de 1 à plusieurs (par exemple, 1 personne pour 10 doigts), de plusieurs à un (par exemple, 5 personnes par table) ou de plusieurs à plusieurs (par exemple, 4 litres de jus pour 8 personnes). Elles et ils utilisent aussi du matériel concret et divers modèles tels que des schémas, des fractions et des droites numériques.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 50-51.
Exemple 1
Dans cet ensemble de 9 billes ci-dessous, il y a un rapport de 1 à 2, \(\frac{1}{2} \) ou 1 : 2 entre le nombre de billes noires et le nombre de billes blanches.
Il y a 3 billes noires et 6 billes blanches. Cela signifie que les billes blanches représentent le double des billes noires. En utilisant une droite numérique double, le nombre du haut montre une graduation par un et le nombre du bas montre une graduation par 2. Dans cette mise à l’échelle de 1 : 2, on voit que les billes blanches représentent le double des billes noires.
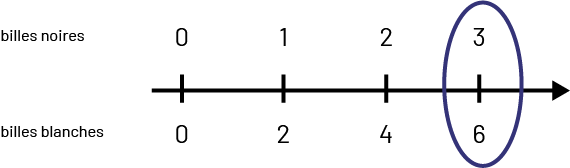Image Droite numérique qui représente les billes noires sur sa partie supérieure et les billes blanches dans sa
partie inférieure. Donc la droite est graduée de deux façons, au-dessus de la droite de zéro à 3 par intervalles réguliers de plus un.
La droite est graduée par en dessous de zéro à6x par intervalles réguliers de plus 2. La marque qui représente35 et 6
est encerclé.
Exemple 2
Le personnel enseignant demande aux élèves du cycle primaire de déterminer le nombre de morceaux que contiennent 3 tablettes de chocolat si une tablette contient 5 morceaux (rapport de 1 à 5). Il s’agit d’une relation multiplicative puisque le nombre de morceaux est 5 fois plus grand que le nombre de tablettes. Cependant, pour résoudre ce genre de problème, les élèves auront d’abord recours à l’addition répétée (\(5 + 5 + 5 \)). Par la suite, lorsqu’elles et ils auront été exposés au concept de multiplication, elles et ils pourront le résoudre en multipliant (\(3 \times 5 \)), ce qui constitue un premier pas vers l’utilisation d’un raisonnement proportionnel.
\(5 + 5 + 5\) ou \(3 \times 5\)
On peut représenter la relation de proportionnalité à l’aide d’une table de valeurs. Dans une table de valeurs qui représente une situation de proportionnalité, les rapports entre les quantités correspondantes sont équivalents.
| Tablettes | 1 | 2 | 3 |
|---|---|---|---|
| Rapport 1 : 5 | \(\times 5\) | \(\times 5\) | \(\times 5\) |
| Nombre de morceaux | 5 | 10 | 15 |
Alors, dans 3 tablettes de chocolat, il y a 15 morceaux.
Dans l’exemple ci-dessus, on reconnaît aisément la relation multiplicative par 5 entre le nombre de tablettes et le nombre de morceaux. De plus, cette table de valeurs permet d’établir des proportions (par exemple, \(\frac{1}{5} = \frac{3}{15} \))
Les élèves situent sur la droite numérique double des rapports équivalant à celui donné dans le but de résoudre le problème. Elles et ils peuvent choisir les rapports en fonction de leurs besoins et de leur compréhension du problème.
Exemple 3
Abdala achète du pain en vue de faire des sandwichs pour le pique-nique de l’école. Le coût du pain est de 2 $ pour préparer 20 petits sandwichs. Quel sera le coût du pain nécessaire à la préparation de 60 sandwichs?
En utilisant une droite numérique double, le nombre du haut montre une graduation par un, soit le coût du pain et le nombre du bas montre une graduation par 10, soit le nombre de sandwichs. L’élève sait que le rapport ici est 1 : 10 puisque la relation multiplicative entre 2 et 20 est de 10.
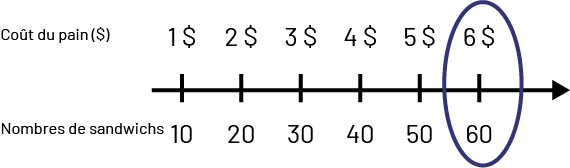Image Droite numérique qui représente le cout du pain en dollars, sur sa partie supérieure et le nombre de sandwichs,
dans sa partie inférieure. Donc la droite est graduée de deux façons, au-dessus de la droite de, un dollar à 6 dollars par intervalles réguliers
de plus un. La droite est graduée par en dessous de dix à 60 par intervalles réguliers de plus 20. La marque qui représente 6
dollars et 60 est encerclé.
Le coût du pain nécessaire à la préparation de 60 sandwichs est de 6 $.
Source : adapté du Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 52.
La relation multiplicative entre 2 rapports est à la base du raisonnement proportionnel. Les rapports sont présents dans le quotidien et dans plusieurs situations mathématiques, notamment dans les valeurs de position (par exemple, le rapport entre les unités et les dizaines est de 1 : 10), dans les fractions (par exemple, \(\frac{1}{5} \) ou 1 : 5), dans les figures semblables (par exemple, un agrandissement de 1 : 2), dans les unités de mesure du système métrique (par exemple, le rapport entre les mètres et les décimètres est de 1 : 10).
Les élèves doivent utiliser une variété de modèles dans le cadre d’activités pour développer leurs habiletés à raisonner proportionnellement. D’ailleurs, ces expériences informelles serviront à l’étude plus approfondie des rapports, des taux, des pourcentages et de l’algèbre dans les années d’études ultérieures.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 54.
Connaissance : raisonnement proportionnel
Le raisonnement proportionnel consiste à la base à voir les nombres selon leur valeur relative plutôt que leur valeur absolue.
Source : Qu’est-ce que le raisonnement proportionnel?, p. 3.
L’analyse de relations de proportionnalité s’effectue en appliquant un raisonnement proportionnel. Ce raisonnement intervient lors de la comparaison de 2 rapports entre eux et de la reconnaissance d’une relation multiplicative. À noter que les relations multiplicatives incluent l’opération de division, puisque toute division peut être transformée en multiplication (par exemple, diviser par 2 est l’équivalent de multiplier par \(\frac{1}{2} \)).
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 50.
Connaissance : relation de proportionnalité
Il y a une relation de proportionnalité entre 2 quantités lorsque ces quantités peuvent augmenter ou diminuer simultanément selon le même facteur.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 49.
Connaissance : rapport
Relation entre 2 grandeurs exprimées sous la forme du quotient des nombres qui les caractérisent.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 49.