B2. Sens des opérations :
Utiliser ses connaissances des nombres et des opérations pour résoudre des problèmes mathématiques de la vie quotidienne.
Situation d’apprentissage 1 : groupe de 2, de 3, de 4 ou de 5
Durée totale : environ 2 h 30 min
| Attente | Contenus d'apprentissage |
|---|---|
| B2. Sens des opérations utiliser ses connaissances des nombres et des opérations pour résoudre des problèmes mathématiques de la vie quotidienne. |
B2.6 Représenter la multiplication de nombres jusqu’à \(10 \times 10\) et la division de nombres jusqu’à \(100 \div 10\), à l’aide d’une variété d’outils et de schémas, y compris des dispositions rectangulaires. B2.7 Représenter et résoudre des problèmes relatifs à la multiplication et à la division, y compris des problèmes comprenant des groupes d’un demi, d’un tiers et d’un quart, à l’aide d’outils et de schémas. |
Intention pédagogique
Cette situation a pour but de permettre à l’élève :
- de représenter la multiplication à l’aide de matériel concret, d’une disposition rectangulaire ou d’une droite numérique;
- d’établir des liens entre les représentations concrètes, graphiques, verbales et symboliques de la multiplication.
Groupements égaux

4 groupes de 3
Disposition rectangulaire

4 rangées de 3
Droite numérique

4 bonds de 3
Préalables
Dans cette situation d’apprentissage, l’élève doit pouvoir :
- représenter des additions à l’aide de matériel concret et semi-concret;
- communiquer les additions à l’aide de phrases mathématiques;
- utiliser les faits d’addition jusqu’à 18 (\(9 + 9\)).
Vocabulaire mathématique
multiplication, groupements égaux, produit, facteur
Matériel
- annexe 3SO.1 (Jeu des cercles et des points) (1 copie par élève)
- annexe 3SO.2 (Qu’est-ce qu’on trouve chez nous en groupes de 2, de 3, de 4 ou de 5?) (1 copie par élève)
- grandes feuilles de papier
- jetons
- feuilles de papier
Avant l’apprentissage (mise en train)
Durée : environ 50 minutes
Utiliser les illustrations de la série de livrets de lecture, soit Le nombre deux, Le nombre trois, …, Le nombre dix, coll. « Chenelière mathématiques », pour stimuler la réflexion en ce qui a trait aux choses qu’on trouve en groupes de 2, de 3, de 4 ou de 5.
Grouper les élèves par 2 et leur demander de dresser leur propre liste des choses qu’on trouve en groupes de 2, de 3 de 4 ou de 5.
Rassembler les élèves et inscrire leurs idées dans un tableau sur de grandes feuilles de papier ou au tableau interactif.
| 2 | 3 | 4 | 5 |
|---|---|---|---|
|
Les roues d’une bicyclette Les yeux Les cornes d’un taureau Les chaussettes et les souliers Les jumeaux |
Les roues d’un tricycle Les pieds d’un trépied Les côtés d’un triangle Les feuilles d’un trèfle Les triplets |
Les pneus d’une voiture Les pieds d’une chaise Les côtés d’un carré Les pattes d’un animal |
Les jours d’école Les doigts Les orteils |
Poser les questions suivantes :
- Est-il plus facile de trouver des exemples de choses qui sont en groupes de 2, de 3, de 4 ou de 5?
- Pour quel nombre a-t-il été le plus difficile de trouver des exemples?
Demander ensuite aux élèves de nommer des choses qu’on trouve en groupes de 6 (par exemple, les pattes des insectes), de 7 (par exemple, les jours de la semaine) et de 8 (par exemple, les tentacules d’une pieuvre). Inscrire les exemples fournis dans de nouvelles colonnes du tableau.
Proposer un problème en utilisant un exemple inscrit dans le tableau ci-dessus. Par exemple : « Une araignée a 8 pattes. Combien y a-t-il de pattes, s’il y a 3 araignées? »
Remettre des jetons aux élèves et leur demander de résoudre le problème et de noter leur démarche.
Inviter quelques élèves à faire part de leur solution et à expliquer leur démarche.
Partir des idées des élèves sur la création de groupements égaux de 8 jetons pour expliquer que la multiplication correspond à une addition répétée.
Poser les questions suivantes :
- Combien de groupes avez-vous formés? Combien de jetons y avait-il dans chaque groupement?
- Comment les groupes de jetons illustrent-ils le problème?
- Comment pourriez-vous utiliser l’addition pour déterminer le nombre total de pattes? (\(8 + 8 + 8\))
- Comment peut-on représenter 3 groupes de 8 par une multiplication? (\(3 \times 8\))
- Quel est le produit de \(3 \times 8\)?
- Quels sont les différents moyens de déterminer le produit de 3 et 8?
Se servir de jetons, de dessins, de dispositions rectangulaires, de mots et de phrases mathématiques pour résoudre d’autres problèmes avec les élèves (par exemple, « Un tricycle a 3 roues. Combien y a-t-il de roues, s’il y a 4 tricycles? »).
 Image Dans un tableau de regroupements, on peut voir dans la première case : 12 jetons. Dans la deuxième case : 12
dessins de cœurs. Dans la troisième case : Les jetons en disposition rectangulaire, ils sont placés sur 4 colonnes de 3 jetons.
Image Dans un tableau de regroupements, on peut voir dans la première case : 12 jetons. Dans la deuxième case : 12
dessins de cœurs. Dans la troisième case : Les jetons en disposition rectangulaire, ils sont placés sur 4 colonnes de 3 jetons.

Image Un tableau de regroupement : Le regroupement est fait avec des mots, 4 groupes de 3 donnent 12. Le regroupement est fait avec une phrase mathématique, 4 multiplié par 3 égal 12.
Pendant l’apprentissage (exploration)
Durée : environ 50 minutes
Placer des jetons et des feuilles de papier à la disposition des élèves.
Grouper les élèves par 2 et leur demander de composer d’autres problèmes en s’inspirant des idées inscrites au tableau.
Demander aux élèves de représenter leurs problèmes de multiplication de diverses façons sur une grande feuille.
Exemple
 Image Dans la première case d’un tableau, on peut lire « dans un visage, il y a 2 yeux. Combien y a-t-il d’yeux s’il
y a 5 visages? » Dans la deuxième case : les 5 visages sont illustrés. Dans la troisième case, on peut lire, 5 groupes de 2 donnent dix. Dans la quatrième case, la phrase mathématique, 5 multiplié par 2 égal dix.
Image Dans la première case d’un tableau, on peut lire « dans un visage, il y a 2 yeux. Combien y a-t-il d’yeux s’il
y a 5 visages? » Dans la deuxième case : les 5 visages sont illustrés. Dans la troisième case, on peut lire, 5 groupes de 2 donnent dix. Dans la quatrième case, la phrase mathématique, 5 multiplié par 2 égal dix.
Après l’apprentissage (objectivation / transfert de connaissances)
Durée : environ 45 minutes
Demander ainsi à chaque équipe de présenter son travail et de l’expliquer au reste de la classe.
Poser les questions suivantes :
- Que remarquez-vous au sujet des différentes représentations?
- Comment pouvez-vous expliquer à quelqu’un ce que signifie \(5 \times 2\)?
- Quel dessin peut-on faire pour représenter \(3 \times 6\)?
- Pouvez-vous composer un problème ayant \(3 \times 6\) comme phrase mathématique?
Poser des problèmes semblables afin d’approfondir la compréhension des élèves :
- Si un menuisier a 15 pieds (communément appelés pattes) de tabouret, combien de tabourets à 3 pieds peut-il fabriquer?
- S’il y a 14 roues attachées au support à vélos, combien y a-t-il de vélos?
- S’il y a 16 mains sur un banc, combien y a-t-il de personnes?
- S’il y a 24 pattes dans un champ, combien y a-t-il de chevaux?
Inviter les élèves à expliquer leur démarche pour résoudre chacun des problèmes.
Demander aux élèves d’écrire dans leur journal de mathématiques ce qu’ils ont appris au sujet de la multiplication.
Exemples de critères d’évaluation
L’élève :
- fait des groupements égaux pour représenter le concept de multiplication;
- explique le sens de la multiplication à partir de n’importe quel mode de représentation (matériel de manipulation, dessins, dispositions rectangulaires, mots ou phrases mathématiques);
- explique les relations entre les différents modes de représentation.
Différenciation pédagogique
L’activité peut être modifiée pour répondre aux différents besoins des élèves.
| Pour faciliter la tâche | Pour enrichir la tâche |
|---|---|
| Utiliser, au début, des nombres qui se prêtent bien au dénombrement par intervalles de 2, de 3 et de 5. |
|
Suivi à la maison
Jeu des cercles et des points
À la maison, l’élève peut :
- jouer au jeu des cercles et des points;
- composer et résoudre des problèmes de multiplication à partir de ce que l’élève trouve à la maison en groupes de 2, de 3, de 4 ou de 5.
Distribuer une copie des annexes 3SO.1 et 3SO.2 à chaque élève pour que l’élève puisse jouer à ces jeux avec un membre de sa famille.
Activité supplémentaire
La calculatrice défectueuse
Matériel
- calculatrice (1 par élève)
Proposer aux élèves d’utiliser une calculatrice pour déterminer le produit de multiplications.
Expliquer que toutes les touches peuvent être utilisées, sauf celle de la multiplication, car elle « ne fonctionne pas ».
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 185-191.
Situation d’apprentissage 2 : quelle est la relation?
Durée totale : environ 2 h 30 min
| Attente | Contenus d'apprentissage |
|---|---|
| B2. Sens des opérations utiliser ses connaissances des nombres et des opérations pour résoudre des problèmes mathématiques de la vie quotidienne. |
B2.1 Utiliser les propriétés des opérations, et démontrer les relations entre la multiplication et la division pour résoudre des problèmes et vérifier la vraisemblance des calculs. B2.6 Représenter la multiplication de nombres jusqu’à \(10 \times 10\) et la division de nombres jusqu’à \(100 \div 10\), à l’aide d’une variété d’outils et de schémas, y compris des dispositions rectangulaires. |
Intention pédagogique
Cette situation a pour but de permettre à l’élève :
- d’explorer les liens et les régularités qui existent entre les nombres et les diverses opérations.
| Contexte pédagogique | Préalables |
|---|---|
|
Les dispositions rectangulaires sont des outils très utiles pour développer le sens des opérations de multiplication et de division et une compréhension de leurs propriétés. Il est possible de trouver divers exemples de dispositions rectangulaires (par exemple, calendrier, plateau de jeu de dames, carreaux du plancher) et de s’en servir en situation d’apprentissage. Les élèves construisent d’abord des dispositions rectangulaires à l’aide de matériel concret (par exemple, jetons, cubes, carreaux) pour représenter des énoncés de multiplication ou de division. Puis, ils en construisent aussi à l’aide de quadrillés. Exemples 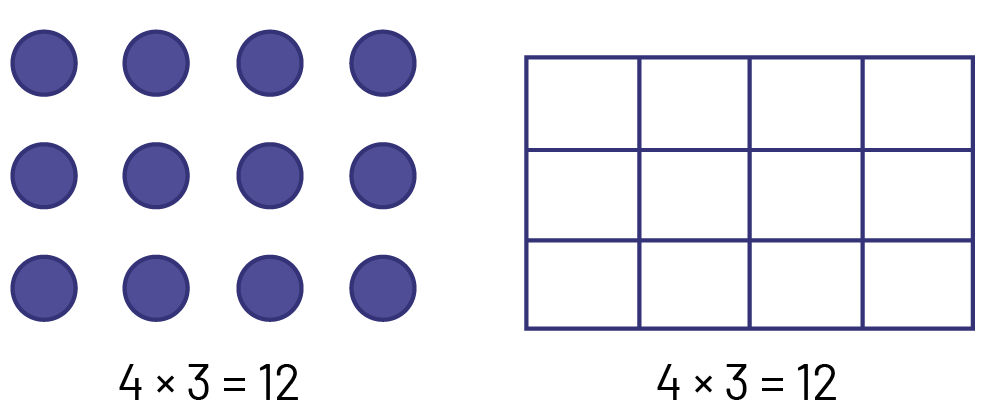
Au cycle moyen, les élèves sont en mesure d’utiliser un modèle plus abstrait de dispositions rectangulaires comme stratégie de multiplication et de division. Exemple 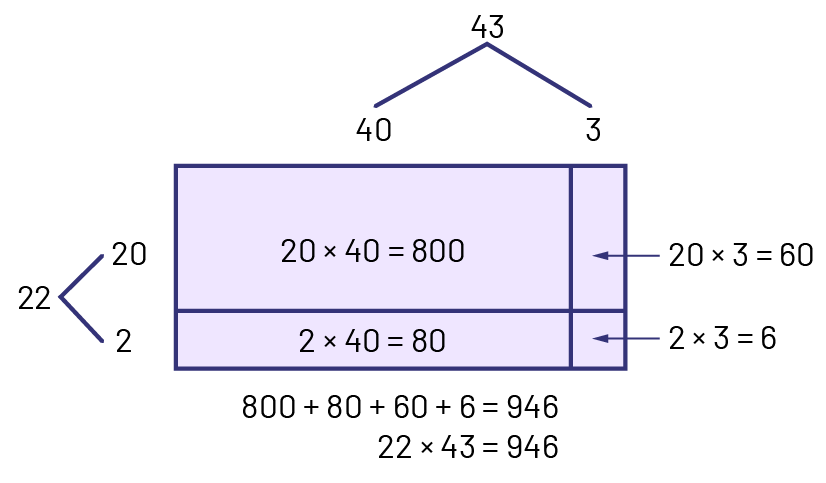 Image Modèle abstrait de disposition mathématique. LA disposition a 4 cases sur 2 rangées. Case un : 20 multiplié par 40 égal 800. Case 2 : 20 multiplié par 3 égal 60. Case 3 : 2 multiplié par 40 égal 80. Case 4 : 2 multiplié par 3 égal 6. À la gauche de la grille, on peut voir le 20 et le 2 qui sont additionnés, 20 plus 2 égal 22. Au-dessus de la grille, on peut voir le 40 et le 3 qui sont additionnés, 40 plus 3 égal 43. Sous la disposition rectangulaire on peut voir les phrases mathématiques : 800 plus 80 plus 60 plus 6 égal 946. 22 multiplié par 43 égal 946.
Image Modèle abstrait de disposition mathématique. LA disposition a 4 cases sur 2 rangées. Case un : 20 multiplié par 40 égal 800. Case 2 : 20 multiplié par 3 égal 60. Case 3 : 2 multiplié par 40 égal 80. Case 4 : 2 multiplié par 3 égal 6. À la gauche de la grille, on peut voir le 20 et le 2 qui sont additionnés, 20 plus 2 égal 22. Au-dessus de la grille, on peut voir le 40 et le 3 qui sont additionnés, 40 plus 3 égal 43. Sous la disposition rectangulaire on peut voir les phrases mathématiques : 800 plus 80 plus 60 plus 6 égal 946. 22 multiplié par 43 égal 946.
Les dispositions rectangulaires peuvent servir à représenter :
|
Dans cette situation d’apprentissage, l’élève doit pouvoir :
|
Vocabulaire mathématique
grille, disposition rectangulaire, rangée, colonne, parties égales, multiplier, diviser, additionner, soustraire, décomposer, répartir
Matériel
Activité principale
- annexe 3Rel.1 (1 jeu de cartes de nombre par équipe de 2)
- annexe 3Rel.2 (a) et annexe 3Rel.2 (b) (Mon cahier de dispositions rectangulaires) (1 copie par élève)
- grandes feuilles de papier
- cartons
- sacs en plastique réutilisables (1 par équipe de 2)
- jetons ou autres objets identiques (30 par équipe de 2)
- pailles ou crayons ou bouts de ficelle
- marqueurs de bingo, gommettes ou tampons encreurs
- papier quadrillé aux 2 cm
Avant l’apprentissage (mise en train)
Durée : environ 50 minutes
Préparer une grille de \(3 \times 4\) cases sur une grande feuille de papier et coller, sur les cases, des cartons de même couleur et de mêmes dimensions.
La déposer par terre et faire asseoir les élèves autour de sorte que tous puissent bien la voir.
Poser les questions suivantes :
- Que voyez-vous sur cette feuille? (par exemple, des cartons sur les cases d’une grille)
- Comment les cartons sont-ils disposés? (par exemple, en rangées et en colonnes)
- Pourquoi, selon vous, les cartons sont-ils disposés en rangées et en colonnes? (par exemple, c’est une organisation claire, en ordre, qui donne une bonne vue d’ensemble, qui évite la perte d’espace, qui permet de voir rapidement combien il y a d’objets)
- Combien de colonnes y a-t-il?
- Combien de cartons y a-t-il par colonne?
- Combien de rangées y a-t-il?
- Combien de cartons y a-t-il par rangée?
- Combien de cartons y a-t-il en tout?
- Quelles phrases mathématiques pourriez-vous utiliser pour décrire cette représentation?
- Connaissez-vous des endroits où les objets sont disposés en rangées et en colonnes comme s’ils étaient placés sur une grille? (par exemple, boîtes de céréales et de conserve dans une épicerie, chaises dans un gymnase, dalles d’une terrasse, autos dans un stationnement, œufs dans une boîte à œufs, arbres dans une plantation, plants de maïs dans un champ).
Note : Cette activité pourrait être modifiée pour le tableau interactif.
Pendant l’apprentissage (exploration)
Durée : environ 60 minutes
Lire le livre de Jill Bever et Sheila Currie, Les jardins de fourmis, et discuter des phrases mathématiques possibles à partir des dispositions rectangulaires dans les jardins.
Projeter 16 jetons disposés en 2 rangées de 8 jetons ou placer 16 objets sur le plancher en 2 rangées de 8 objets.

Demander aux élèves de décrire les différentes façons possibles de disposer les 16 jetons ou objets en colonnes ou en rangées égales (par exemple, les élèves peuvent observer qu’il y a 16 jetons ou objets disposés en 8 colonnes de 2 jetons ou objets ou en 2 rangées de 8 jetons ou objets);

Demander aux élèves de déterminer la phrase mathématique qui correspond aux divers groupements de jetons.
Exemples
\(4 + 4 + 4 + 4 = 16\)
\(4 \times 4 = 16\)
\(16 - 4 - 4 - 4 - 4 = 0\)
\(16 \div 4 = 4\)
Écrire les phrases mathématiques proposées par les élèves au tableau.
Former des équipes de 2 et remettre à chacune un sac contenant 30 jetons et un jeu de cartes préparé à l’aide de l’annexe 3Rel.1.
Demander aux élèves de :
- tirer une carte du sac;
- représenter, à l’aide de jetons, le nombre sous forme de disposition rectangulaire;
- placer des crayons, des pailles ou des bouts de ficelle sur la disposition rectangulaire de façon à représenter des groupements égaux de jetons;
- représenter d’autres groupements possibles.
Distribuer une copie des annexes 3Rel.2 (a) et 3Rel.2 (b) à chaque élève et leur demander :
- de reproduire les dispositions rectangulaires dans leur journal de mathématiques à l’aide de marqueurs à bingo, de gommettes ou de tampons encreurs;
- d’inscrire toutes les phrases mathématiques correspondant à chacune des dispositions rectangulaires.
Après l’apprentissage (objectivation / transfert de connaissances)
Durée : environ 40 minutes
Inviter chaque équipe à présenter une disposition rectangulaire différente et à expliquer ce qu’elle a fait.
Poser les questions suivantes afin de stimuler la discussion et la réflexion :
- Combien de dispositions rectangulaires différentes avons-nous créées?
- Qui a créé une disposition rectangulaire pour représenter le nombre 18? Qui a créé une disposition rectangulaire différente pour ce nombre?
- Quelles dispositions rectangulaires peut-on créer pour représenter le nombre 12?
- Explique la relation qui existe entre l’addition et la soustraction, entre l’addition et la multiplication.
- Explique la relation qui existe entre la multiplication et la division.
Exemples de critères d’évaluation
L’élève :
- crée diverses dispositions rectangulaires pour représenter un nombre;
- formule les phrases mathématiques correspondant aux diverses dispositions rectangulaires;
- explique la relation qui existe entre la multiplication et l’addition;
- explique la relation qui existe entre la multiplication et la division;
- utilise une phrase mathématique correspondant à une multiplication pour découvrir une phrase mathématique décrivant une division.
Différenciation pédagogique
L’activité peut être modifiée pour répondre aux différents besoins des élèves.
| Pour faciliter la tâche | Pour enrichir la tâche |
|---|---|
|
Demander à l’élève de découper différents rectangles représentant un nombre à l’aide de papier quadrillé aux 2 cm plutôt que des jetons, de les découper et de les coller dans son journal de mathématiques sous le nombre choisi. |
Suivi à la maison
Objets recyclés
À la maison, l’élève peut représenter un nombre en utilisant des objets recyclables tels que des attaches de sacs à pain, des onglets de canettes de boisson gazeuse, des petits cailloux, etc. disposés en rangées et en colonnes égales et décrire les dispositions rectangulaires que l’élève a faites.
Source : Guide de l’enseignement efficace des mathématiques de la 1re à la 3e année, p. 201-206.
