B2.7 Démontrer la relation entre l’addition répétée d’une fraction unitaire et la multiplication de cette fraction unitaire par un nombre naturel, à l’aide d’outils, de schémas et de la notation fractionnaire usuelle.
Activité 1 : multiplions une fraction unitaire par un nombre naturel
Afin d’effectuer une multiplication d’une fraction unitaire par un nombre naturel, les élèves doivent développer des stratégies personnelles en utilisant divers modèles. Prenons la situation suivante :
Lors d’une journée d’activités, on veut que les élèves vivent six activités différentes d’une durée d’un quart d’heure chacune. Quelle sera la durée de l’ensemble des activités?
Pour résoudre ce problème, on peut reconnaître qu’on peut effectuer l’opération \(6 \times \frac{1}{4}\). Afin d’en déterminer le résultat, diverses stratégies de calcul sont possibles telles que :
- effectuer l’addition répétée;
\(\frac{1}{4} + \frac{1}{4} + \frac{1}{4} + \frac{1}{4} + \frac{1}{4} + \frac{1}{4} = \frac{6}{4}\;\;\;{\rm{donc}}\;\;\;1\frac{2}{4}\;\;\;{\rm{ou}}\;\;\;1\frac{1}{2}\)
- utiliser une représentation concrète;
image Première horloge indiquant midi.La fraction un sur 4 est additionné à cette horloge et une
flèche montre le résultat vers la droite.Une deuxième horloge indique midi 15 minutes.Une série de 5 fractions d’un
quart est additionnée à cette horloge et des flèches pointent le résultat à droite.Une troisième horloge indiquant une
heure 30.
- utiliser une représentation semi-concrète;
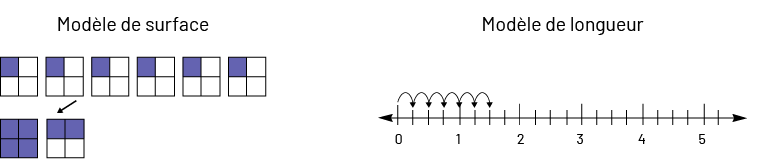image Image
un:Modèle de surfaceUne série de 6 carrés quadrillés comprenant chacun 4 carrés et dont le carré supérieur droit est
mauve.Une flèche part de cette série et pointe vers 2 autres carrés quadrillés de chacun 4 carrés.Le premier carré a
ses 4 carrés qui sont mauves. Le deuxième a 2 carrés sur 4 qui sont mauves.Image 2:Modèle de longueurDroite numérique
graduée de zéro à 5 par intervalles de zéro,25.6 flèches montrant des bonds de zéro,25 partent de zéro, ensuite
zéro,25, ensuite zéro,5, ensuite zéro,75, ensuite un et un,25.
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 95-96.
Activité 2 : comment représenter cet énoncé?
Demander aux élèves de représenter les énoncés suivants à l’aide d’une addition répétée et d’une illustration ou d’un schéma.
- \(\;2 \times \frac{1}{3}\;\)
- \(\;6 \times \frac{1}{5}\)
- \(\;4 \times \frac{1}{4}\;\)
- \(\;5 \times \frac{1}{{10}}\;\)
Activité 3 : multiplication
Selon le contexte, lorsqu’on multiplie :
- on peut répéter une quantité un certain nombre de fois dans le but d’obtenir une nouvelle quantité (par exemple, \(3 \times \frac{1}{2} = \frac{1}{2} + \frac{1}{2} + \frac{1}{2}\));
- on peut trouver un certain nombre de « groupe de » (par exemple, \(\frac{1}{2} \times 3 = \frac{1}{2}\;\;\;{\rm{groupe\;\;\; de\;\; }}\;3\))
Exemple
À chacun des 5 tournois auxquels il a participé, Maurice a gagné le tiers d’une caisse de balles de golf. Combien de caisses de balles a-t-il gagnées?
Source : Activité interactive : L’@telier – Ressources pédagogiques en ligne (atelier.on.ca).