B1.3 Arrondir les nombres naturels à la dizaine, à la centaine ou au millier près, dans divers contextes.
Habileté : arrondir des nombres naturels à la dizaine, à la centaine ou au millier près
Arrondir un nombre permet d’en faciliter l’utilisation. Cette méthode est souvent employée pour faire des estimations, mesurer et effectuer des comparaisons rapides.
Un nombre arrondi demeure près du nombre original selon la valeur de position à laquelle il est arrondi : plus la valeur de position est grande, plus l’approximation sera grande; plus la valeur de position est petite, plus l’approximation sera juste.
Le fait qu’un nombre soit arrondi vers le « haut » ou vers le « bas » dépend du contexte. Par exemple, dans une épicerie, les personnes peuvent arrondir à la hausse les prix pour s’assurer d’avoir suffisamment d’argent. Inversement, si elles regardent une pile de pièces de monnaie, elles pourraient vouloir arrondir à la baisse pour s’assurer encore une fois d’avoir suffisamment d’argent.
Hors contexte, on arrondit au nombre le plus près, par exemple :
- Si l’on arrondit 1 237 à la dizaine près, on obtient 1 240, puisque 1 237 est plus près de 1 240 que de 1 230.
- Si l’on arrondit 1 237 à la centaine près, on obtient 1 200, puisque 1 237 est plus près de 1 200 que de 1 300.
- Si l’on arrondit 1 237 au millier près, on obtient 1 000, puisque 1 237 est plus près de 1 000 que de 2 000.
Lorsqu’on arrondit un nombre à une valeur de position et que le chiffre à sa droite est 5 ou plus, la convention veut qu’on arrondisse le nombre vers le haut (sauf si le contexte suggère autre chose). Donc, si l’on arrondit 235 à la dizaine près, on obtient 240. À la suite de l’élimination de la pièce de 1 cent, les transactions en argent comptant sont maintenant arrondies aux 5 cents près.
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
Arrondissement
L’habileté à arrondir exige analyse et réflexion. L’opération ne se limite pas à l’arrondissement d’un nombre donné à une certaine valeur de position; elle nécessite aussi l’évaluation du contexte dans lequel le nombre se trouve. Les activités qui visent l’habileté à arrondir doivent alors être faites en contexte afin qu’elles permettent de refléter une utilisation authentique de l’arrondissement, de donner un sens à cet apprentissage, sens qui sera transféré au bagage cognitif des élèves.
Dans la vie courante, la décision d’arrondir provient de l’interprétation d’une situation et non d’une consigne reçue. Puis, la situation et le nombre en cause sont évalués pour désigner une valeur de position de l’arrondissement (par exemple, doit-on arrondir à l’unité de mille près ou à la centaine près?). La prochaine étape consiste à retenir des nombres repères en fonction de la position choisie (par exemple, pour arrondir 3 620 à la centaine près, certains élèves reconnaîtront mentalement ou sur une droite numérique la progression des centaines – 3 000, 3 100, 3 200, 3 300, 3 400, 3 500, 3 600, 3 700, alors que d’autres verront d’emblée que 3 620 se situe entre 3 600 et 3 700). Ainsi, en reconnaissant le nombre le plus près du nombre en cause (3 620), les élèves seront en mesure de déterminer la valeur arrondie du nombre. La dernière étape est celle de la communication du nombre arrondi. Bien sûr, certaines étapes se font de façon intuitive et presque automatiquement. Cette aisance vient précisément du sens du nombre; en d’autres termes, c’est l’utilisation de nos connaissances qui soutient ces décisions.
En salle de classe, plusieurs décisions ont souvent déjà été prises pour les élèves. C’est alors que les élèves interviennent, par exemple, pour arrondir un nombre comme 2 365 à la dizaine près, à la centaine près et à l’unité de mille près, ou encore simplement pour déterminer si 365 est plus près de 300 ou de 400. Il serait profitable pour leur apprentissage que les élèves aient l’occasion de prendre l’ensemble des décisions entourant l’arrondissement d’un nombre. Cela favorise le développement de leur sens critique de l’utilisation des nombres et approfondit leur sens de l’arrondissement.
Voici une situation qui illustre le raisonnement au cours de l’arrondissement de nombres. Les informations supplémentaires offrent quelques pistes pédagogiques.
Il y a généralement entre 3 000 et 4 000 spectateurs à la salle de spectacle « La Scène ». À la suite du spectacle, le préposé à la billetterie fait le décompte et détermine qu’il y a eu 3 736 spectateurs. Il croise la direction et décide de lui donner un aperçu des ventes de la soirée. Que dira-t-il à la direction?
| Raisonnement au cours des arrondissements | Raisonnement du préposé |
|---|---|
| Décider d’effectuer un arrondissement
Il est judicieux d’effectuer un arrondissement si le but est de communiquer une quantité en utilisant un nombre qui peut rapidement être significatif pour le destinataire. |
Dans l’exemple, si le préposé veut communiquer l’idée de grandeur des ventes et non la quantité exacte, il peut alors arrondir le nombre.
Cependant, s'il devait inscrire les nombres au grand livre de la comptabilité, il devrait alors utiliser le nombre exact. |
| Déterminer à quelle valeur de position se fera l’arrondissement
Il n’y a pas de règles quant au choix de la valeur de position. Cependant, le choix n’est pas arbitraire, car il dépend de l’interprétation de la situation et du sens du nombre de l’individu. Il est important de ne pas imposer systématiquement aux élèves d’arrondir à une certaine valeur de position, mais de discuter avec eux en donnant des exemples et des contre-exemples afin qu’elles et ils comprennent comment effectuer un choix judicieux. |
Si on vendait généralement entre 8 000 et 9 000 billets, l’arrondissement s’effectuerait à l’unité de mille près pour montrer qu’il y a une baisse importante des ventes. Dans l’exemple, le préposé décide d’arrondir à la centaine près étant donné que les ventes sont généralement entre 3 000 et 4 000 billets. S'il voulait que l’arrondissement donne un degré plus élevé de précision, il l’effectuerait à la dizaine près. |
|
Déterminer des nombres repères en fonction du choix de la valeur de position Le repérage de nombres aide les élèves à voir le nombre en relation avec d’autres nombres. L’utilisation de droites numériques permet de mieux saisir le sens du nombre et de visualiser la grandeur relative du nombre. Le repérage des nombres en fonction du regroupement donne de l’importance au regroupement choisi et permet de trouver les bornes d’un intervalle approprié pour compléter l’arrondissement. Il s’agit de reconnaître qu’un nombre tel que 3 736 est situé entre le nombre de centaines du nombre en question (37) et la centaine suivante (38).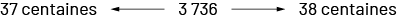 
Le repérage peut aussi se faire en reconnaissant un ensemble de valeurs reliées à la position choisie (par exemple, 3 000, 3 100, ...). Note : Il est très important que les élèves utilisent l’ensemble des positions lorsqu’elles et ils font des arrondissements. Par exemple, en cherchant à arrondir à la centaine près, des élèves ne retiendraient que le chiffre de la position en question et diraient, par exemple, que 3 736 se situe entre 7 centaines (700) et 8 centaines (800) et que donc l’arrondissement se fait à 700 (au lieu de 3 700). |
Dans l’exemple, le préposé détermine que 3 736 est situé entre 3 700 et 3 800.   |
| Arrondir le nombre
Les élèves doivent saisir que l’arrondissement s’effectue à une valeur proche du nombre. Par exemple, 3 736 s’arrondit à la centaine près à 3 700, car il est plus près de 3 700 que de 3 800. Note : Par convention, si le nombre est équidistant de deux valeurs, l’arrondissement s’effectue habituellement à la valeur la plus élevée des deux valeurs. Par exemple, 3 750 s’arrondit à la centaine près à 3 800. |
image Droite numérique graduée de 37 centaines à 38 centaines. 3700 est inscrit sous 37 centaines. 3800 est inscrit sous 38 centaines. Une flèche montrant le nombre 3736 pointant entre 3700 et 3800, plus près de 37 centaines. Une étoile représentant le nombre 3736 et une flèche partant de cette direction vers 37 centaines.   image Droite numérique graduée entre 2900 et 3800 par intervalles de 100. Une flèche désignant le nombre 3736 près du tiret 3700. Une étoile représente le nombre 3736 au-dessus de la droite. Une flèche partant de cette direction et allant vers le tiret 3700.
Dans l’exemple, le préposé doit comprendre que 3 736 est entre 3 700 et 3 800, mais qu’il est plus près de 3 700. C’est pourquoi l’arrondissement se fera à 3 700. |
| Communiquer l’arrondissement
Puisque l’arrondissement provient d’un contexte, la communication doit être faite en contexte. |
Le préposé pourrait mentionner à la direction qu’il y avait environ 3 700 spectateurs, un peu plus de 3 700 spectateurs ou même près de 3 700 spectateurs.
Note : Il serait faux d’affirmer qu’il y avait 3 700 spectateurs. |
En classe, les activités doivent permettre aux élèves de développer l’ensemble des habiletés à arrondir. Il est important que le personnel enseignant nuance ses propos au cours des activités d’arrondissement pour ne pas orienter la réflexion des élèves vers une stratégie ou une réponse en particulier. Jusqu’à présent, il a été question des arrondissements à une valeur de position près. Cependant, l’action « d’arrondir », au quotidien, peut se faire dans un sens plus large. Par exemple, une collecte de fonds a recueilli 14 345 $, et l’article du journal titrera : « Quel succès, l’événement a permis d’amasser près de 15 000 $! » Dans ce cas, on s’est servi de l’arrondissement pour « rendre rond » un montant d’argent, afin que l’information soit comprise rapidement. Voici quelques exemples de stratégies d’arrondissement possibles.
| Stratégies | Exemples |
|---|---|
| Définir un intervalle | S’il y a 3 736 personnes à un spectacle, on peut arrondir en disant qu’il y a entre 3 700 et 3 800 personnes. |
| Arrondir à un repère | Si chaque pomme coûte 44 ¢ et que nous en avons acheté une douzaine, on peut arrondir le prix à 50 ¢. |
| Arrondir en pensant à l’effet de l’arrondissement sur la quantité | Si on prépare des petits cadeaux pour chaque participant ou participante d’un concours, il est préférable d’en acheter un peu plus que le nombre de participants. Ainsi, s’il y a présentement 63 participants, on peut choisir d’arrondir à 70 et acheter 70 cadeaux afin de s’assurer d’en avoir suffisamment pour tous les participants. |
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 38-41.
Connaissance : approximation (estimation et arrondissement)
Les nombres ont été créés pour représenter des quantités avec un haut degré d’exactitude. En effet, ils apportent une précision que des termes comme « plus », « quelques », « des », « beaucoup » et « peu » ne donnent pas. Cependant, on peut aussi les employer pour montrer un certain ordre de grandeur de cette quantité. Dans ce cas, le nombre est utilisé pour représenter approximativement la quantité (par exemple, environ 200 personnes étaient à la fête ne signifie pas qu’il y en avait exactement 200). En général, l’approximation est une grandeur suffisamment près d’une grandeur connue (arrondissement) ou inconnue (estimation).
Les termes « arrondissement » et « estimation » sont souvent utilisés, à tort, de façon interchangeable. La différence fondamentale entre ces deux concepts réside dans la provenance du nombre. L’estimation provient de la relation entre une quantité inconnue et des connaissances antérieures, généralement sous forme de repères. L’arrondissement, lui, provient de la relation entre un nombre connu (précis ou approximatif) et sa proximité relative à d’autres nombres. Généralement, les estimations et les arrondissements servent à brosser un « portrait » plus clair de la quantité en question et à transmettre un sens de l’ordre de grandeur du nombre. Le tableau suivant, qui traite de l’exemple du prix d’une voiture, montre cette distinction.
| Arrondir un nombre | Estimer une quantité | |
|---|---|---|
| Définitions | Remplacer un nombre par une valeur appropriée à la situation, en suivant certains critères préétablis ou personnels. | Évaluer approximativement une quantité. |
| Exemples | Si le prix affiché d’une voiture neuve est 18 753 $, on peut dire qu’elle coûte environ 19 000 $. | En se promenant dans un stationnement, on remarque une voiture et on estime son prix à 20 000 $. |
| Explications | Le prix réel (nombre connu) a été arrondi au millier près. | Le prix ne repose sur aucune information précise reçue, mais sur des connaissances antérieures. |
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 35-36.