B1.5 Utiliser des schémas et des modèles pour représenter, comparer et ordonner des fractions représentant les portions individuelles provenant de deux scénarios de partage équitable d’une quantité entre n’importe quel regroupement de 2, 3, 4, 5, 6, 8 et 10 personnes.
Habileté : utiliser des schémas et des modèles pour représenter des fractions représentant les portions individuelles, provenant de deux scénarios de partage équitable
Différents modèles peuvent être utilisés pour représenter les fractions :
Les modèles d’ensemble comprennent des collections d’objets (par exemple, des billes dans un sac, des autocollants dans un livre d’autocollants), où chaque objet est considéré comme une partie égale de l’ensemble. Les attributs de l’ensemble (par exemple, la couleur, la taille, la forme) peuvent être pris en compte ou non. Soit chaque élément de l’ensemble peut être considéré comme un tout, soit l’ensemble complet peut être considéré comme un tout, selon le contexte du problème. Si l’ensemble complet est le tout, il est important que le modèle utilisé soit facilement fractionné. Par exemple, les mosaïques géométriques concrètes sont difficiles à fractionner alors que lorsqu’elles sont en papier, elles peuvent être facilement découpées.
Les modèles linéaires incluent des droites numériques, des réglettes et des segments de droite. Une position sur une droite numérique traite la fraction comme une relation partie-tout où le nombre 1 sur la droite numérique est 1 tout, le nombre 2 sur la droite numérique est 2 touts, etc. Par exemple, la fraction \(\frac{3}{4}\) a une position \(\frac{3}{4}\) située aux trois quarts du chemin entre 0 à 1.
D’autres modèles de mesure incluent la surface, le volume, la capacité et la masse. Le modèle de surface est le modèle le plus couramment utilisé avec des formes telles que des rectangles et des cercles. Les cercles sont difficiles à fractionner lorsque les fractions ne sont pas des demis, des quarts ou des huitièmes, il est donc important de fournir des modèles de cercles fractionnés. L’établissement de liens avec l’horloge analogique peut également être utile, par exemple, en représentant des durées comme \(\frac{1}{4}\) d’heure.
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
Habileté : utiliser des schémas et des modèles pour comparer et ordonner des fractions représentant les portions individuelles, provenant de deux scénarios de partage équitable d’une quantité
Un enseignement efficace et équilibré permet aux élèves de développer diverses stratégies pour comparer des nombres. De même, il doit permettre aux élèves de développer et d’approfondir leur compréhension de la valeur des fractions. C’est par le biais d’expériences concrètes et de représentations que les élèves apprennent à visualiser la valeur d’une fraction et à développer les stratégies pour les ordonner, les comparer et les mettre en relation avec d’autres nombres.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 44.
Pour estimer une quantité, les élèves doivent d’abord saisir le contexte et, pour cela, avoir recours à leur sens analytique et à leurs expériences personnelles. Ce bagage prend souvent la forme d’une représentation mentale et joue le rôle de repère visuel. On n’insistera jamais assez sur l’importance d’enrichir constamment ce bagage de référents visuels en faisant vivre aux élèves des situations variées dans divers contextes. Soulignons que les élèves qui sont exposés à des référents visuels et à du matériel de manipulation, tels que les cercles de fractions, les jetons, les bandes de carton et les réglettes, développent plus facilement leur sens de l’ordre de grandeur, qui est indispensable à l’estimation de la quantité représentée par une fraction.
Exemple
Regarder la tarte ci-dessous et demander aux élèves d’estimer la fraction de la tarte qui reste.

Voici un exemple de raisonnement d’élève :
- J’examine la tarte et je l’imagine séparée en deux. Je reconnais alors qu’il en reste plus qu’une moitié (\(\frac{1}{2}\)).

- Si elle est séparée en trois, je vois qu’il en reste moins que deux tiers (\(\frac{2}{3}\)).
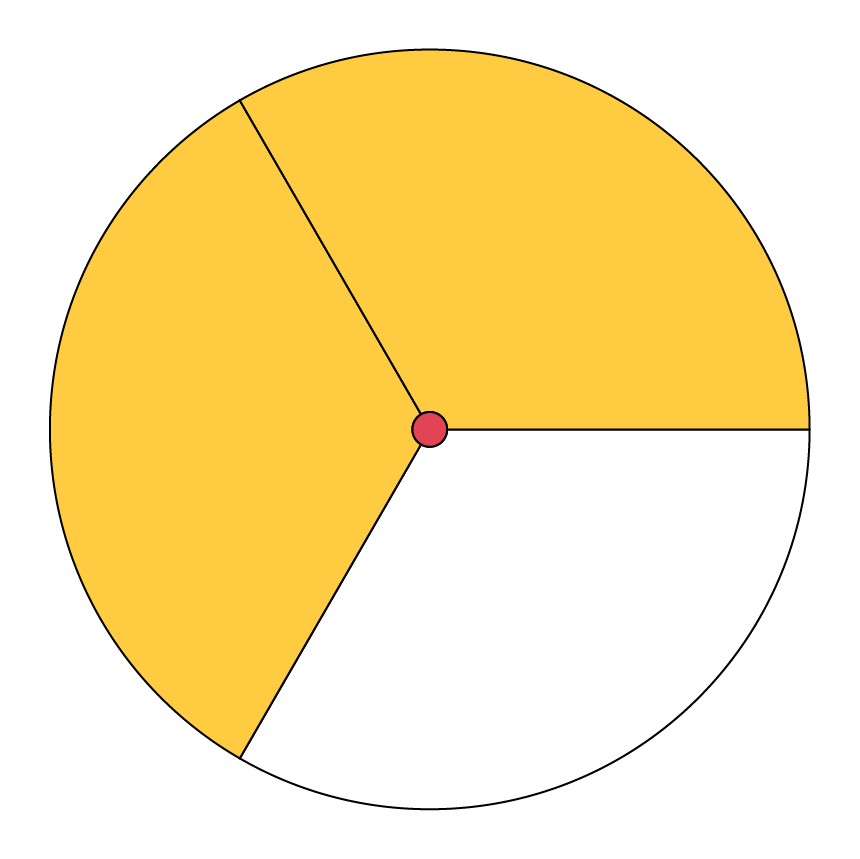
- Mais si elle est séparée en cinq morceaux égaux, je crois que c’est très près de l’équivalent de trois morceaux.
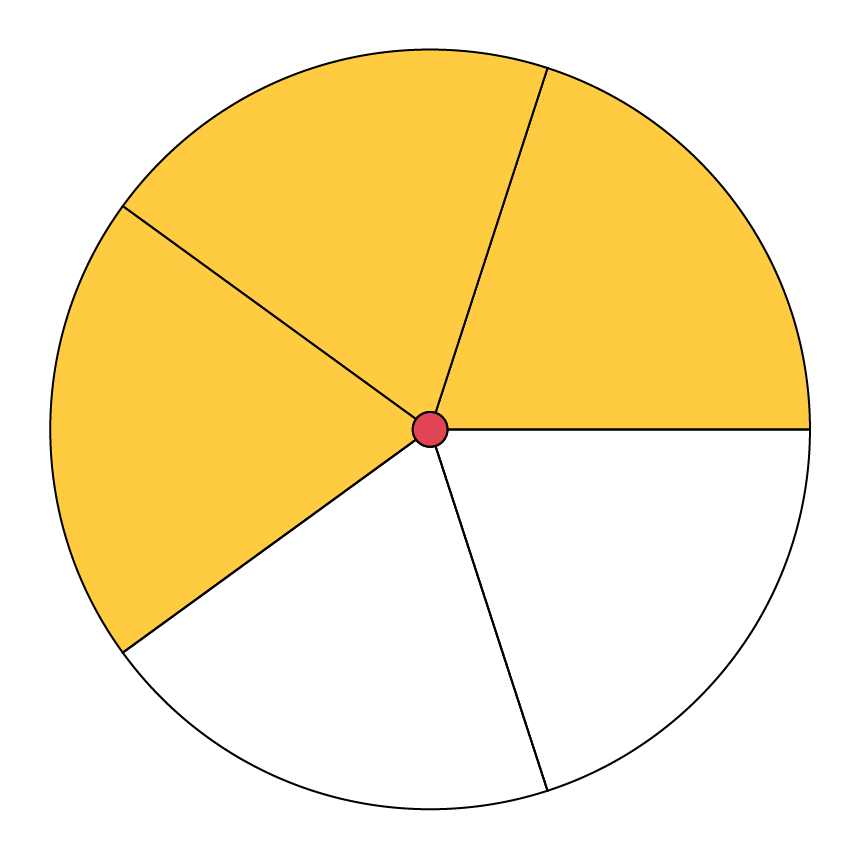
- Il reste environ \(\frac{3}{5}\) de la tarte.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 38-39.
Contexte pour la comparaison de fractions
Il est important que les élèves apprennent à toujours tenir compte du tout. Une fraction n’a aucun sens si elle n’est pas mise en relation avec un tout. Par exemple, on ne peut comparer une demi-pizza et un tiers de pizza si elles n’ont pas la même superficie à moins que l’on nous présente les pizzas en question. Le personnel enseignant doit présenter des situations d’apprentissage qui permettent aux élèves de découvrir qu’une fraction ne révèle rien de la taille du tout ou de ses parties; elle nous renseigne seulement sur la relation qui existe entre un tout et ses parties.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 31.
Relations d’ordre
Il est important que les élèves apprennent à ordonner des fractions en les comparant. L’habileté à ordonner et l’habileté à comparer doivent reposer sur les représentations des fractions que les élèves ont construites. Elles doivent découler de situations de résolution de problèmes qui permettent aux élèves de développer un sens de la valeur d’une fraction. C’est ce sens de la fraction qui permet aux élèves de comparer deux fractions et de conclure qu’une est plus grande que l’autre. Par opposition, l’enseignement qui se fait hors contexte tend à favoriser un apprentissage d’algorithmes qui néglige le sens de la fraction.
Les élèves du cycle moyen ont déjà des idées bien ancrées en ce qui a trait aux propriétés des nombres naturels. Or, lorsque les élèves commencent à travailler avec des fractions, les élèves font souvent face à un déséquilibre cognitif, c’est-à-dire une impression que ce qui était vrai ne l’est plus. Par exemple, les élèves ont appris qu’en présence de deux nombres naturels, le plus grand nombre indique une quantité plus grande. Les élèves tentent de transférer leurs connaissances et leurs compétences aux fractions. Ainsi, en voulant comparer \(\frac{1}{6}\) et \(\frac{1}{3}\), certains élèves croient que \(\frac{1}{6}\) est plus grand que \(\frac{1}{3}\), puisque 6 est plus grand que 3. Elles et ils se sentent en déséquilibre si elles et ils se font dire qu’elles et ils ont tort. Pour éviter de telles situations, l’apprentissage doit reposer sur un regard analytique de la fraction plutôt que sur un automatisme ou un algorithme.
Les activités qui amènent les élèves à comparer et à ordonner les fractions doivent favoriser la construction du sens de la fraction. Pour comparer des fractions, il est rarement nécessaire de chercher un dénominateur commun. Ainsi, il existe de nombreuses stratégies qui permettent de comparer des fractions. Généralement, la première stratégie apprise consiste en l’utilisation d’une représentation concrète ou semi-concrète des fractions en jeu. On peut recourir à cette stratégie, peu importe l’occasion. On peut aussi comparer les numérateurs si les dénominateurs sont identiques, ou comparer les dénominateurs si les numérateurs sont identiques. L’utilisation de fractions repères est une autre stratégie efficace.
Il est important de travailler à fond la comparaison des fractions avant l’équivalence des fractions. En effet, celle-ci est très complexe et la comparaison sert d’élément catalyseur à la compréhension des fractions équivalentes.
Comparaison de fractions en les représentant concrètement ou semi concrètement
Cette première stratégie consiste à représenter à l’aide d’un modèle les deux fractions en cause. Par exemple, comparons les fractions \(\frac{2}{5}\) et \(\frac{3}{8}\).
\(\frac{2}{5}\)

\(\frac{3}{8}\)

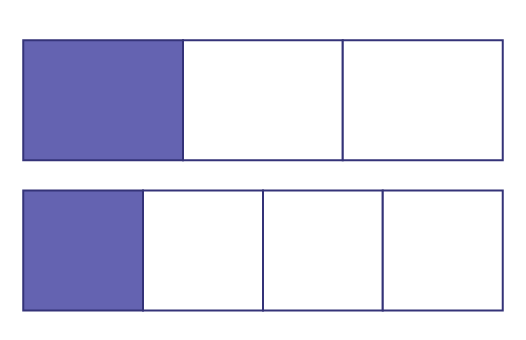
Donc, on peut conclure en comparant les deux représentations que \(\frac{2}{5}\; > \;\frac{3}{8}\). Il est très important de souligner, s’il s’agit de fractions d’un même tout, que le même modèle (tout) a été utilisé pour représenter les deux fractions. Les élèves négligent parfois l’importance du tout et n’interprètent pas correctement les situations avec des fractions. Par exemple, dans la situation suivante, en ne comparant pas le même tout, des élèves pourraient affirmer que \(\frac{1}{3} = \frac{1}{4}\).
\(\frac{1}{3}\)

\(\frac{1}{4}\)

Dans la situation représentée, il est vrai que \(\frac{1}{3}\)du premier rectangle correspond au \(\frac{1}{4}\)du deuxième rectangle. Mais afin de comparer les fractions d’un même tout, il aurait fallu les représenter à l’aide du même tout.
\(\frac{1}{3} > \frac{1}{4}\)
Comparaison de fractions ayant un dénominateur commun
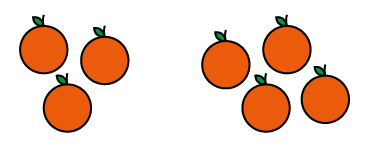
En 4e année, les élèves s’inspirent généralement de leurs connaissances antérieures et de leurs expériences avec les nombres naturels pour déterminer, sans difficulté, que \(\frac{4}{5}\) est supérieur à \(\frac{3}{5}\). Or, il arrive souvent que la réponse ne soit pas motivée par les bonnes raisons. En effet, beaucoup d’élèves ne font que comparer les numérateurs. Van de Walle et Folk (2005, p. 233) suggèrent au personnel enseignant de mettre l’accent sur le fait qu’il s’agit de parties de même taille ou de même nature. Ainsi en comparant \(\frac{4}{5}\)et \(\frac{3}{5}\), on souligne que \(\frac{4}{5}\) représente 4 parties d’une certaine taille et que \(\frac{3}{5}\) représentent 3 parties de cette même taille. On met ainsi l’accent sur la comparaison d’éléments de même nature (des cinquièmes), comme on le ferait si on comparait 3 oranges et 4 oranges.
3 cinquièmes et 4 cinquièmes d’un tout
 image 3 cinquièmes et 4 cinquièmes d’un tout.2 bandes sont représentées:Une bande divisée en 5 parties égales. Les 3 premières parties sont de couleur orange. Une bande divisée en 5 parties égales. Les 4 premières parties sont de couleur orange.
image 3 cinquièmes et 4 cinquièmes d’un tout.2 bandes sont représentées:Une bande divisée en 5 parties égales. Les 3 premières parties sont de couleur orange. Une bande divisée en 5 parties égales. Les 4 premières parties sont de couleur orange.
3 oranges et 4 oranges
Comparaison de fractions ayant un numérateur commun
En 4e année, les élèves sont en mesure d’accorder un sens aux nombres qui composent une fraction et d’entamer un processus réflexif afin de comparer deux fractions ayant un numérateur commun. Par exemple, comparons les fractions \(\frac{5}{9}\) et \(\frac{5}{6}\). Dans les deux cas, il y a 5 parties d’un tout. Lorsque le tout est divisé en 9 parties équivalentes, ces parties sont plus petites que celles du même tout divisé en 6 parties équivalentes. Ainsi, les neuvièmes sont plus petits que les sixièmes et on en a 5 dans les deux cas. Donc, \(\frac{5}{9}\) est plus petit que \(\frac{5}{6}\).
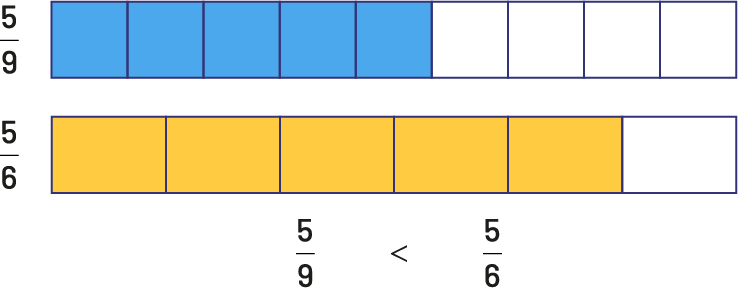 image La fraction 5 sur 9 est représentée par une bande divisée en 9 parties égales dont les 5 premières parties sont colorées en bleu.La fraction 5 sur 6 est représentée par une bande divisée en 6 parties égales dont les 5 premières sont colorées en jaune.Les 2 bandes ont la même longueur et on peut voir que le bleu représente une plus petite partie de la bande que le jaune de la deuxième bande.5 sur 9 est plus petit que 5 sur 6.
image La fraction 5 sur 9 est représentée par une bande divisée en 9 parties égales dont les 5 premières parties sont colorées en bleu.La fraction 5 sur 6 est représentée par une bande divisée en 6 parties égales dont les 5 premières sont colorées en jaune.Les 2 bandes ont la même longueur et on peut voir que le bleu représente une plus petite partie de la bande que le jaune de la deuxième bande.5 sur 9 est plus petit que 5 sur 6.
Pourtant, il n’est pas rare de voir des élèves penser le contraire, puisque 9 est plus grand que 6 et que les numérateurs sont les mêmes. D’où l’importance de s’attarder au sens du numérateur et du dénominateur et de développer l’habileté à visualiser des fractions.
Comparaison de fractions en utilisant des fractions repères
En 4e année, il est suggéré d’aider les élèves à développer leur sens de la fraction en ayant recours à des fractions repères. D’abord, les élèves se servent de trois repères, soit 0, \(\frac{1}{2}\) et 1. Elles et ils comparent ensuite des fractions données à ces repères. Voici quelques généralisations que les élèves sont en mesure de faire après avoir effectué un certain nombre d’activités d’apprentissage.
| \(\ 0\) | \(\frac{1}{2}\) | \(\ 1\) |
|---|---|---|
| Si le dénominateur d’une fraction est beaucoup plus grand que le numérateur, la fraction représente une petite quantité et la fraction est près de 0. Ainsi, \(\frac{3}{{25}}\) est près de 0. | Si le numérateur d’une fraction est à peu près la moitié du dénominateur, la fraction est près de \(\frac{1}{2}\). Ainsi, \(\frac{3}{8}\) est près de \(\frac{1}{2}\). On pourrait ajouter que \(\frac{3}{8}\) est légèrement inférieur à \(\frac{1}{2}\), car \(\frac{3}{8}\) est inférieur à \(\frac{4}{8}\), soit \(\frac{1}{2}\). | Si le numérateur d’une fraction est à peu près égal au dénominateur, la fraction est près de 1, car elle représente presque entièrement le tout. Ainsi, \(\frac{9}{10}\) est près de 1. |
Voici un modèle semi-concret qui illustre ces exemples.

Pour comparer 2 fractions, les élèves peuvent comparer chacune à un de ces repères. Par exemple, si on veut comparer \(\frac{5}{{20}}\) et \(\frac{7}{8}\), on peut déterminer que \(\frac{5}{{20}}\) représente une quantité entre 0 et \(\frac{1}{2}\), alors que \(\frac{7}{8}\) représente une quantité entre \(\frac{1}{2}\) et 1. On peut donc conclure que \(\frac{5}{{20}}\) est plus petit \(\frac{7}{8}\).
Comparaison de fractions en utilisant d’autres aspects du sens de la fraction
Dans un environnement d’apprentissage axé sur la résolution de problèmes, les élèves peuvent découvrir de nombreuses stratégies de comparaison basées sur le sens de la fraction qu’elles et ils ont construit.
Exemple 1
On veut comparer \(\frac{8}{9}\) et \(\frac{2}{3}\). On peut remarquer qu’il manque une partie à chaque fraction pour faire un tout. On reconnaît ainsi que pour la fraction \(\frac{8}{9}\), il manque \(\frac{1}{9}\) pour faire 1, alors que pour la fraction \(\frac{2}{3}\), il en manque \(\frac{1}{3}\). Puisque la partie manquante \(\frac{1}{3}\) est plus grande que la partie manquante \(\frac{1}{9}\), alors \(\frac{8}{9}\) est plus près de 1 que \(\frac{2}{3}\). Ainsi, \(\frac{8}{9}\) est plus grand que \(\frac{2}{3}\).
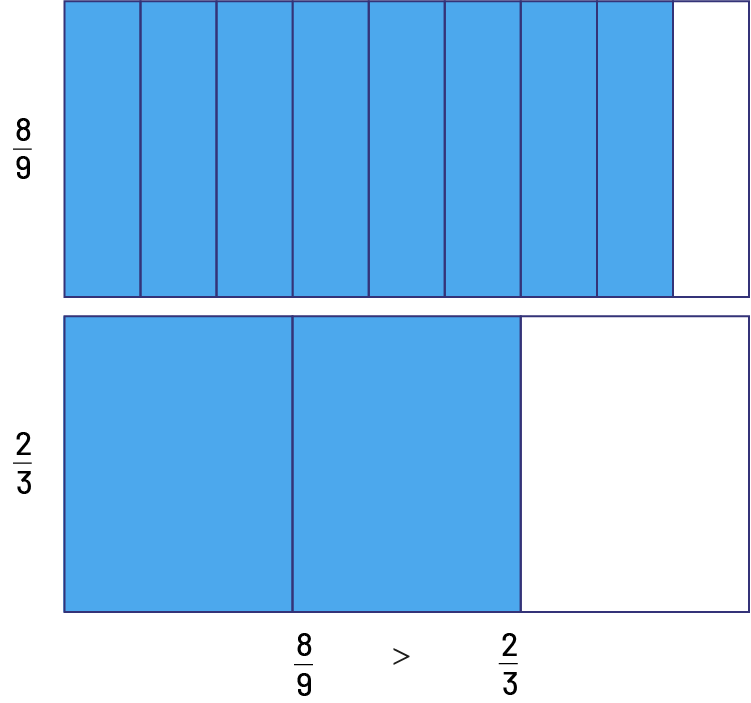 image La fraction 8 sur 9 est représentée par un rectangle divisé en 9 parties égales dont les 8 premières sont en bleu.La fraction 2 de 3 est représentée par un rectangle divisé en 3 parties égales dont les 2 premières sont en bleu.Les 2 rectangles sont de dimensions identiques. On peut y voir que les 8 parties en bleu du premier rectangle représentent une plus grande partie que les 2 parties en bleu du deuxième rectangle.8 sur 9 est plus grand que 2 sur 3.
image La fraction 8 sur 9 est représentée par un rectangle divisé en 9 parties égales dont les 8 premières sont en bleu.La fraction 2 de 3 est représentée par un rectangle divisé en 3 parties égales dont les 2 premières sont en bleu.Les 2 rectangles sont de dimensions identiques. On peut y voir que les 8 parties en bleu du premier rectangle représentent une plus grande partie que les 2 parties en bleu du deuxième rectangle.8 sur 9 est plus grand que 2 sur 3.
Exemple 2
On veut comparer \(\frac{2}{3}\) et \(\frac{7}{{12}}\). Les élèves pourraient utiliser leurs connaissances des fractions équivalentes pour conclure que \(\frac{2}{3}\) est plus grand que \(\frac{7}{{12}}\), car \(\frac{2}{3}\; = \;\frac{8}{{12}}\) et \(\frac{8}{{12}}\) représentent plus de parties de même taille que \(\frac{7}{{12}}\).
À la suite de l’apprentissage des divers concepts relatifs aux fractions, les élèves peuvent utiliser l’ensemble de leurs connaissances au sujet des fractions et l’ensemble des stratégies de comparaison de fractions pour résoudre des problèmes.
Exemple 3
Dans certaines courses automobiles (par exemple, formule 1), la ou le pilote qui franchit la 1re ou le 1er la ligne d’arrivée gagne et, à ce moment-là, la course se termine officiellement. Le classement des coureuses et coureurs n’est donc pas déterminé par l’ordre selon lequel elles et ils franchissent la ligne d’arrivée comme dans les courses traditionnelles, mais plutôt par la position des pilotes à la fin du parcours; cette dernière correspond à la fraction du circuit qu’elles et ils ont parcouru lorsque la 1re ou le 1er pilote franchit la ligne. Ce système permet d’assigner une position à tous les pilotes, même à ceux qui n’auraient pas terminé la course.
Voici la liste des fractions du circuit parcouru par chaque pilote à la fin de la course :
Wagner : \(\frac{8}{9}\); Villeneuve : \(\frac{2}{3}\); Trottier : 1; Munch : \(\frac{1}{4}\); Santana : \(\frac{7}{{10}}\); Burk : \(\frac{5}{6}\); Fround : \(\frac{3}{4}\); Colman : \(\frac{1}{9}\); Martina : \(\frac{5}{8}\).
Solution : Classement final de la course
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Trottier | Wagner | Burk | Fround | Santana | Villeneuve | Martina | Munch | Colman |
| \(\;1\) | \(\frac{8}{9}\) | \(\frac{5}{6}\) | \(\frac{3}{4}\) | \(\frac{7}{10}\) | \(\frac{2}{3}\) | \(\frac{5}{8}\) | \(\frac{1}{4}\) | \(\frac{1}{9}\) |
Source: Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 44-49.
Connaissance : partage équitable
Un partage équitable signifie que les quantités sont partagées en parts égales. Pour que les éléments d’un ensemble soient partagés également, l’ensemble doit être divisé pour que chaque personne reçoive la même quantité.
Un mot peut avoir plusieurs sens. Il est important de savoir que, dans de nombreuses situations, le mot « juste » ne veut pas dire « égal » et que le mot « égal » ne signifie pas nécessairement « équitable ». Le personnel enseignant doit clarifier la manière dont il utilise l’expression « partage équitable » et veiller à ce que les élèves comprennent que, dans le contexte des mathématiques, « équitable » signifie « égal » et que l’intention sous-jacente de ces problèmes de mathématiques est de déterminer des quantités égales.
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
