B1.9 Décrire les relations et représenter les équivalences entre des fractions et des nombres décimaux jusqu’aux dixièmes, dans divers contextes.
Habileté : décrire les relations et représenter les équivalences entre des fractions et des nombres décimaux jusqu’aux dixièmes, dans divers contextes
Il est important de reconnaître l’égalité entre les diverses représentations des nombres ou des expressions numériques. Dans le cadre des nombres décimaux, les élèves doivent reconnaître l’égalité entre un nombre décimal et une fraction correspondante.
Les élèves doivent comprendre que puisque la notation décimale n’est qu’une autre façon de représenter une fraction décimale, il est alors possible d’établir une relation d’égalité entre les deux notations (par exemple, \(\ 0,3 = \frac{3}{10} \)). En reconnaissant cette égalité, elles et ils sont en mesure d’associer une valeur de position à chacune des décimales qui composent un nombre décimal, par exemple, les dixièmes.
Exemple
Les élèves qui n’ont pas compris cette association sont parfois portés à représenter une fraction telle que \(\frac{2}{5}\)par 0,2 ou 0,25. La description ci-après décrit des comportements observables d’élèves ayant acquis une compréhension conceptuelle des nombres et du lien entre leurs différentes représentations.
Compréhension conceptuelle des nombres
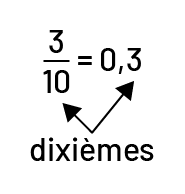
Nombre : 0,3
Comportements observables :
- L’élève peut en faire la lecture (trois dixièmes).
- L’élève peut écrire le nombre en notation fractionnaire, soit \(\frac{3}{{10}}\).
- L’élève peut représenter le nombre à l’aide de matériel concret ou semi-concret.
Exemple
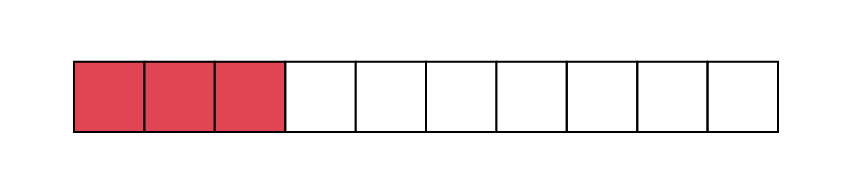
Nombre : \(\frac{6}{{10}}\)
Comportements observables :
- L’élève peut en faire la lecture (six dixièmes).
- L’élève peut écrire le nombre en notation décimale, soit 0,6.
- L’élève peut représenter le nombre à l’aide de matériel concret ou semi-concret.
Exemple

Nombre : \(\frac{2}{7}\)
Comportements observables :
- L’élève peut en faire la lecture (deux septièmes).
- L’élève sait que la fraction \(\frac{2}{7}\) n’est pas représentée par 0,2 puisqu’elle ou il sait que \(\ 0,2 = \frac{2}{10}\).
Pour établir la relation d’égalité entre une fraction dont le dénominateur n’est pas une puissance de dix (par exemple, \(\frac{1}{4}\)) et le nombre décimal correspondant, il est nécessaire de recourir au concept de fractions équivalentes. Par exemple, les élèves peuvent utiliser des bandes d’égales longueurs telles qu’illustrées ci-dessous pour constater que \(\frac{1}{4}\) se situe entre \(\frac{2}{{10}}\) et \(\frac{3}{{10}}\).
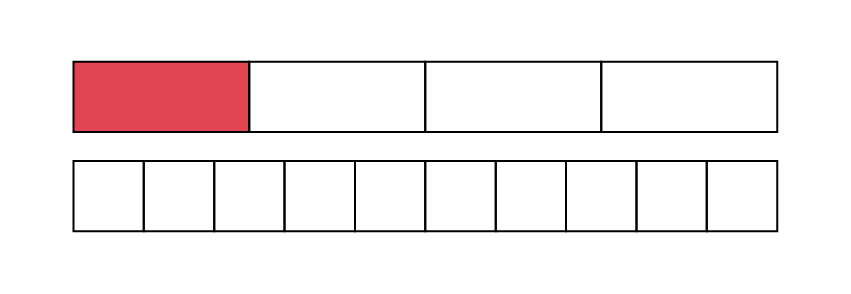
Ce genre d’exemple permet aux élèves de reconnaître que toutes les fractions qui peuvent être exprimées par une fraction décimale équivalente peuvent être représentées par un nombre décimal. C’est le cas notamment des fractions exprimées en demis et en cinquièmes comme le démontre le tableau suivant.
| Fraction | Fraction décimale équivalente | Nombre décimal |
|---|---|---|
| \(\frac{1}{2}\) | \(\frac{5}{{10}}\) | \[0,5\] |
| \(\frac{2}{5}\) | \(\frac{4}{{10}}\) | \[0,4\] |
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 46-48.
Connaissance : nombre décimal
Un nombre décimal est un nombre qui peut être exprimé en notation décimale avec une partie décimale finie.
Exemple
\(3,72\;{\rm{et}}\;{\rm{12}}{\rm{,135}}\;{\rm{64}}\)
L’ensemble des nombres décimaux inclut tous les entiers, car ces derniers peuvent être exprimés avec une partie décimale.
Exemple
\(3\; = \;3,0\)
Il inclut aussi certaines fractions, comme \(\frac{2}{5}\)et\(\frac{3}{{16}}\), puisque \(\frac{2}{5} = 0,4\) et \(\frac{3}{{16}} = 0,187\;5\). On remarque alors que\(\frac{1}{2}\),\(\frac{5}{{10}}\)et 0,5 sont des représentations symboliques du même nombre décimal.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 28.
Connaissance : fraction décimale
Tous les nombres décimaux peuvent être exprimés sous forme de fractions décimales, c’est-à-dire des fractions dont le dénominateur est une puissance de 10.
Exemple
\(3,7 = 3\frac{{7}}{{10}} = \frac{{37}}{{10}}\)
\(5 = 5,0 = \frac{5}{1}\)
Note : Les puissances de 10 sont 1, 10, 100, 1 000… On inclut 1 comme puissance de 10, car 100 = 1.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 28.
