B2.3 Utiliser des stratégies de calcul mental pour multiplier un nombre naturel par 10, 100 et 1 000 et pour diviser un nombre naturel par 10, et additionner et soustraire des nombres décimaux jusqu’aux dixièmes, et expliquer les stratégies utilisées.
Habileté : utiliser des stratégies de calcul mental pour multiplier un nombre naturel par 10, 100 et 1 000
L’habileté à utiliser le calcul mental pour multiplier par 10, 100 et 1 000 et diviser par 10 est basée sur le rapport de 10 : 1 qui existe entre les valeurs de position. Afin de bien représenter ce rapport, on utilise un tapis de valeur de position.
Lorsque l’élève multiplie par 10, elle ou il multiplie mentalement en visualisant le déplacement du facteur qui est multiplié par 10 d’une colonne vers la gauche dans un tapis de valeur de position.
Par exemple,
\( 3 \times 10\)
 image Tapis de valeur de position.De gauche à droite: centaines de mille, dizaines de mille, unités
de mille, centaines, dizaines, unités.3 fois dix.Dans la première ligne du tableau, il y a le chiffre 3 dans la
position des unités.Dans la deuxième ligne du tableau, il y a le chiffre 3 dans la position des dizaines et zéro
dans la position des unités. Une flèche part du zéro qui est dans la position des unités et va vers le 3 qui est
dans la position des dizaines.
image Tapis de valeur de position.De gauche à droite: centaines de mille, dizaines de mille, unités
de mille, centaines, dizaines, unités.3 fois dix.Dans la première ligne du tableau, il y a le chiffre 3 dans la
position des unités.Dans la deuxième ligne du tableau, il y a le chiffre 3 dans la position des dizaines et zéro
dans la position des unités. Une flèche part du zéro qui est dans la position des unités et va vers le 3 qui est
dans la position des dizaines.
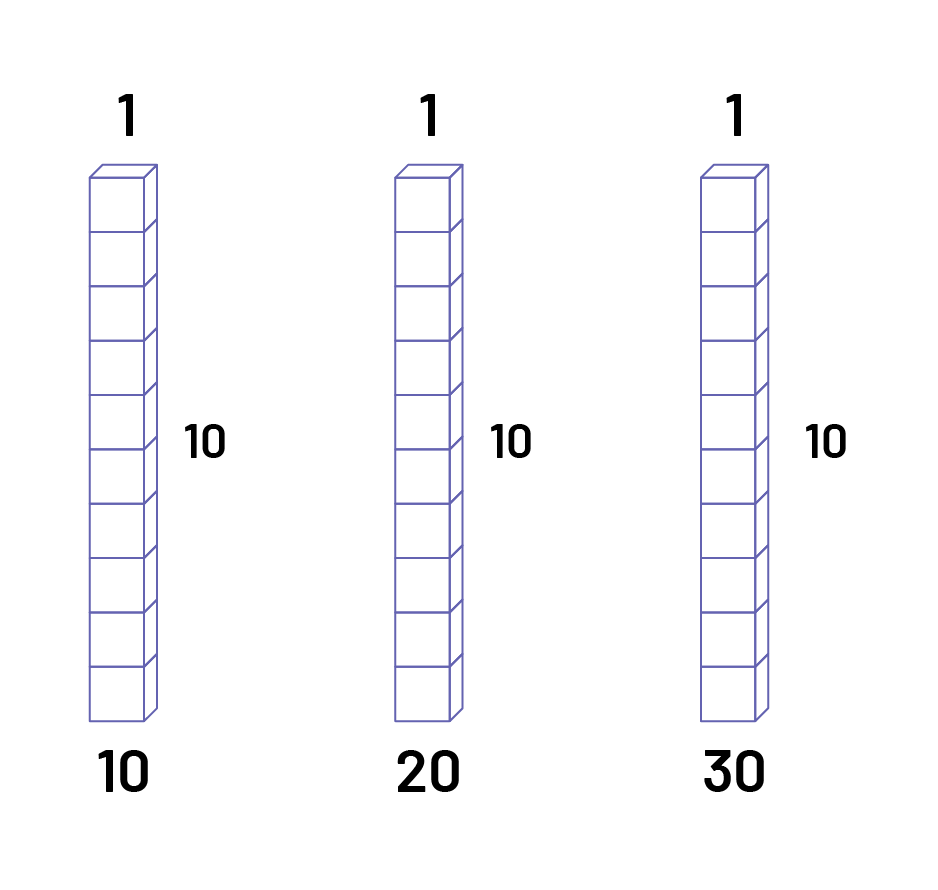
L’élève peut aussi visualiser 3 bâtonnets de\(\ 1 \times 10\) pour effectuer la multiplication\(\ 3 \times 10\).
 image
3 réglettes de dix unités chacune. Le chiffre un est inscrit au-dessus de chaque réglette. Le nombre dix est inscrit à
droite de chaque réglette. Le nombre dix est inscrit sous la première réglette, le nombre 20 est inscrit sous la
deuxième réglette et le nombre 30 est inscrit sous la troisième réglette.
image
3 réglettes de dix unités chacune. Le chiffre un est inscrit au-dessus de chaque réglette. Le nombre dix est inscrit à
droite de chaque réglette. Le nombre dix est inscrit sous la première réglette, le nombre 20 est inscrit sous la
deuxième réglette et le nombre 30 est inscrit sous la troisième réglette.
Alors, le produit de \(\ 3 \times 10\) est 30.
Lorsque l’élève multiplie par 100, elle ou il multiplie mentalement en visualisant le déplacement du facteur qui est multiplié par 100 de deux colonnes vers la gauche dans un tapis de valeur de position.
Par exemple,
\(\ 3 \times 100\)
 Tapis de valeur de position.De gauche à droite: centaines de mille, dizaines de mille, unités de
mille, centaines, dizaines, unités.3 fois 100.Dans la première ligne du tableau, il y a le chiffre 3 dans la
position des unités.Dans la deuxième ligne du tableau, il y a le chiffre 3 dans la position des centaines, zéro dans
la position des dizaines et zéro dans la position des unités. Une flèche part du zéro qui est dans la position des
unités et pointe vers le zéro qui est dans la position des dizaines. Une autre flèche part du zéro dans la position
des dizaines et pointe le chiffre 3 qui est dans la position des centaines.
Tapis de valeur de position.De gauche à droite: centaines de mille, dizaines de mille, unités de
mille, centaines, dizaines, unités.3 fois 100.Dans la première ligne du tableau, il y a le chiffre 3 dans la
position des unités.Dans la deuxième ligne du tableau, il y a le chiffre 3 dans la position des centaines, zéro dans
la position des dizaines et zéro dans la position des unités. Une flèche part du zéro qui est dans la position des
unités et pointe vers le zéro qui est dans la position des dizaines. Une autre flèche part du zéro dans la position
des dizaines et pointe le chiffre 3 qui est dans la position des centaines.
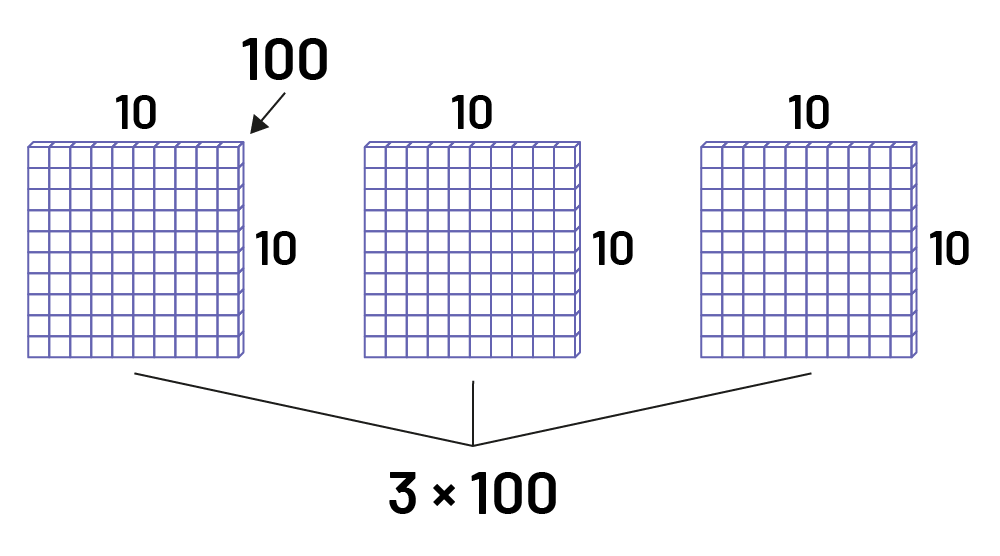
L’élève peut aussi visualiser 3 planchettes de\(\ 10\; \times 10\) pour effectuer la multiplication\(\ 3 \times 100\).
 image
Trois planchettes de dix par dix. Le nombre dix est écrit sur chaque dessus de planchette ainsi qu'à droite de chacune
des planchettes. Le nombre 100 avec une flèche montre qu’il y a 100 unités par planchette.Chacune des planchettes est
reliée par une ligne qui se joignent pour montrer l’équation 3 fois 100.
image
Trois planchettes de dix par dix. Le nombre dix est écrit sur chaque dessus de planchette ainsi qu'à droite de chacune
des planchettes. Le nombre 100 avec une flèche montre qu’il y a 100 unités par planchette.Chacune des planchettes est
reliée par une ligne qui se joignent pour montrer l’équation 3 fois 100.
Alors, le produit de \(\ 3 \times 100\) est 300.
Lorsque l’élève multiplie par 1 000, elle ou il multiplie mentalement en visualisant le déplacement du facteur qui est multiplié par 1 000 de trois colonnes vers la gauche dans un tapis de valeur de position.
Par exemple,
\(\ 3 \times 1\;000\)
 image Tapis de valeur de position.De gauche à droite: centaines de mille, dizaines de mille, unités
de mille, centaines, dizaines, unités.3 fois 1000.Dans la première ligne du tableau, il y a le chiffre 3 dans la
position des unités.Dans la deuxième ligne du tableau, il y a le chiffre 3 dans la position des unités de mille,
zéro dans la position des centaines, zéro dans la position des dizaines et zéro dans la position des unités. Une
flèche part du zéro qui est dans la position des unités et pointe vers le zéro qui est dans la position des
dizaines. Une autre flèche part du zéro dans la position des dizaines et pointe le chiffre zéro qui est dans la
position des centaines. Une autre flèche part du zéro dans la position des centaines et pointe le chiffre 3 qui est
dans la position des unités de mille.
image Tapis de valeur de position.De gauche à droite: centaines de mille, dizaines de mille, unités
de mille, centaines, dizaines, unités.3 fois 1000.Dans la première ligne du tableau, il y a le chiffre 3 dans la
position des unités.Dans la deuxième ligne du tableau, il y a le chiffre 3 dans la position des unités de mille,
zéro dans la position des centaines, zéro dans la position des dizaines et zéro dans la position des unités. Une
flèche part du zéro qui est dans la position des unités et pointe vers le zéro qui est dans la position des
dizaines. Une autre flèche part du zéro dans la position des dizaines et pointe le chiffre zéro qui est dans la
position des centaines. Une autre flèche part du zéro dans la position des centaines et pointe le chiffre 3 qui est
dans la position des unités de mille.
L’élève peut aussi visualiser 3 gros cubes de \(\ 10 \times 10 \times 10\) pour effectuer la multiplication\(\ 3 \times 1\;000\).
 image
3 gros cubes de 1000 unités. Chacun des 3 côtés des 3 cubes est indiqué par le nombre dix. Le nombre 1000 est écrit
au-dessus du premier cube. Le nombre 2000 est écrit au-dessus du deuxième cube. Le nombre 3000 est écrit au-dessus du
troisième cube.
image
3 gros cubes de 1000 unités. Chacun des 3 côtés des 3 cubes est indiqué par le nombre dix. Le nombre 1000 est écrit
au-dessus du premier cube. Le nombre 2000 est écrit au-dessus du deuxième cube. Le nombre 3000 est écrit au-dessus du
troisième cube.
Alors, le produit de\(\ 3 \times 1\;000\) est 3 000.
Habileté : utiliser des stratégies de calcul mental pour diviser un nombre naturel par 10
L’habileté à utiliser le calcul mental pour diviser par 10 est basée sur le rapport de 10 : 1 qui existe entre les valeurs de position. Afin de bien représenter ce rapport, on utilise un tapis de valeur de position.
Lorsque l’élève divise par 10, elle ou il divise mentalement en visualisant le déplacement de chaque chiffre du dividende d’une colonne vers la droite dans un tapis de valeur de position.
Par exemple,
\(\ 210 \div 10\)
 image Tapis de valeur de position.210 divisé par dix.De gauche à droite: centaines de mille,
dizaines de mille, unités de mille, centaines, dizaines, unités.Dans la première ligne du tableau, le chiffre 2 est
écrit dans la position des centaines, le chiffre un est écrit dans la position des dizaines et le chiffre zéro est
écrit dans la position des unités.Dans la deuxième ligne du tableau, le chiffre 2 est écrit dans la position des
dizaines et le chiffre un dans la position des unités.Une flèche part du chiffre 2 de la première ligne et pointe le
chiffre 2 de la deuxième ligne.Une autre flèche part du chiffre un de la première ligne et pointe le chiffre un de
la deuxième ligne.
image Tapis de valeur de position.210 divisé par dix.De gauche à droite: centaines de mille,
dizaines de mille, unités de mille, centaines, dizaines, unités.Dans la première ligne du tableau, le chiffre 2 est
écrit dans la position des centaines, le chiffre un est écrit dans la position des dizaines et le chiffre zéro est
écrit dans la position des unités.Dans la deuxième ligne du tableau, le chiffre 2 est écrit dans la position des
dizaines et le chiffre un dans la position des unités.Une flèche part du chiffre 2 de la première ligne et pointe le
chiffre 2 de la deuxième ligne.Une autre flèche part du chiffre un de la première ligne et pointe le chiffre un de
la deuxième ligne.
L’élève peut aussi visualiser 2 planchettes de\(\ 10 \times 10\) pour effectuer la division \(\ 210 \div 10\). Elle ou il peut décomposer 210 en 100 + 100 + 10 pour ensuite diviser chacun par 10.
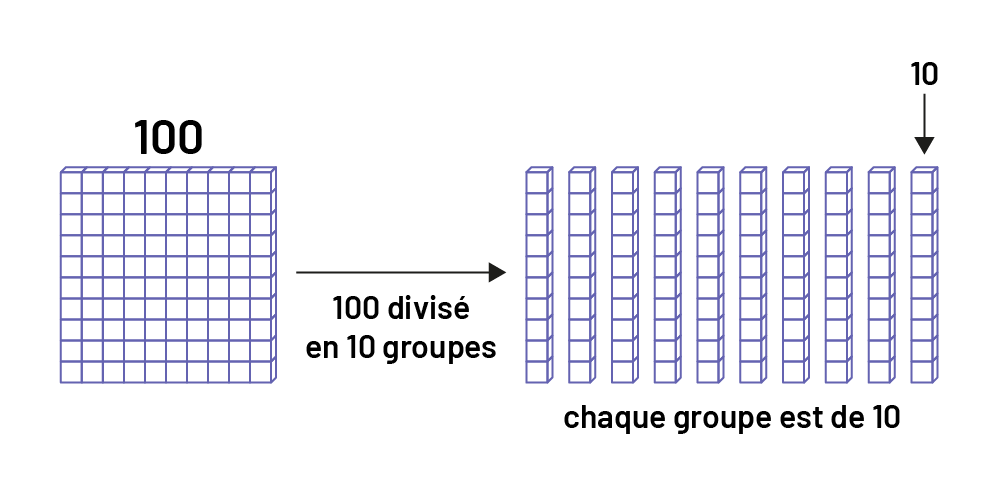
Une centaine divisée en 10 donne des groupes de 10.
 image
Une planchette de 100 au-dessus de laquelle est écrit le nombre 100.Une flèche part de la planchette et pointe vers un
groupe de dix réglettes de dix unités chacune. Au-dessous de la flèche on peut lire: 100 divisé en dix groupes.Le
nombre dix ainsi qu’une flèche partant de ce nombre et pointe vers l’une des réglettes.Sous le groupe de réglettes est
écrit: chaque groupe est de dix.
image
Une planchette de 100 au-dessus de laquelle est écrit le nombre 100.Une flèche part de la planchette et pointe vers un
groupe de dix réglettes de dix unités chacune. Au-dessous de la flèche on peut lire: 100 divisé en dix groupes.Le
nombre dix ainsi qu’une flèche partant de ce nombre et pointe vers l’une des réglettes.Sous le groupe de réglettes est
écrit: chaque groupe est de dix.
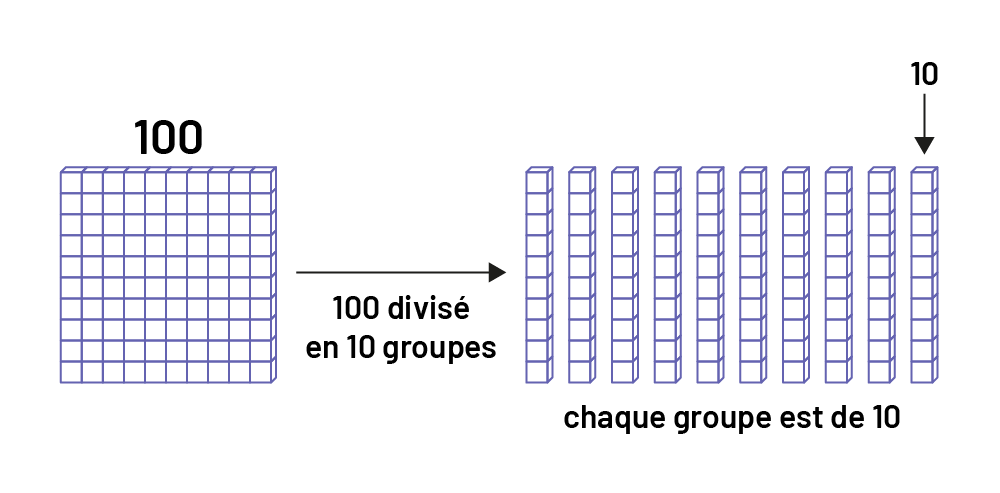
Une autre centaine divisée en 10 donne des groupes de 10.
 image
Une planchette de 100 au-dessus de laquelle est écrit le nombre 100.Une flèche part de la planchette et pointe vers un
groupe de dix réglettes de dix unités chacune. Au-dessous de la flèche on peut lire: 100 divisé en dix groupes.Le
nombre dix ainsi qu’une flèche partant de ce nombre et pointe vers l’une des réglettes.Sous le groupe de réglettes est
écrit: chaque groupe est de dix.
image
Une planchette de 100 au-dessus de laquelle est écrit le nombre 100.Une flèche part de la planchette et pointe vers un
groupe de dix réglettes de dix unités chacune. Au-dessous de la flèche on peut lire: 100 divisé en dix groupes.Le
nombre dix ainsi qu’une flèche partant de ce nombre et pointe vers l’une des réglettes.Sous le groupe de réglettes est
écrit: chaque groupe est de dix.
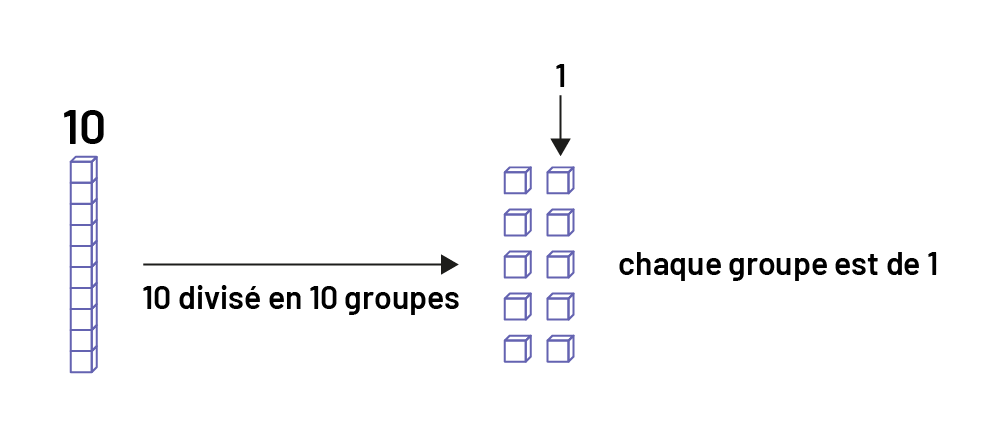
Une dizaine divisée en 10 donne des groupes de 1.
 image
Une réglette de dix unités au-dessus de laquelle est écrit le nombre dix. Une flèche part de la réglette et pointe dix
cubes individuels. Sous la flèche c’est écrit: dix divisé en dix groupes. Le chiffre un ainsi qu’une flèche partant de
ce chiffre et pointe vers l’un des dix cubes individuels. À droite de l’ensemble de cubes, on peut lire: chaque groupe
est de, un.
image
Une réglette de dix unités au-dessus de laquelle est écrit le nombre dix. Une flèche part de la réglette et pointe dix
cubes individuels. Sous la flèche c’est écrit: dix divisé en dix groupes. Le chiffre un ainsi qu’une flèche partant de
ce chiffre et pointe vers l’un des dix cubes individuels. À droite de l’ensemble de cubes, on peut lire: chaque groupe
est de, un.
Le quotient de la division \(210 \div 10\) est 21.
Les élèves doivent apprendre à maîtriser l’effet de la multiplication et de la division par des multiples de 10. L’explication de ces opérations se résume souvent à l’énoncé suivant : « Lorsqu’on multiplie par 10, on ajoute un zéro et lorsqu’on divise par 10, on enlève un zéro ». Cet énoncé est à déconseiller, car il ne tient pas compte de la compréhension des opérations et les élèves sont alors encouragés à appliquer un « truc » de façon mécanique.
Il est utile pour les élèves de reconnaître que des opérations comme \(5\; \times \;10\) ou \(130 \div 10\) peuvent être considérées comme \(5 \times 1\) dizaine, 13 dizaines ÷ 1 dizaine. On peut alors mieux comprendre l’apparition ou la disparition des chiffres « 0 » dans les opérations.
| Opération | Interprétation | Résultat |
|---|---|---|
|
\(5 \times 10\) |
\(5 \times 1\) dizaine      |
5 dizaines, c'est 50 |
|
\(130\; \div \;10\) |
130 séparé en groupes d'une dizaine              |
13 |
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 91-92.
Habileté : utiliser des stratégies de calcul mental pour additionner et soustraire des nombres décimaux jusqu’aux dixièmes, et expliquer les stratégies utilisées
Pour additionner efficacement des nombres décimaux, les élèves doivent comprendre la valeur de position des chiffres qui composent chacun des nombres et en tenir compte dans leurs calculs. Les élèves doivent aussi reconnaître que la virgule est un repère qui permet d’identifier la valeur de position des chiffres.
Lorsqu’on additionne des nombres décimaux, le concept de regroupement est utilisé tout comme lors de l’addition de nombres naturels. Par exemple, tout comme l’on peut ajouter 3 centaines à 8 centaines pour former 11 centaines, on peut ajouter 3 dixièmes à 8 dixièmes pour former 11 dixièmes. Or, puisque le système décimal ne permet pas d’inscrire deux chiffres dans une même position, les élèves doivent comprendre le concept de regroupement.
|
Centaines |
Dizaines |
Unités, |
Dixièmes |
|---|---|---|---|
|
0, |
3 |
||
|
0, |
8 |
||
|
1, |
1 |
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 98.
Au cours de la soustraction, il est important, comme il l’était dans le cas de l’addition, de tenir compte de la valeur de position des chiffres qui composent les nombres. Les stratégies pour soustraire les nombres décimaux sont essentiellement les mêmes que celles utilisées pour soustraire les nombres naturels.
L’élève peut conclure qu’un et un dixième est la même chose que onze dixièmes. À l’aide de mots, il est plus facile d’effectuer la soustraction de onze dixièmes moins huit dixièmes, qui donne 3 dixièmes.
 image
Tableau de valeur de position, centaines, dizaines, unités, dixièmes.Première ligne, une unité virgule un
dixième.Deuxième ligne, zéro unité et 8 dixièmes.Troisième ligne, zéro unité et 3 dixièmes.11 dixièmes moins 8
dixièmes égal 3 dixièmes.
image
Tableau de valeur de position, centaines, dizaines, unités, dixièmes.Première ligne, une unité virgule un
dixième.Deuxième ligne, zéro unité et 8 dixièmes.Troisième ligne, zéro unité et 3 dixièmes.11 dixièmes moins 8
dixièmes égal 3 dixièmes.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 101.
Calcul mental
La vie quotidienne présente de nombreuses occasions d’effectuer des opérations sur les nombres décimaux. Par exemple, les achats et les mesures font appel aux nombres décimaux. L’habileté à estimer et l’habileté à calculer mentalement sont des caractéristiques du sens du nombre et du sens des opérations. Diverses stratégies de calcul mental peuvent être utilisées dont l’arrondissement, la décomposition et la compensation, entre autres. Voici quelques exemples de leur utilisation en situation de calcul mental.
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 91.
Exemple 1
Annie veut savoir combien de bois acheter pour bâtir une niche pour son chien. La niche mesure :
1,2 m en hauteur
1,7 m en longueur
0,6 m en largeur
Estimation :
\(\begin{align}1,2 + 1,7 + 0,6 &\approx 1 + 2 + 1 \\ &\approx 4 \end{align}\)
Stratégie : Addition effectuée à l’aide de la compensation
Je sais que 0,8 + 0,2 = 1 alors je déplace mentalement 0,7 et 0,1 au 0,2. J’ai alors 2 unités, 1 unité et 5 dixièmes.
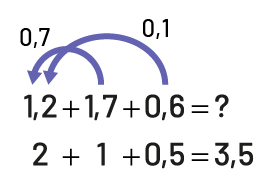 image
L’équation un, virgule 2 plus un, virgule 7 plus zéro virgule 6 égal inconnueUne flèche part du 7 et pointe le chiffre
un du nombre un virgule 2 pour montrer qu’on déplace mentalement le 7 dixièmes au nombre un, virgule 2. Une autre
flèche part du 6 et pointe le nombre un, virgule 2 pour montrer qu’on déplace mentalement un dixième au nombre un,
virgule 2.En deuxième ligne on peut voir l’équation:2 plus un plus zéro virgule 5 égal 3, virgule 5.
image
L’équation un, virgule 2 plus un, virgule 7 plus zéro virgule 6 égal inconnueUne flèche part du 7 et pointe le chiffre
un du nombre un virgule 2 pour montrer qu’on déplace mentalement le 7 dixièmes au nombre un, virgule 2. Une autre
flèche part du 6 et pointe le nombre un, virgule 2 pour montrer qu’on déplace mentalement un dixième au nombre un,
virgule 2.En deuxième ligne on peut voir l’équation:2 plus un plus zéro virgule 5 égal 3, virgule 5.
Stratégie : Addition effectuée à l’aide de la décomposition et la compensation
 image
Première ligne:Un, virgule 2 plus un, virgule 7 plus zéro, virgule 6 égal un plus un plus zéro, virgule 2 plus zéro,
virgule 7 plus zéro, virgule 6.Une flèche part du zéro, virgule 6 et pointe le zéro, virgule 7 pour montrer qu’on
déplace mentalement zéro, virgule un.Deuxième ligne: à partir du symbole égal, sont égal 2 plus zéro, virgule 2 plus
zéro, virgule 8 plus zéro, virgule 5.Troisième ligne, à partir du symbole égal, sont égal 2 plus un plus zéro, virgule
5.Quatrième ligne, à partir du symbole égal, sont égal 3, virgule 5.
image
Première ligne:Un, virgule 2 plus un, virgule 7 plus zéro, virgule 6 égal un plus un plus zéro, virgule 2 plus zéro,
virgule 7 plus zéro, virgule 6.Une flèche part du zéro, virgule 6 et pointe le zéro, virgule 7 pour montrer qu’on
déplace mentalement zéro, virgule un.Deuxième ligne: à partir du symbole égal, sont égal 2 plus zéro, virgule 2 plus
zéro, virgule 8 plus zéro, virgule 5.Troisième ligne, à partir du symbole égal, sont égal 2 plus un plus zéro, virgule
5.Quatrième ligne, à partir du symbole égal, sont égal 3, virgule 5.
Exemple 2
La chienne de Casimir a donné naissance à 2 chiots. La vétérinaire explique que les chiots doivent peser au moins 24,7 kg lorsqu’ils ont six mois pour être en bonne santé. Casimir veut savoir combien de poids chaque chiot doit prendre. Le premier chiot pèse 3,8 kg et le deuxième chiot pèse 4,4 kg.
Estimation :
Chiot 1 : \(\begin{align}24,7 - 3,8 &\approx 25 - 4\\ &\approx 21 \end{align}\)
Chiot 2 : \(\begin{align}24,7 - 4,4 &\approx 25 - 4\\ &\approx 21 \end{align}\)
Stratégie : Soustraction effectuée à l’aide de la décomposition
Je décompose mentalement chaque terme en unités et en dixièmes.
\(\begin{align} 24,7 - 3,8 &= (23 - 3) + (1,7 - 0,8) \\ &= \; 20 + 0,9 \\ &= \; 20,9 \;\;\; kg \end{align}\)
\(\begin{align}24,7 - 4,4 &= (24 - 4) + (0,7 - 0,4) \\ &= \; 20 + 0,3 \\ &= \; 20,3\;\;kg \end{align}\)
La masse de chiot 1 doit augmenter de 20,9 kg.
La masse de chiot 2 doit augmenter de 20,3 kg.
Stratégie : Compensation à l’aide de la droite numérique
Chiot 1 :
J’identifie 24,7 et 3,8 sur ma droite et je représente la distance entre les deux nombres à l’aide d’un rectangle. Afin de faciliter la soustraction, je déplace mentalement mon rectangle vers la gauche à 3 au lieu de 3,8. Mon rectangle est donc déplacé de 0,8 des deux côtés. Puisque la grandeur de mon rectangle reste inchangée, c’est-à-dire l’écart reste pareil, la fin de celui-ci est maintenant à 23,9. Ma soustraction devient \(\ 23,9 - 3\).
 image Une droite numérique non graduée sur laquelle 2 rectangles
mauves de même longueur sont posés. Le premier rectangle ayant l’inscription 24, virgule 7 moins 3, virgule 8 est
posé sur la droite entre les tirets indiquant 3, virgule 8 et 24, virgule 7.Le deuxième rectangle au-dessus du
premier porte l’inscription 23, virgule 9 moins 3. Ce rectangle commence vis-à-vis du tiret indiquant le nombre 3 et
se termine au tiret indiquant le nombre 23, virgule 9.Sous le rectangle on peut lire les 3 lignes suivantes:Ligne
un: 24, virgule 7 moins 3, virgule 8 égal (parenthèse ouvrante) 24, virgule 7 moins zéro, virgule 8 (parenthèse
fermante) moins (parenthèse ouvrante) 3, virgule 8 moins zéro, virgule 8 (parenthèse fermante)Ligne 2: à partir du
symbole égal, sont égal 23, virgule 9 moins 3Ligne 3: à partir du symbole égal, sont égal 20, virgule 9
kilogrammes.
image Une droite numérique non graduée sur laquelle 2 rectangles
mauves de même longueur sont posés. Le premier rectangle ayant l’inscription 24, virgule 7 moins 3, virgule 8 est
posé sur la droite entre les tirets indiquant 3, virgule 8 et 24, virgule 7.Le deuxième rectangle au-dessus du
premier porte l’inscription 23, virgule 9 moins 3. Ce rectangle commence vis-à-vis du tiret indiquant le nombre 3 et
se termine au tiret indiquant le nombre 23, virgule 9.Sous le rectangle on peut lire les 3 lignes suivantes:Ligne
un: 24, virgule 7 moins 3, virgule 8 égal (parenthèse ouvrante) 24, virgule 7 moins zéro, virgule 8 (parenthèse
fermante) moins (parenthèse ouvrante) 3, virgule 8 moins zéro, virgule 8 (parenthèse fermante)Ligne 2: à partir du
symbole égal, sont égal 23, virgule 9 moins 3Ligne 3: à partir du symbole égal, sont égal 20, virgule 9
kilogrammes.
\(\begin{align}24,7 - 3,8 &= (24,7 - 0,8) - (3,8 - 0,8)\\ &= 23,9 - 3\\ &= 20,9\;\;{\rm{kg}} \end{align}\)
Il est beaucoup plus facile d’enlever 3 unités de 23,9.
\(\ 23,9 - 3 = 20,9\)
La masse de chiot 1 doit augmenter de 20,9 kg.
Exemple 3
Dans cette vidéo, les élèves réfléchissent, partagent et développent différentes stratégies de calcul mental en lien avec l'addition de nombres décimaux.
 Description de la vidéo
Description de la vidéo
Description à venir
