B2.4 Représenter et résoudre des problèmes relatifs à l’addition de nombres naturels dont la somme est égale ou inférieure à 10 000 et à la soustraction de nombres naturels égaux ou inférieurs à 10 000 ainsi qu’à l’addition et à la soustraction de nombres décimaux jusqu’aux dixièmes, à l’aide d’outils et de stratégies appropriés, et d’algorithmes.
Habileté : représenter et résoudre des problèmes relatifs à l’addition et à la soustraction à l’aide de stratégies y compris des algorithmes
L’apprentissage des opérations mathématiques s’effectue progressivement. Le point de départ devrait être l’exploration des opérations en situation de résolution de problèmes. Les élèves apprennent à associer des situations à des opérations particulières, ce qui leur permet de commencer à donner un sens aux opérations. De plus, les élèves doivent utiliser des stratégies basées sur leur compréhension du contexte, du problème et des opérations. Les élèves prennent conscience qu’il existe plusieurs façons de résoudre un problème et même plusieurs façons d’effectuer la même opération. Par la suite, les élèves sont invités à résoudre une variété de problèmes afin de progresser vers l’utilisation de stratégies efficaces.
Contrairement à la démarche traditionnelle où les élèves apprennent surtout à appliquer les algorithmes usuels, l’apprentissage des opérations doit davantage être orienté vers la compréhension des opérations, l’exploration du calcul mental et l’utilisation de diverses stratégies pour effectuer les opérations.
Pour développer des stratégies efficaces chez les élèves, il est important d’offrir aux élèves divers types de problèmes de manière à leur permettre de saisir les multiples sens des opérations. Un problème bien choisi et l’application d’une stratégie réfléchie sont plus profitables qu’une série d’exercices complétés mécaniquement. Il faut ainsi allouer le temps nécessaire qui permettra aux élèves de comprendre et de consolider les stratégies.
Problèmes écrits : Addition et soustraction
Dans l’addition ou la soustraction, des quantités sont ajoutées, retirées, unies ou comparées. Pour que les élèves comprennent les liens entre les quantités dans chacun de ces cas, il est important qu’elles et ils soient confrontés à divers types de problèmes.
L’addition et la soustraction ne sont que des opérations qui surviennent dans des problèmes. Il faut donc éviter de parler de « problèmes de soustraction » ou « problèmes d’addition », car c’est la compréhension de la situation, ainsi que la compréhension des opérations qui font choisir la stratégie de résolution de problèmes à adopter, en l’occurrence le choix de l’addition ou de la soustraction. Donc, les élèves doivent analyser le problème, choisir une stratégie et l’appliquer, tout comme le font les adultes. Dans ce contexte, le rôle du personnel enseignant est d’aider les élèves dans leur analyse et dans leur compréhension des opérations.
Il est important de noter que les problèmes présentés ci-dessous semblent similaires en raison de leur contexte. Or pour les élèves, chaque situation représente un problème particulier. C’est en maîtrisant ces divers types de problèmes que les élèves acquièrent une maîtrise de l’addition et de la soustraction.
Problèmes d’ajout
Le modèle partie-tout peut être utile pour représenter les valeurs connues et inconnues dans des problèmes d’ajout. Le modèle d’ensemble est utile pour représenter l’ajout d’une quantité.
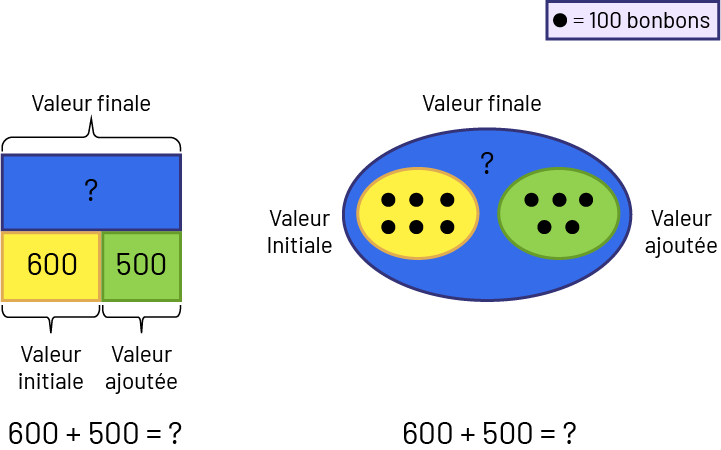
- Ajout : Valeur finale inconnue – Jamil a un sac de 600 bonbons. Il achète 500 bonbons de plus. Combien de bonbons Jamil a-t-il à présent?
 Image
un: 600 plus 500 égal point d’interrogation.Un rectangle bleu identifié avec un point d’interrogation au-dessus duquel
un crochet représente la valeur finale.Sous le rectangle il y a 2 rectangles qui, ensemble, occupent le même espace
que le rectangle bleu.Le rectangle de gauche est jaune et il y est inscrit le nombre 600. Un crochet sous le rectangle
jaune indique que c’est la valeur initiale.Le rectangle de droite est vert et il y est inscrit 500. Un crochet sous le
rectangle vert indique que c’est la valeur ajoutée.Image 2: 600 plus 500 égal point d’interrogation.Une légende décrit
que chaque point noir vaut 100 bonbons.Un ensemble bleu contient un ensemble jaune et un ensemble vert. L’ensemble
jaune est identifié comme la valeur initiale.Dans l’ensemble jaune, il y a 6 points noirs. L’ensemble vert est
identifié comme la valeur ajoutée.Dans l’ensemble vert il y a 5 points noirs.Dans le cercle bleu représentant la
valeur finale, il y a un point d’interrogation.
Image
un: 600 plus 500 égal point d’interrogation.Un rectangle bleu identifié avec un point d’interrogation au-dessus duquel
un crochet représente la valeur finale.Sous le rectangle il y a 2 rectangles qui, ensemble, occupent le même espace
que le rectangle bleu.Le rectangle de gauche est jaune et il y est inscrit le nombre 600. Un crochet sous le rectangle
jaune indique que c’est la valeur initiale.Le rectangle de droite est vert et il y est inscrit 500. Un crochet sous le
rectangle vert indique que c’est la valeur ajoutée.Image 2: 600 plus 500 égal point d’interrogation.Une légende décrit
que chaque point noir vaut 100 bonbons.Un ensemble bleu contient un ensemble jaune et un ensemble vert. L’ensemble
jaune est identifié comme la valeur initiale.Dans l’ensemble jaune, il y a 6 points noirs. L’ensemble vert est
identifié comme la valeur ajoutée.Dans l’ensemble vert il y a 5 points noirs.Dans le cercle bleu représentant la
valeur finale, il y a un point d’interrogation.
- Ajout : Valeur initiale inconnue – Jamil a plusieurs bonbons. Il en achète 500 de plus. Il en a 1 100 à présent. Combien de bonbons Jamil avait-il au début?
 image Point d’interrogation plus 500 égal 1100.Un rectangle bleu identifié avec le nombre 1100
au-dessus duquel un crochet représente la valeur finale.Sous le rectangle il y a 2 rectangles qui, ensemble, occupent
le même espace que le rectangle bleu.Le rectangle de gauche est jaune et il y est inscrit un point d'interrogation. Un
crochet sous le rectangle jaune indique que c’est la valeur initiale.Le rectangle de droite est vert et il y est
inscrit le nombre 500. Un crochet sous le rectangle vert indique que c’est la valeur ajoutée.
image Point d’interrogation plus 500 égal 1100.Un rectangle bleu identifié avec le nombre 1100
au-dessus duquel un crochet représente la valeur finale.Sous le rectangle il y a 2 rectangles qui, ensemble, occupent
le même espace que le rectangle bleu.Le rectangle de gauche est jaune et il y est inscrit un point d'interrogation. Un
crochet sous le rectangle jaune indique que c’est la valeur initiale.Le rectangle de droite est vert et il y est
inscrit le nombre 500. Un crochet sous le rectangle vert indique que c’est la valeur ajoutée.
- Ajout : Valeur ajoutée inconnue – Jamil a un sac de 600 bonbons. Il en achète beaucoup d’autres. Il en a 1 100 à présent. Combien de bonbons Jamil a-t-il achetés?
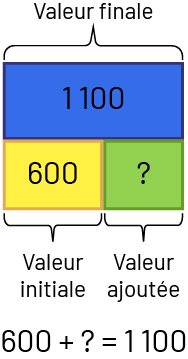 image 600 plus point d’interrogation égal 1100.Un rectangle bleu identifié avec le nombre 1100
au-dessus duquel un crochet représente la valeur finale.Sous le rectangle il y a 2 rectangles qui, ensemble, occupent
le même espace que le rectangle bleu.Le rectangle de gauche est jaune et il y est inscrit le nombre 600. Un crochet
sous le rectangle jaune indique que c’est la valeur initiale.Le rectangle de droite est vert et il y est inscrit un
point d’interrogation. Un crochet sous le rectangle vert indique que c’est la valeur ajoutée.
image 600 plus point d’interrogation égal 1100.Un rectangle bleu identifié avec le nombre 1100
au-dessus duquel un crochet représente la valeur finale.Sous le rectangle il y a 2 rectangles qui, ensemble, occupent
le même espace que le rectangle bleu.Le rectangle de gauche est jaune et il y est inscrit le nombre 600. Un crochet
sous le rectangle jaune indique que c’est la valeur initiale.Le rectangle de droite est vert et il y est inscrit un
point d’interrogation. Un crochet sous le rectangle vert indique que c’est la valeur ajoutée.
Problèmes de retrait
Le modèle partie-tout peut être utile pour représenter les valeurs connues et inconnues dans des problèmes de retrait. Le modèle d’ensemble est utile pour représenter le retrait d’une quantité.
- Retrait : Valeur finale inconnue – Nadia a 1 500 $. Elle donne 500 $ à son frère. Combien lui reste-t-il de dollars à présent?
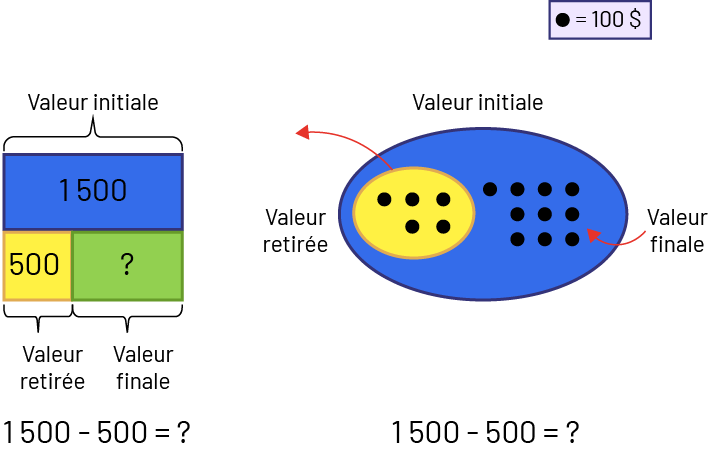 Image
un:1500 moins 500 égal point d’interrogation.Un rectangle bleu identifié avec le nombre 1500 au-dessus duquel un
crochet représente la valeur initiale.Sous le rectangle il y a 2 rectangles qui, ensemble, occupent le même espace que
le rectangle bleu.Le rectangle de gauche est jaune et il y est inscrit le nombre 500. Un crochet sous le rectangle
jaune indique que c’est la valeur retirée.Le rectangle de droite est vert et il y est inscrit un point
d’interrogation. Un crochet sous le rectangle vert indique que c’est la valeur finale.Image 2: 1500 moins 500 égal
point d’interrogation.Une légende indique qu’un point noir équivaut à 100 dollars.Un grand ensemble bleu correspond à
la valeur initiale.Dans l’ensemble bleu, 6 points noirs font partie d’un ensemble jaune représentant la valeur
retirée. Une flèche rouge part de cette direction et pointe en dehors de l’ensemble bleu.À côté de l’ensemble jaune,
dans l’ensemble bleu, il y a dix points noirs représentant la valeur finale. Une flèche rouge partant de l’extérieur
de l’ensemble bleu et pointant vers l’ensemble de dix points noirs dans l’ensemble bleu.
Image
un:1500 moins 500 égal point d’interrogation.Un rectangle bleu identifié avec le nombre 1500 au-dessus duquel un
crochet représente la valeur initiale.Sous le rectangle il y a 2 rectangles qui, ensemble, occupent le même espace que
le rectangle bleu.Le rectangle de gauche est jaune et il y est inscrit le nombre 500. Un crochet sous le rectangle
jaune indique que c’est la valeur retirée.Le rectangle de droite est vert et il y est inscrit un point
d’interrogation. Un crochet sous le rectangle vert indique que c’est la valeur finale.Image 2: 1500 moins 500 égal
point d’interrogation.Une légende indique qu’un point noir équivaut à 100 dollars.Un grand ensemble bleu correspond à
la valeur initiale.Dans l’ensemble bleu, 6 points noirs font partie d’un ensemble jaune représentant la valeur
retirée. Une flèche rouge part de cette direction et pointe en dehors de l’ensemble bleu.À côté de l’ensemble jaune,
dans l’ensemble bleu, il y a dix points noirs représentant la valeur finale. Une flèche rouge partant de l’extérieur
de l’ensemble bleu et pointant vers l’ensemble de dix points noirs dans l’ensemble bleu.
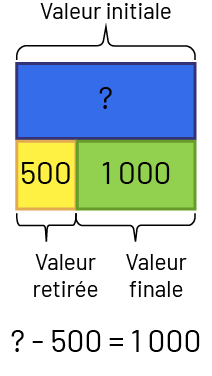
- Retrait : Valeur retirée inconnue – Nadia a 1 500 $. Elle en donne à son frère. Il lui reste 1 000 $ à présent. Combien d’argent Nadia a-t-elle donné à son frère?
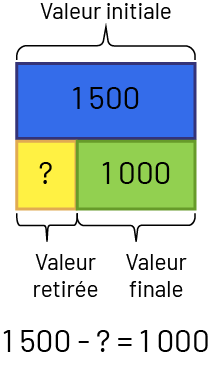 image 1500 moins point d’interrogation égal 1000.Un rectangle bleu identifié avec le nombre 1500
au-dessus duquel un crochet représente la valeur initiale.Sous le rectangle il y a 2 rectangles qui, ensemble,
occupent le même espace que le rectangle bleu.Le rectangle de gauche est jaune et il y est inscrit un point
d’interrogation. Un crochet sous le rectangle jaune indique que c’est la valeur retirée.Le rectangle de droite est
vert et il y est inscrit le nombre 1000. Un crochet sous le rectangle vert indique que c’est la valeur finale.
image 1500 moins point d’interrogation égal 1000.Un rectangle bleu identifié avec le nombre 1500
au-dessus duquel un crochet représente la valeur initiale.Sous le rectangle il y a 2 rectangles qui, ensemble,
occupent le même espace que le rectangle bleu.Le rectangle de gauche est jaune et il y est inscrit un point
d’interrogation. Un crochet sous le rectangle jaune indique que c’est la valeur retirée.Le rectangle de droite est
vert et il y est inscrit le nombre 1000. Un crochet sous le rectangle vert indique que c’est la valeur finale.
- Retrait : Valeur initiale inconnue – Nadia avait un certain montant d’argent. Elle a donné 500 $ à son frère. Il lui reste 1 000 $ à présent. Combien Nadia avait-elle d’argent au début?
Problèmes de réunion
Le modèle partie-tout peut être utile pour représenter les parties du tout connues et inconnues ou le tout connu ou inconnu dans des problèmes de réunion.
- Réunion : Partie du tout inconnue – La classe a 800 crayons de couleur, et 300 de ces crayons sont rouges. Les crayons qui restent sont bleus. Combien la classe a-t-elle de crayons bleus?
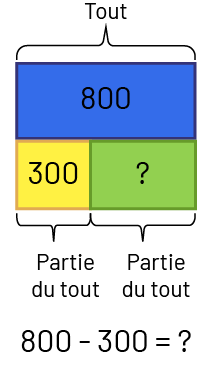 image 800 moins 300 égal point d’interrogation. Un rectangle bleu identifié avec le nombre 800
au-dessus duquel un crochet représente le tout. Sous le rectangle il y a 2 rectangles qui, ensemble, occupent le même
espace que le rectangle bleu. Le rectangle de gauche est jaune et il y est inscrit le nombre 300. Un crochet sous le
rectangle jaune indique que c’est une partie du tout. Le rectangle de droite est vert et il y est inscrit un point
d’interrogation. Un crochet sous le rectangle vert indique que c’est une partie du tout.
image 800 moins 300 égal point d’interrogation. Un rectangle bleu identifié avec le nombre 800
au-dessus duquel un crochet représente le tout. Sous le rectangle il y a 2 rectangles qui, ensemble, occupent le même
espace que le rectangle bleu. Le rectangle de gauche est jaune et il y est inscrit le nombre 300. Un crochet sous le
rectangle jaune indique que c’est une partie du tout. Le rectangle de droite est vert et il y est inscrit un point
d’interrogation. Un crochet sous le rectangle vert indique que c’est une partie du tout.
- Réunion : Tout inconnu – La classe a beaucoup de crayons de couleur. Il y a 300 crayons rouges et 500 crayons bleus. Combien la classe a-t-elle de crayons de couleur?
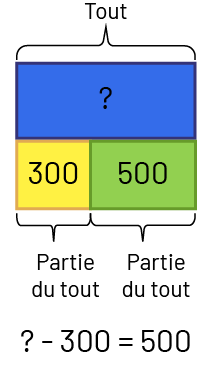 image Point d’interrogation moins 300 égal 500.Un rectangle bleu identifié avec un point
d’interrogation au-dessus duquel un crochet représente le tout.Sous le rectangle il y a 2 rectangles qui, ensemble,
occupent le même espace que le rectangle bleu.Le rectangle de gauche est jaune et il y est inscrit le nombre 300. Un
crochet sous le rectangle jaune indique que c’est une partie du tout.Le rectangle de droite est vert et il y est
inscrit le nombre 500. Un crochet sous le rectangle vert indique que c’est une partie du tout.
image Point d’interrogation moins 300 égal 500.Un rectangle bleu identifié avec un point
d’interrogation au-dessus duquel un crochet représente le tout.Sous le rectangle il y a 2 rectangles qui, ensemble,
occupent le même espace que le rectangle bleu.Le rectangle de gauche est jaune et il y est inscrit le nombre 300. Un
crochet sous le rectangle jaune indique que c’est une partie du tout.Le rectangle de droite est vert et il y est
inscrit le nombre 500. Un crochet sous le rectangle vert indique que c’est une partie du tout.
Problèmes de comparaison
Le modèle linéaire peut être utile pour représenter la différence entre deux nombres dans des problèmes de comparaison. Dans cet exemple, on utilise les réglettes Cuisenaire et la droite numérique double.
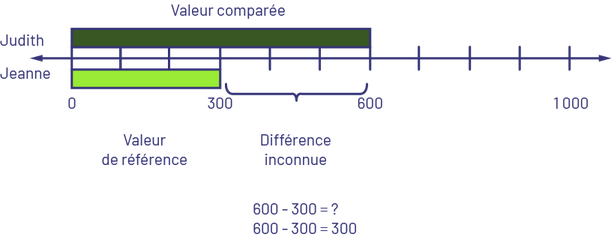
- Comparaison : Différence inconnue – Judith a 600 $ et Jeanne a 300 $. Combien de dollars Judith a-t-elle de plus que Jeanne? OU Judith a 600 $ et Jeanne a 300 $. Combien de dollars Jeanne a-t-elle de moins que Judith?
Je sais que la réglette vert foncé représente 6 (centaines), alors je la place en haut de la droite numérique en partant du 0. Je sais que la réglette vert lime représente 3 (centaines), alors je la place sous la droite numérique en partant du 0. Je compare les deux réglettes et je vois que la réglette vert lime est 3 (centaines) de moins que la réglette vert foncé. Je trouve la différence ou l’écart entre les deux quantités. Il y a une différence de 300 $. Judith a 300 $ de plus que Jeanne ou Jeanne a 300 $ de moins que Judith.
 image
Une droite numérique graduée de zéro à 1000 par intervalles de 100.Une réglette vert foncé intitulée valeur comparée
est posée sur le dessus de la droite et attribué à Judith. Cette réglette part de zéro et se rend jusqu’au tiret
identifié par 600.Une réglette, vert lime, intitulée valeur de référence est sous la droite et est attribuée à Jeanne.
Cette réglette part de zéro et se rend jusqu’au tiret identifié par 300. Un crochet reliant l'intervalle entre 300 et
600 est intitulé Différence connue.600 moins 300 égal point d’interrogation600 moins 300 égal 300.
image
Une droite numérique graduée de zéro à 1000 par intervalles de 100.Une réglette vert foncé intitulée valeur comparée
est posée sur le dessus de la droite et attribué à Judith. Cette réglette part de zéro et se rend jusqu’au tiret
identifié par 600.Une réglette, vert lime, intitulée valeur de référence est sous la droite et est attribuée à Jeanne.
Cette réglette part de zéro et se rend jusqu’au tiret identifié par 300. Un crochet reliant l'intervalle entre 300 et
600 est intitulé Différence connue.600 moins 300 égal point d’interrogation600 moins 300 égal 300.
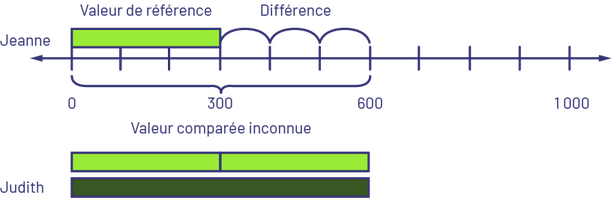
- Comparaison : Valeur comparée inconnue – Judith a 300 $ de plus que Jeanne. Jeanne a 300 $. Combien de dollars Judith at-elle? OU Jeanne a 300 $ de moins que Judith. Jeanne a 300 $. Combien de dollars Judith a-t-elle?
Je sais que la réglette vert lime représente 3 (centaines), alors je la place en haut de la droite numérique en partant du 0. Je prends une autre réglette vert lime et je la place sous la droite numérique en partant du 0 et j’ajoute une autre réglette vert lime puisque Judith a 300 $ de plus que Jeanne. Je remplace les deux réglettes vert lime avec la réglette vert foncé qui représente 6 (centaines). Judith a donc 600 $.
 image
Une droite numérique graduée de zéro à 1000 par intervalles de 100.Une réglette vert foncé intitulée valeur comparée
est posée sur le dessus de la droite et attribué à Judith. Cette réglette part de zéro et se rend jusqu’au tiret
identifié par 600.Une réglette, vert lime, intitulée valeur de référence est sous la droite et est attribuée à Jeanne.
Cette réglette part de zéro et se rend jusqu’au tiret identifié par 300. Un crochet reliant l'intervalle entre 300 et
600 est intitulé Différence connue.600 moins 300 égal point d’interrogation600 moins 300 égal 300.
image
Une droite numérique graduée de zéro à 1000 par intervalles de 100.Une réglette vert foncé intitulée valeur comparée
est posée sur le dessus de la droite et attribué à Judith. Cette réglette part de zéro et se rend jusqu’au tiret
identifié par 600.Une réglette, vert lime, intitulée valeur de référence est sous la droite et est attribuée à Jeanne.
Cette réglette part de zéro et se rend jusqu’au tiret identifié par 300. Un crochet reliant l'intervalle entre 300 et
600 est intitulé Différence connue.600 moins 300 égal point d’interrogation600 moins 300 égal 300.
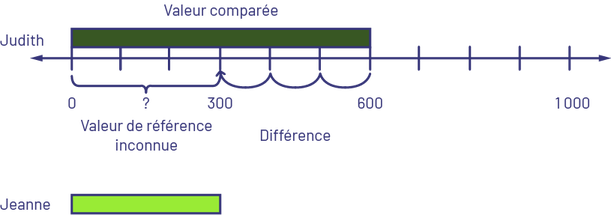
- Comparaison : Valeur de référence inconnue – Judith a 600 $ et Jeanne a 300 $ de moins que Judith. Combien de dollars Jeanne a-t-elle? ou Jeanne a 300 $ de moins que Judith. Judith a 600 $. Combien de dollars Jeanne a-t-elle?
Je sais que la réglette vert foncé représente 6 (centaines), alors je la place en haut de la droite numérique en partant du 0. Sur la droite numérique, je compte à rebours de trois bonds pour arriver à 300 pour représenter que Jeanne a 300 $ de moins que Judith. Je prends une réglette vert lime, qui représente 3 (centaines) et je la place sous la droite numérique en partant du 0. Jeanne a 300 $.
 image
Une droite numérique graduée de zéro à 1000 par intervalles de 100.Une réglette vert foncé intitulée valeur comparée
est posée sur le dessus de la droite et attribué à Judith. Cette réglette part de zéro et se rend jusqu’au tiret
identifié par 600.Un crochet reliant les tirets zéro et 300 est identifié avec un point d’interrogation. Ce crochet
signifie la valeur de référence inconnue. Trois bonds partent de 600 vers 500, de 500 vers 400 et de 400 vers 300. Ces
bonds sont identifiés comme étant la différence.Image 2: une réglette vert lime identifiée comme Jeanne ayant la
longueur de l’intervalle zéro à 300 de la droite de l’image un.
image
Une droite numérique graduée de zéro à 1000 par intervalles de 100.Une réglette vert foncé intitulée valeur comparée
est posée sur le dessus de la droite et attribué à Judith. Cette réglette part de zéro et se rend jusqu’au tiret
identifié par 600.Un crochet reliant les tirets zéro et 300 est identifié avec un point d’interrogation. Ce crochet
signifie la valeur de référence inconnue. Trois bonds partent de 600 vers 500, de 500 vers 400 et de 400 vers 300. Ces
bonds sont identifiés comme étant la différence.Image 2: une réglette vert lime identifiée comme Jeanne ayant la
longueur de l’intervalle zéro à 300 de la droite de l’image un.
Source : Guide d'enseignement efficace des mathématiques de la maternelle à la 6e année, p. 8-10.
Les problèmes d’ajout et de retrait sont perçus par les élèves comme des situations actives, plus faciles à modéliser et à « voir », car la quantité initiale augmente ou diminue. Les problèmes de réunion, cependant, supposent une situation statique, car aucune action ou aucun changement ne se produit, ce qui les rend plus abstraits et plus difficiles à comprendre. Les problèmes de comparaison, quant à eux, traitent de la relation entre deux quantités en les opposant : il n’y a donc pas d’action, mais une comparaison d’une quantité à une autre.
Puisque les élèves sont exposés régulièrement à des problèmes dont la quantité finale est recherchée, elles et ils les résolvent plus aisément. Cependant, elles et ils ont plus de mal à résoudre les problèmes dont l’inconnue est la quantité initiale, la quantité ajoutée ou la quantité retirée. Ces problèmes aident à développer une compréhension plus solide des opérations d’addition et de soustraction et des liens entre les opérations. Par exemple, dans le cas des problèmes d’ajout dont l’inconnue est la quantité initiale, les élèves voient plus facilement les avantages de l’addition (par exemple, \(?\; + \;12\; = \;37\)) qui permet de respecter l’ordre dans lequel se déroule l’action dans le problème. Cela leur permet d’utiliser une stratégie (par exemple, dénombrement ou compte à rebours) afin de déterminer la quantité initiale. Ces élèves démontrent leur compréhension du problème et leur habileté à utiliser une stratégie pour le résoudre. Cependant, elles et ils ne démontrent pas une compréhension du sens de la différence (et de la soustraction). Si elles et ils avaient utilisé la soustraction, soit \(37\; - \;12\; = \;?\), elles et ils auraient démontré une compréhension plus élargie des liens entre les quantités par rapport à cette opération. Mais lorsque les élèves sont en apprentissage, il est inutile de leur imposer une stratégie.
L’obligation de soustraire n’aidera en rien les élèves qui ne voient pas la pertinence de cette stratégie. Toutefois, si elles et ils sont régulièrement en contact avec une variété de problèmes et qu’elles et ils participent aux échanges mathématiques qui suivent, elles et ils arrivent à voir les liens entre diverses stratégies et à assimiler une variété de stratégies.
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 81-84.
Stratégies de calculs
Les stratégies personnelles ou inventées offrent plusieurs avantages par rapport à l’enseignement traditionnel des algorithmes usuels, à commencer par la fierté et la confiance en soi qu’elles procurent. Les élèves qui utilisent des algorithmes personnels font moins d’erreurs, car elles et ils comprennent ce qui est fait. De plus, les élèves améliorent leur connaissance et leur compréhension du système numérique à base dix, sur lequel reposent la plupart des stratégies de calcul.
Par ailleurs, Van de Walle et Lovin (2006, p. 40) précisent que des recherches démontrent que les élèves qui ont pu développer des stratégies personnelles réussissent aussi bien, sinon mieux, que les autres dans des tests standardisés.
Il existe des disparités de taille entre les algorithmes personnels et les algorithmes usuels. Les algorithmes personnels sont habituellement orientés sur le sens des chiffres, selon leur position (par exemple, dans l’addition 323 + 20, j’ajoute 2 dizaines à 323, ce qui donne 343) alors que les algorithmes usuels tendent à utiliser les chiffres sans tenir compte de leur position (par exemple, dans l’addition \(323\; + \;20\), on fait : \(3\; + \;0\), c’est 3; \(2\; + \;2\), c’est 4…).
Les algorithmes usuels commencent habituellement par la droite, alors que dans leurs algorithmes personnels, les élèves commencent souvent par la gauche, ce qui leur permet de maintenir un sens de la grandeur des quantités en cause. Puisqu’un algorithme personnel est le fruit de l’imagination et de la compréhension de chaque élève, il demeure très souple, de manière qu’il puisse servir dans diverses situations.
En salle de classe, il est suggéré d’examiner plusieurs algorithmes pour une même opération. Il est essentiel que les élèves comprennent le raisonnement derrière les gestes posés dans ces algorithmes. Avec le temps, cela leur permet de choisir une stratégie efficace selon le contexte. Le personnel enseignant qui a dans sa classe des élèves de cultures différentes peut les inviter à discuter, à la maison, de la méthode que les parents utilisent pour effectuer une addition, une soustraction, une multiplication ou une division. Ces élèves peuvent présenter ces méthodes à la classe, ce qui peut apporter de nouvelles stratégies.
On présente souvent les algorithmes usuels comme principale stratégie de calcul. Bien qu’ils soient efficaces, ils ne sont pas toujours appropriés. Lorsque l’enseignement est axé sur l’algorithme usuel, par exemple, pour calculer \(300\; - \;15\), les élèves ont tendance à sortir un crayon et à résoudre le problème par écrit, avec l’algorithme écrit et ses échanges, ce qui est une source commune d’erreurs. Il est pourtant plus efficace de calculer mentalement comme suit : \(300\; - \;10\; = \;290,\;290\; - \;5\; = \;285\). De plus, l’algorithme usuel n’est pas la meilleure méthode à utiliser là où une estimation suffit. C’est pourquoi il est suggéré de considérer l’algorithme usuel comme une stratégie de calcul parmi tant d’autres.
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 118-119.
Les élèves peuvent résoudre des problèmes écrits de différentes façons. Les tableaux qui suivent donnent quelques exemples d’algorithmes d’additions et de soustractions. Ce ne sont pas les seules façons de résoudre un problème, il en existe beaucoup d’autres, aussi faut-il donner aux élèves des occasions de raisonner pour découvrir d’autres façons de faire.
Voici des algorithmes que peuvent utiliser les élèves pour déterminer la somme 566 + 379 = _.
Il en existe d'autres et ils varieront dans chaque groupe-classe.
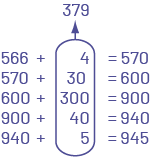
L'élève procède par étapes et décompose le dernier nombre seulement.
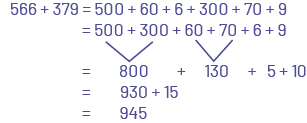
L'élève décompose horizontalement les nombres.
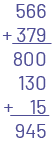
L'élève regroupe les centaines, les dizaines et les unités.
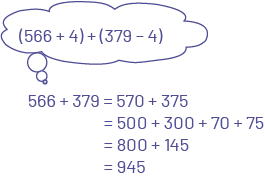
L'élève utlise une technique de compensation.
Voici des exemples d'algorithmes que peuvent utiliser les élèves pour déterminer la différence 631 - 439 = _ et l'expliquer. Il en existe d'autres et ils varieront dans chaque groupe-classe.
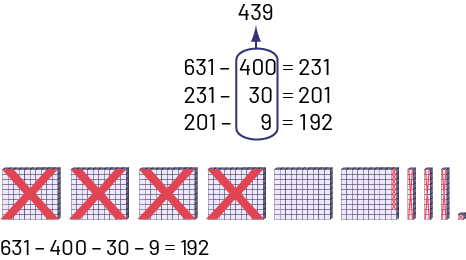 image 3 soustractions sont superposées.631 moins 400 égal 231.231 moins 30 égal 201.201 moins 9
égal 192.Tous les deuxièmes nombres des soustractions sont encerclés et additionnés pour un total de 439.Dix
blocs de centaines sont alignés.4 d’entre eux sont marqués d’une croix rouge.3 colonnes de dix sont marquées
d’une croix rouge ainsi que neuf blocs d’unités.Une soustraction :631 moins 400 moins 30 moins, 9 égal
192.
image 3 soustractions sont superposées.631 moins 400 égal 231.231 moins 30 égal 201.201 moins 9
égal 192.Tous les deuxièmes nombres des soustractions sont encerclés et additionnés pour un total de 439.Dix
blocs de centaines sont alignés.4 d’entre eux sont marqués d’une croix rouge.3 colonnes de dix sont marquées
d’une croix rouge ainsi que neuf blocs d’unités.Une soustraction :631 moins 400 moins 30 moins, 9 égal
192.
L'élève décompose le second terme et soustrait par étapes.
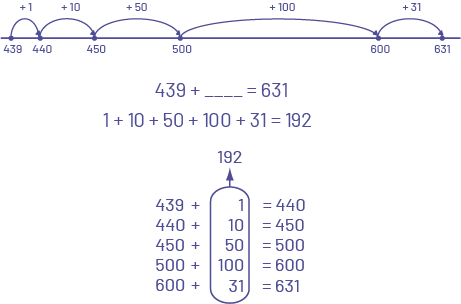 image Droite numérique de 439 à 631, sans intervalle
régulier. Des flèches représentent des bonds :-de 439 à 440, un bond de plus un.-de 440 à 450, un bond de plus
dix.-de 450 à 500, un bond de plus 50.-de 500 à 600, un bond de plus 100.-de 600 à 631, un bond de plus 31.439
plus combien est égal à 631.Un plus dix plus 50 plus 100 plus 31 égal 192.Des phrases numériques sont
superposées :439 plus 1 égal 440.440 plus 10 égal 450.450 plus 50 égal 500.500 plus 100 égal 600.600 plus 31
égal 631.Tous les deuxièmes nombres sont encerclés, et additionnés pour un total de 192.
image Droite numérique de 439 à 631, sans intervalle
régulier. Des flèches représentent des bonds :-de 439 à 440, un bond de plus un.-de 440 à 450, un bond de plus
dix.-de 450 à 500, un bond de plus 50.-de 500 à 600, un bond de plus 100.-de 600 à 631, un bond de plus 31.439
plus combien est égal à 631.Un plus dix plus 50 plus 100 plus 31 égal 192.Des phrases numériques sont
superposées :439 plus 1 égal 440.440 plus 10 égal 450.450 plus 50 égal 500.500 plus 100 égal 600.600 plus 31
égal 631.Tous les deuxièmes nombres sont encerclés, et additionnés pour un total de 192.
L'élève additionne pour soustraire.
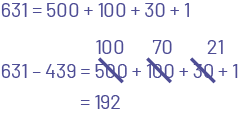
L'élève décompose le premier terme et soustrait par étapes.
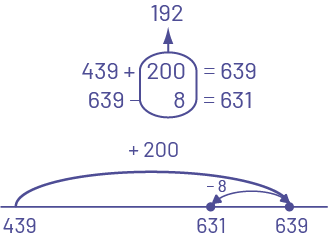 image 439 plus 200 égal 639.639 moins 8 égal
631.200 et un sont encerclés et soustraits, c’est égal à 192.Sur une droite numérique de 439 à 639, sans
intervalles réguliers, des flèches représentent les bonds suivants :De 439 à 639, bond de plus 200.De 639 à 631
bonds de moins 8.
image 439 plus 200 égal 639.639 moins 8 égal
631.200 et un sont encerclés et soustraits, c’est égal à 192.Sur une droite numérique de 439 à 639, sans
intervalles réguliers, des flèches représentent les bonds suivants :De 439 à 639, bond de plus 200.De 639 à 631
bonds de moins 8.
L'élève utlise la droite numérique et note ses déplacements.
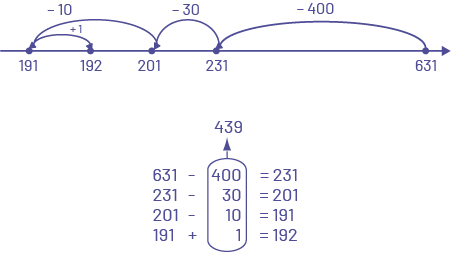 image Droite numérique de 191 à 631, sans intervalle
régulier. Des flèches représentent des bonds :-de 191 à 192, un bond de plus un.-de 631 à 231, un bond de moins
400.-de 231 à 201, un bond de moins 30.-de 201 à 191, un bond de moins dix.Des phrases numériques sont superposées
:631 moins 400 égal 231.231 moins 30 égal 201.201 moins dix égal 191.191 plus un égal 192.Tous les deuxièmes
nombres sont encerclés, et additionnés pour un total de 439.
image Droite numérique de 191 à 631, sans intervalle
régulier. Des flèches représentent des bonds :-de 191 à 192, un bond de plus un.-de 631 à 231, un bond de moins
400.-de 231 à 201, un bond de moins 30.-de 201 à 191, un bond de moins dix.Des phrases numériques sont superposées
:631 moins 400 égal 231.231 moins 30 égal 201.201 moins dix égal 191.191 plus un égal 192.Tous les deuxièmes
nombres sont encerclés, et additionnés pour un total de 439.
L'élève utilise la droite numérique et compte à rebours à partir du plus grand nombre.
Stratégies pour faciliter la compréhension des algorithmes usuels
Il est important de proposer aux élèves plusieurs activités d’exploration des algorithmes usuels en utilisant du matériel de manipulation tel que le tapis de valeur de position, les cubes emboîtables, les cadres à dix cases, le matériel de base dix, la droite numérique, etc.
Le personnel enseignant doit leur fournir plusieurs occasions de créer leurs propres algorithmes, d’expliquer leurs stratégies ainsi que les raisons qui motivent leurs choix. Il est primordial de donner aux élèves la chance et le temps d’explorer plus en profondeur les algorithmes et de favoriser les échanges. Il est important de les encourager à travailler à deux (un ou une élève prend en note les étapes de la démarche alors que l’autre travaille avec la représentation concrète). La compréhension du sens des étapes d’un algorithme usuel se développe lorsque le personnel enseignant permet aux élèves de le comparer à leur propre algorithme afin d’établir des liens entre les deux démarches comme « additionner de gauche à droite et combiner ».
Addition sur les nombres à plusieurs chiffres sans regroupement
Une addition de grands nombres peut être représentée sur une droite numérique. Par exemple, les élèves pourraient effectuer \(435\; + \;223\) en décomposant \(223 \ \left( {200\; + \;15\; + \;8} \right)\) et en représentant l’opération comme suit :
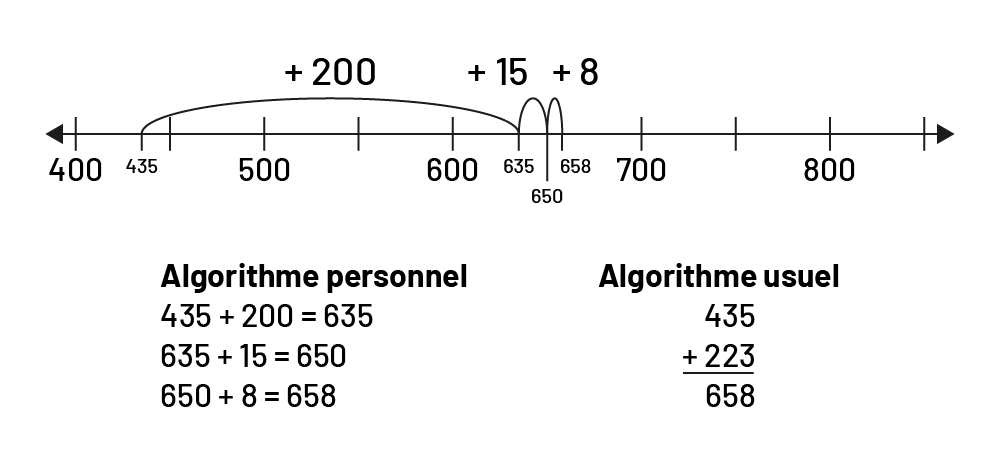 image
Droite numérique graduée de 400 à 800 par intervalles de 50.Des tirets sont indiqués aux nombres 435, 635, 650 et
658.Un bond de plus 200 est représenté entre les tirets 435 et 635.Un autre bond de plus 15 est représenté entre les
tirets 635 et 650.Un autre bond de plus 8 est représenté entre les tirets 650 et 658.Algorithme personnel435 plus 200
égal 635635 plus 15 égal 650650 plus 8 égal 658Algorithme usuelAddition verticale de 435 plus 223 égal 658.
image
Droite numérique graduée de 400 à 800 par intervalles de 50.Des tirets sont indiqués aux nombres 435, 635, 650 et
658.Un bond de plus 200 est représenté entre les tirets 435 et 635.Un autre bond de plus 15 est représenté entre les
tirets 635 et 650.Un autre bond de plus 8 est représenté entre les tirets 650 et 658.Algorithme personnel435 plus 200
égal 635635 plus 15 égal 650650 plus 8 égal 658Algorithme usuelAddition verticale de 435 plus 223 égal 658.
Au fil du temps, les élèves développent progressivement leur sens de l’abstraction et peuvent utiliser la même stratégie sans avoir recours à une droite numérique, mais en effectuant le calcul mentalement.
Addition sur les nombres à plusieurs chiffres avec regroupement
(Van de Walle et Folk, 2005, p. 191)
Il est important que les élèves puissent s’exercer à échanger des groupes de 10 unités en dizaines, des groupes de 10 dizaines en centaines, etc. Les élèves ont besoin de l’appui de représentations visuelles de regroupements afin de développer une compréhension conceptuelle de l’algorithme.
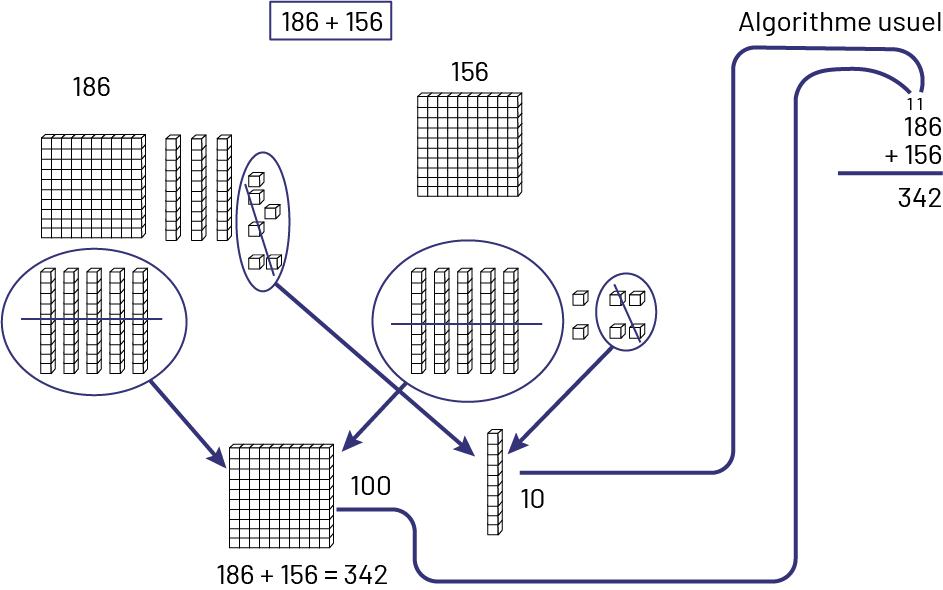
Le matériel de base dix aide certains élèves à visualiser l’opération plus clairement. Voici comment le matériel de base dix peut servir pour représenter les additions.
Exemple
 image
186 plus 56.Le nombre 186 est représenté par une planchette de 100 petits cubes accompagnée de 8 réglettes et de 6
petits cubes individuels représentent le nombre 186.Le nombre 156 est représenté par une planchette de 100 petits
cubes, 5 réglettes et 6 petits cubes individuels. Les 6 petits cubes du nombre 186 sont encerclés et barrés pour
former une réglette de dix avec 4 des 6 petits cubes du nombre 156.5 des 8 réglettes du nombre 186 sont encerclées et
barrées additionnées aux 5 réglettes du nombre 156 qui sont aussi encerclées et barrées pour former une planchette de
100.186 plus 156 égal 342.Après avoir créé ces liens, il reste dans l’image 3 planchettes, 4 réglettes et 2 petits
cubes, ce qui démontre le résultat de l’opération 186 plus 156 égal 342.Algorithme usuel:L'opération, 186 plus 156
égal 342, est démontrée de façon verticale et des flèches partant de la nouvelle planchette formée ainsi que de la
nouvelle réglette formée précédemment montrent la centaine et la dizaine qui sont ajoutées au-dessus de
l’addition.
image
186 plus 56.Le nombre 186 est représenté par une planchette de 100 petits cubes accompagnée de 8 réglettes et de 6
petits cubes individuels représentent le nombre 186.Le nombre 156 est représenté par une planchette de 100 petits
cubes, 5 réglettes et 6 petits cubes individuels. Les 6 petits cubes du nombre 186 sont encerclés et barrés pour
former une réglette de dix avec 4 des 6 petits cubes du nombre 156.5 des 8 réglettes du nombre 186 sont encerclées et
barrées additionnées aux 5 réglettes du nombre 156 qui sont aussi encerclées et barrées pour former une planchette de
100.186 plus 156 égal 342.Après avoir créé ces liens, il reste dans l’image 3 planchettes, 4 réglettes et 2 petits
cubes, ce qui démontre le résultat de l’opération 186 plus 156 égal 342.Algorithme usuel:L'opération, 186 plus 156
égal 342, est démontrée de façon verticale et des flèches partant de la nouvelle planchette formée ainsi que de la
nouvelle réglette formée précédemment montrent la centaine et la dizaine qui sont ajoutées au-dessus de
l’addition.
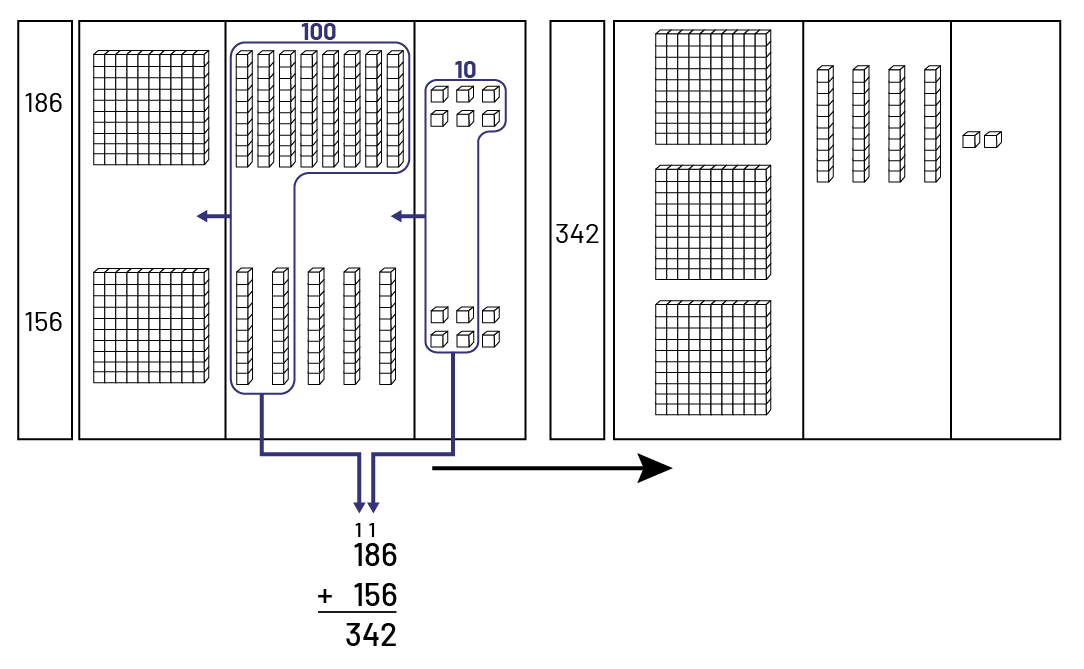
Les élèves peuvent aussi avoir recours à un tapis de valeur de position qui permet d’organiser le matériel selon la position du chiffre dans le nombre.
 image
Tapis de position de valeur.De gauche à droite, dans le tableau de l’addition, on peut y voir: - Les 2 nombres à
additionner: 186 et 156- La position des centaines: chacun des 2 nombres a une planchette de 100 petits cubes.- La
position des dizaines: le nombre 186 a 8 réglettes et le nombre 156 a 5 réglettes.- La position des unités: le nombre
186 a 6 petits cubes et le nombre 156 a aussi 6 petits cubesDans la colonne de la position des unités, on voit que les
6 cubes du nombre 186 sont mis dans un ensemble de dix avec 4 des cubes du nombre 156 et de cet ensemble formant une
réglette part une flèche montrant que cette dizaine est déplacée vers la gauche pour ajouter une dizaine.Dans la
colonne de la position des dizaines, les 8 réglettes du nombre 186 et 2 réglettes du nombre 156 sont entourées pour
former une nouvelle planchette, donc 100 unités. Une flèche part de ce nouvel ensemble et montre que cette centaine
est déplacée vers la gauche dans la position des centaines.La nouvelle dizaine et la nouvelle centaine sont ajoutées à
l’opération verticale 186 plus 156 et identifiées par des “ uns “ au-dessus des dizaines et des centaines.Une grosse
flèche part de ce tapis de valeur et va vers un deuxième tapis de valeur à droite où le résultat de l’équation, 342,
est illustré à l’aide de 3 planchettes dans la position des centaines, de 4 réglettes dans la position des dizaines et
de 2 unités.
image
Tapis de position de valeur.De gauche à droite, dans le tableau de l’addition, on peut y voir: - Les 2 nombres à
additionner: 186 et 156- La position des centaines: chacun des 2 nombres a une planchette de 100 petits cubes.- La
position des dizaines: le nombre 186 a 8 réglettes et le nombre 156 a 5 réglettes.- La position des unités: le nombre
186 a 6 petits cubes et le nombre 156 a aussi 6 petits cubesDans la colonne de la position des unités, on voit que les
6 cubes du nombre 186 sont mis dans un ensemble de dix avec 4 des cubes du nombre 156 et de cet ensemble formant une
réglette part une flèche montrant que cette dizaine est déplacée vers la gauche pour ajouter une dizaine.Dans la
colonne de la position des dizaines, les 8 réglettes du nombre 186 et 2 réglettes du nombre 156 sont entourées pour
former une nouvelle planchette, donc 100 unités. Une flèche part de ce nouvel ensemble et montre que cette centaine
est déplacée vers la gauche dans la position des centaines.La nouvelle dizaine et la nouvelle centaine sont ajoutées à
l’opération verticale 186 plus 156 et identifiées par des “ uns “ au-dessus des dizaines et des centaines.Une grosse
flèche part de ce tapis de valeur et va vers un deuxième tapis de valeur à droite où le résultat de l’équation, 342,
est illustré à l’aide de 3 planchettes dans la position des centaines, de 4 réglettes dans la position des dizaines et
de 2 unités.
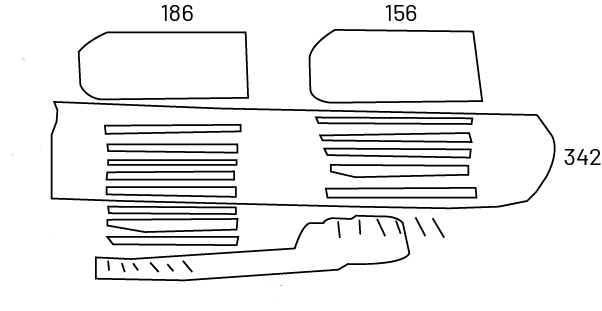
La même expression numérique \(\left( {186\; + \;156} \right)\) peut être représentée à l’aide d’illustrations. Ainsi, les élèves démontrent un certain niveau d’abstraction puisqu’un dessin quelconque représente 100, 10 ou 1.
 image
Une illustration qui représente les nombres 186 et 156, pour un total de 342 éléments.186 : un bloc qui représente la
centaine, 8 bâtons représentent les dizaines et 6 bâtonnets représentent les unités.156 : un bloc représente la
centaine, 5 bâtons représentent les dizaines et 6 bâtonnets représentent les unités.Un ensemble regroupe dix bâtons de
dizaine.Un autre ensemble regroupe, 5 bâtonnets.
image
Une illustration qui représente les nombres 186 et 156, pour un total de 342 éléments.186 : un bloc qui représente la
centaine, 8 bâtons représentent les dizaines et 6 bâtonnets représentent les unités.156 : un bloc représente la
centaine, 5 bâtons représentent les dizaines et 6 bâtonnets représentent les unités.Un ensemble regroupe dix bâtons de
dizaine.Un autre ensemble regroupe, 5 bâtonnets.
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 122-124.
Soustraction sans échange
Comme pour l’addition, les élèves utilisent souvent du matériel de manipulation pour effectuer des soustractions. Cette stratégie les aide à saisir le concept de retrait, même si elle n’est pas très efficace lorsqu’il s’agit de grands nombres.

Le matériel de base dix permet aux élèves d’effectuer la soustraction au moyen d’un retrait.
Exemple
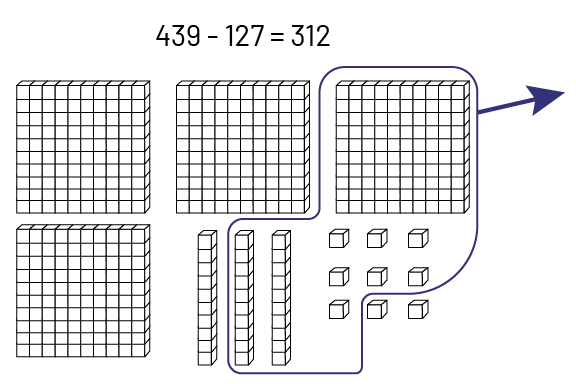
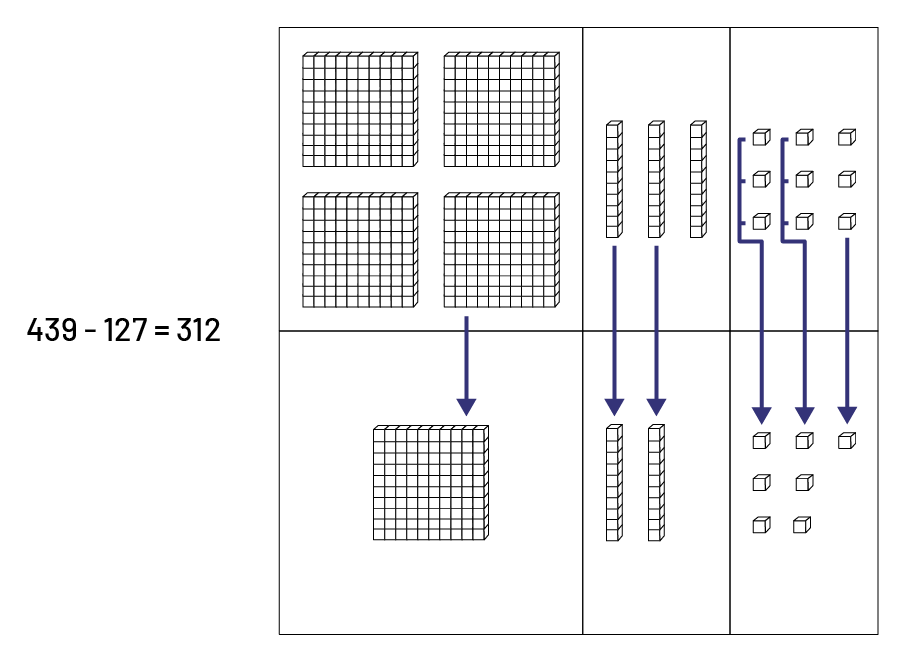
Si les élèves utilisent le tapis de valeur de position pour la soustraction, certains élèves sont portés à représenter les deux termes. La soustraction est alors effectuée par comparaison.
Exemple
 image
Tapis de valeur de position.439 moins 127 égal 312.Un tableau comprenant 3 colonnes représentant de gauche à droite
les centaines, les dizaines et les unités ainsi que 2 lignes.La ligne du haut représente le nombre 439 avec 4
planchettes, 3 réglettes ainsi que 9 unités.Une flèche part de l’une des planchettes et pointe vers la ligne
au-dessous pour montrer qu’une planchette est soustraite.Une flèche partant de 2 réglettes et pointant vers la ligne
au-dessous pour montrer que 2 dizaines sont soustraites.7 petits cubes indiqués avec des tirets et ayant une flèche
partant de cette direction et allant vers la ligne au-dessous montrant que 7 unités sont soustraites.La ligne du bas
dans le tapis représente le nombre qui est soustrait, 127, avec une planchette de 100 unités, 2 réglettes de dix
unités et 7 unités.
image
Tapis de valeur de position.439 moins 127 égal 312.Un tableau comprenant 3 colonnes représentant de gauche à droite
les centaines, les dizaines et les unités ainsi que 2 lignes.La ligne du haut représente le nombre 439 avec 4
planchettes, 3 réglettes ainsi que 9 unités.Une flèche part de l’une des planchettes et pointe vers la ligne
au-dessous pour montrer qu’une planchette est soustraite.Une flèche partant de 2 réglettes et pointant vers la ligne
au-dessous pour montrer que 2 dizaines sont soustraites.7 petits cubes indiqués avec des tirets et ayant une flèche
partant de cette direction et allant vers la ligne au-dessous montrant que 7 unités sont soustraites.La ligne du bas
dans le tapis représente le nombre qui est soustrait, 127, avec une planchette de 100 unités, 2 réglettes de dix
unités et 7 unités.
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6eannée, p. 127-128.
Soustraction avec échange
(Van de Walle et Folk, 2005, p. 193)
L’exploration de la soustraction avec échange en favorise la compréhension conceptuelle. Le personnel enseignant devrait encourager les élèves à utiliser le tapis de valeur de position et du matériel de base dix pour modéliser la soustraction avec échange. Les élèves peuvent travailler à deux. Elles et ils peuvent passer à la forme écrite de l’algorithme une fois qu’elles et ils en ont développé une solide compréhension par l’entremise de modèles.
Dans le cas du problème \(325\; - \;118\), les élèves représentent le 1er nombre (325) avec du matériel de base 10 sur la portion supérieure du tapis de valeur de position. Ne pouvant pas retirer 8 unités puisqu’il n’y en a que 5, les élèves échangent une dizaine pour 10 unités.
image Tapis de valeur de position.3 colonnes de gauche à droite intitulées centaines, dizaines et unités.Il y a 3 planchettes de 100 unités dans la colonne des centaines. Il y a 2 réglettes de dix unités dans la colonne des dizaines et 5 unités dans la colonne des unités.À droite on voit l’opération verticale 325 moins 118.On ne peut retirer 8 unités puisqu’il n’y en a que 5.
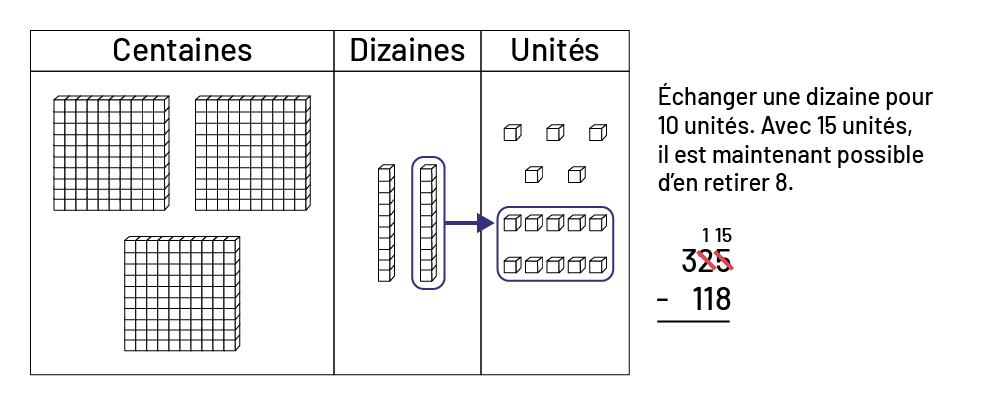 image Tapis de valeur de position.3 colonnes de gauche à droite
intitulées centaines, dizaines et unités.Il y a 3 planchettes de 100 unités dans la colonne des centaines. Il y a 2
réglettes de dix unités dans la colonne des dizaines et 5 unités dans la colonne des unités.Dans la colonne des
dizaines, une des 2 réglettes est encerclée. Une flèche part de cette direction et va dans la colonne des unités où on
peut voir dix unités additionnelles encerclées aussi.Échanger une dizaine pour dix unités. Avec 15 unités, il est
maintenant possible d’en retirer 8.L’opération 325 moins 118 est inscrite à la verticale et on voit que les 25 du 325
est barré et sur le dessus du 5 on peut voir le nombre 15 puisqu’une dizaine d’unités a été ajoutée et au-dessus du 2
il y a un “ un ” car une dizaine a été retirée.
image Tapis de valeur de position.3 colonnes de gauche à droite
intitulées centaines, dizaines et unités.Il y a 3 planchettes de 100 unités dans la colonne des centaines. Il y a 2
réglettes de dix unités dans la colonne des dizaines et 5 unités dans la colonne des unités.Dans la colonne des
dizaines, une des 2 réglettes est encerclée. Une flèche part de cette direction et va dans la colonne des unités où on
peut voir dix unités additionnelles encerclées aussi.Échanger une dizaine pour dix unités. Avec 15 unités, il est
maintenant possible d’en retirer 8.L’opération 325 moins 118 est inscrite à la verticale et on voit que les 25 du 325
est barré et sur le dessus du 5 on peut voir le nombre 15 puisqu’une dizaine d’unités a été ajoutée et au-dessus du 2
il y a un “ un ” car une dizaine a été retirée.
Elles et ils obtiennent ainsi un groupe de 15 unités à partir duquel il leur est maintenant possible d’en retirer 8 de sorte qu’il en reste 7. Il faut encourager les élèves à regrouper les unités sur le tapis afin de mieux organiser leur travail.
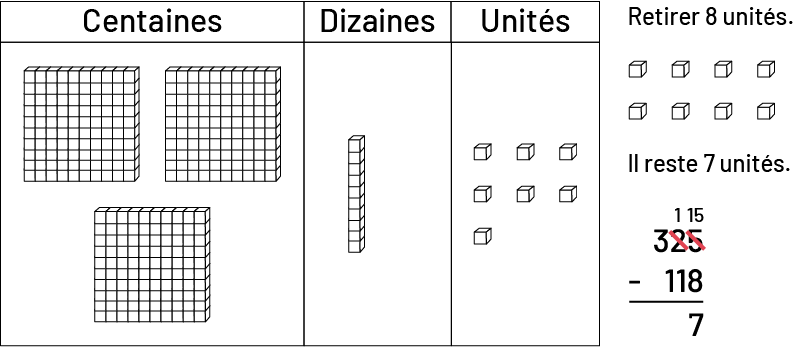 image
Tapis de valeur de position.3 colonnes de gauche à droite intitulées centaines, dizaines et unités.Il y a 3
planchettes dans la colonne des centaines, une réglette dans la colonne des dizaines et 7 unités dans la colonne des
unités.À droite du tapis de valeur:Retirer 8 unités.8 petits cubes individuels sont illustrés.Il reste 7
unités.L’opération verticale 325 moins 118 égal 7 est inscrite et le 2 de 325 est barré et remplacé par un. Le 5 de
325 est barré et remplacé par 15.
image
Tapis de valeur de position.3 colonnes de gauche à droite intitulées centaines, dizaines et unités.Il y a 3
planchettes dans la colonne des centaines, une réglette dans la colonne des dizaines et 7 unités dans la colonne des
unités.À droite du tapis de valeur:Retirer 8 unités.8 petits cubes individuels sont illustrés.Il reste 7
unités.L’opération verticale 325 moins 118 égal 7 est inscrite et le 2 de 325 est barré et remplacé par un. Le 5 de
325 est barré et remplacé par 15.
Les élèves retirent maintenant 1 dizaine et 1 centaine et les placent à l’extérieur du tapis.

Donc, \(325\; - \;118\; = \;207\)
Source : Guide d'enseignement efficace des mathématiques de la maternelle à la 6e année, p. 58-59.
Les élèves peuvent aussi utiliser la droite numérique pour effectuer une soustraction. Par exemple, pour calculer \(263\; - \;45\), elles et ils peuvent utiliser la compensation afin de travailler avec des nombres plus familiers. Puisque \(263\; + \;2\; = \;265\), on peut donc effectuer \(265\; - \;45\; = \;220\) et ensuite, soustraire 2 pour compenser \((263\; + \;2\; - \;45\; - \;2)\).
Les élèves n’ont pas à transcrire leur réflexion sous forme d’expression numérique, mais peuvent néanmoins utiliser la droite numérique pour illustrer leur démarche :
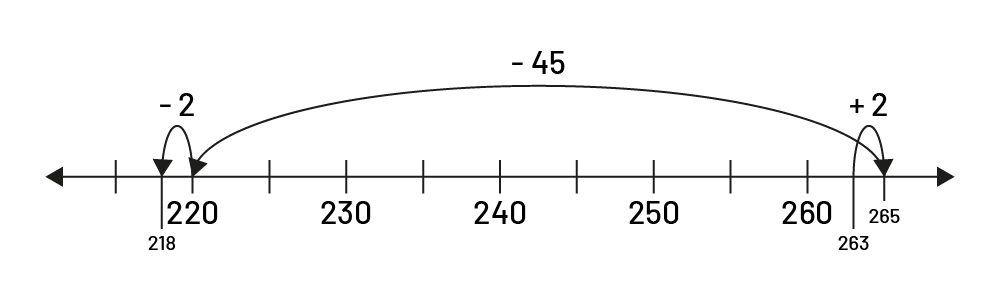 image
Droite numérique graduée de 220 à 260 par intervalles de 5.Il y a un tiret à 263. Une flèche partant d’un tiret
indiqué à 263 et allant au tiret 265 marquant un bond de plus 2 est indiquée. Une autre flèche partant de 265 et
pointant le tiret 220 marque un bon de moins 45.Une flèche partant du tiret 220 et pointant un tiret à 218 marque un
bond de moins 2.
image
Droite numérique graduée de 220 à 260 par intervalles de 5.Il y a un tiret à 263. Une flèche partant d’un tiret
indiqué à 263 et allant au tiret 265 marquant un bond de plus 2 est indiquée. Une autre flèche partant de 265 et
pointant le tiret 220 marque un bon de moins 45.Une flèche partant du tiret 220 et pointant un tiret à 218 marque un
bond de moins 2.
La droite numérique peut également être employée avec la décomposition selon les valeurs de position des chiffres du nombre \((263\; - \;40\; = \;223,\;223\; - \;5\; = \;218)\) :
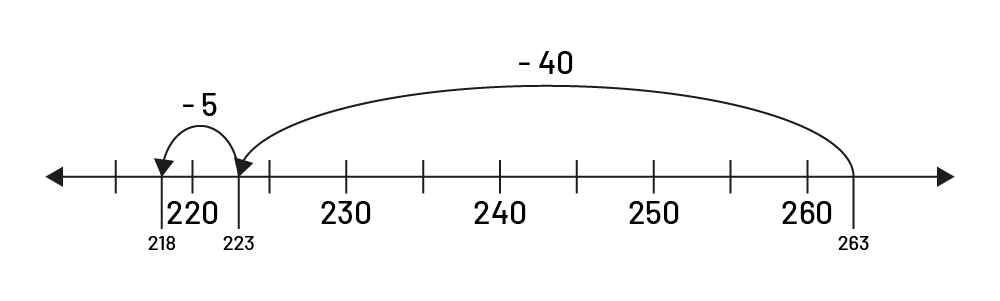
La droite numérique ouverte permet aux élèves de procèder par bonds significatifs \((263\; - \;3\; = \;260,\;260\; - \;40\; = \;220,\;220\; - \;2\; = \;218)\) :
 Droite numérique graduée montrant l’intervalle entre 220 et 260. Un tiret indique 263. Une flèche part
de cette direction et pointe le tiret 260 montrant un bond de moins 3. Une flèche parant de 260 et pointant vers 220
montre un bond de moins 40. Une flèche partant du tiret 220 et pointant le tiret 218 montre un bon de moins 2.
Droite numérique graduée montrant l’intervalle entre 220 et 260. Un tiret indique 263. Une flèche part
de cette direction et pointe le tiret 260 montrant un bond de moins 3. Une flèche parant de 260 et pointant vers 220
montre un bond de moins 40. Une flèche partant du tiret 220 et pointant le tiret 218 montre un bon de moins 2.
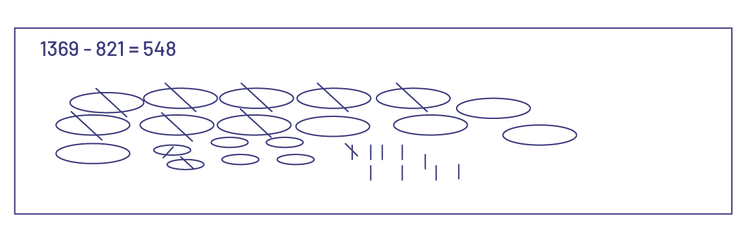
Les élèves peuvent utiliser des dessins pour illustrer rapidement une expression numérique comme \(1\;369\; - \,821\). Les nombres peuvent être représentés par des lignes, des cercles, des points, etc. Un retrait peut être exprimé par des barres sur le dessin. Pour \(1\;369\; - \,821\), il faut enlever 8 centaines, 2 dizaines et 1 unité des 13 centaines, 6 dizaines et 9 unités.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 127-129.
Habileté : représenter et résoudre des problèmes relatifs à l’addition et à la soustraction de nombres décimaux jusqu’aux dixièmes
L’élève utilisera ses connaissances antérieures relatives aux nombres naturels pour résoudre des problèmes comprenant des nombres décimaux et utilisera les mêmes types d’algorithmes personnels, puisqu’ils sont basés sur le sens du nombre plutôt que sur la position des chiffres. Par conséquent, l’élève pourra expliquer clairement le sens des calculs effectués.
Source : UPBALF Numération et sens du nombre/Mesure 6e, module 3, série 2, p. 179
Exemple
Sophie fabrique deux colliers de perles.
Elle utilise 1,5 m de fil pour faire le premier et 2,7 m de fil pour faire le second. Quelle longueur de fil a-t-elle utilisée en tout?
Pour additionner efficacement des nombres décimaux, les élèves doivent comprendre la valeur de position des chiffres qui composent chacun des nombres et en tenir compte dans leurs calculs. Les élèves doivent aussi reconnaître que la virgule est un repère qui permet d’identifier la valeur de position des chiffres. Lors d’une addition, pour assurer la correspondance des valeurs de position, on peut aligner les virgules. Pour les élèves qui ont un bon sens de l’addition et de la valeur de position, l’alignement de la virgule n’est pas une règle à mémoriser, mais une façon de tenir compte des valeurs de position.
Lorsqu’on additionne des nombres décimaux, le concept de regroupement est utilisé tout comme lors de l’addition de nombres naturels. Par exemple, on peut ajouter 7 dixièmes à 5 dixièmes pour former 12 dixièmes. Or, puisque le système décimal ne permet pas d’inscrire deux chiffres dans une même position, les élèves doivent comprendre le concept de regroupement.
5 dixièmes + 7 dixièmes = 12 dixièmes
(La languette  représente l’unité.)
représente l’unité.)

Le système décimal ne permet pas d’inscrire deux chiffres dans une même position.

Puisque 10 dixièmes peuvent être regroupés en 1 unité, on a une unité et 2 dixièmes.

La quantité « 12 dixièmes » s’écrit 1,2.
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 98-99.
Le matériel de base dix et le tapis de valeur de position sont une aide précieuse. Avec ce matériel, les quantités de même valeur sont réunies de façon explicite, par exemple, les dixièmes sont additionnés avec les dixièmes. Lorsque les élèves travaillent avec du matériel de base dix, elles et ils utilisent leurs connaissances de la valeur de position et, de ce fait, approfondissent le concept de regroupement, en transférant ce concept appliqué aux nombres naturels à des situations impliquant des nombres décimaux. Les élèves reconnaissent alors que peu importe la valeur de position, chaque fois que 10 éléments se retrouvent dans une position, ils sont remplacés par 1 groupe de 10 qui est placé dans la position à sa gauche. L’utilisation de ce type de matériel accroît la compréhension des élèves et leur fait découvrir des algorithmes pour l’addition de nombres décimaux.
Il est important que le personnel enseignant amène les élèves à établir des liens entre ces stratégies afin de consolider l’addition de nombres décimaux. Voici différentes stratégies pour résoudre le problème ci-dessous :
\(1,5\; + \;2,7\)
Afin d’estimer la somme, il est possible de raisonner comme suit : \(1,5\; + \;2,7\), c’est à peu près \(2\; + \;3\), donc environ 5.
Addition à l’aide de matériel de base dix
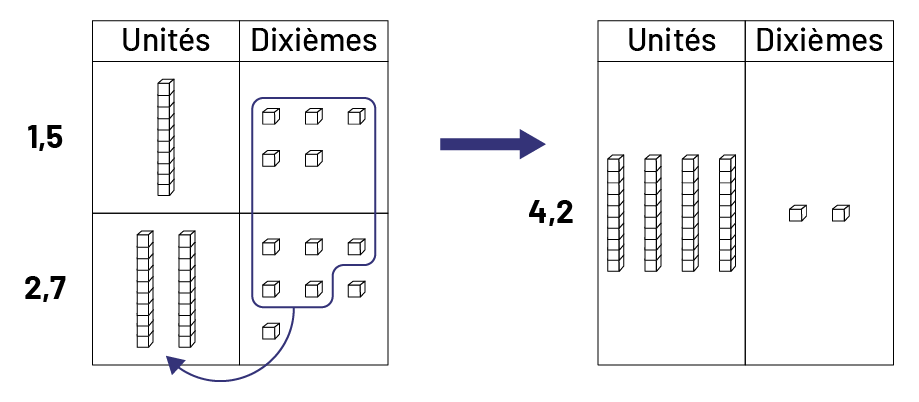
Pour additionner les deux quantités, on représente chacun des deux nombres à l’aide de matériel de base dix sur un tapis de valeur de position. En réunissant le matériel, on obtient 3 unités et 12 dixièmes. On regroupe 10 dixièmes qu’on échange contre 1 unité. On a alors 4 unités et 2 dixièmes, soit 4,2.
 image
Tapis de valeur de position.De gauche à droite il y a 2 colonnes:Unités et dixièmes.La première ligne illustre le
nombre un, virgule 5. Il y a une languette de dix unités dans la colonne des unités et 5 cubes dans la colonne des
dixièmes.La deuxième ligne illustre le nombre 2, virgule 7.Il y a 2 languettes dans la colonne des unités et 7 cubes
dans la colonne des dixièmes.Les 5 cubes de la première ligne et 5 cubes de la deuxième ligne sont encerclés. Une
flèche part de cet ensemble et pointe vers les unités.Une flèche part de ce tapis de valeur et montre un deuxième
tapis de valeur illustrant le nombre 4 virgule 2.Il y a 4 languettes dans la colonne des unités et 2 cubes dans la
colonne des dixièmes.
image
Tapis de valeur de position.De gauche à droite il y a 2 colonnes:Unités et dixièmes.La première ligne illustre le
nombre un, virgule 5. Il y a une languette de dix unités dans la colonne des unités et 5 cubes dans la colonne des
dixièmes.La deuxième ligne illustre le nombre 2, virgule 7.Il y a 2 languettes dans la colonne des unités et 7 cubes
dans la colonne des dixièmes.Les 5 cubes de la première ligne et 5 cubes de la deuxième ligne sont encerclés. Une
flèche part de cet ensemble et pointe vers les unités.Une flèche part de ce tapis de valeur et montre un deuxième
tapis de valeur illustrant le nombre 4 virgule 2.Il y a 4 languettes dans la colonne des unités et 2 cubes dans la
colonne des dixièmes.
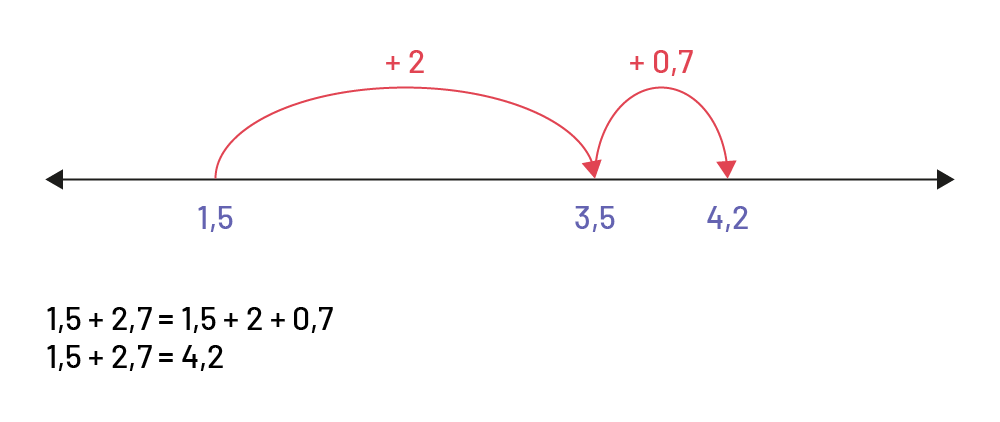
Addition à l’aide d’une droite numérique
\(\begin{array}{l}1,5 + 2,7 = 1,5 + 2 + 0,7\\1,5 + 2,7 = 4,2\;\;\,\end{array}\)
 image
Droite numérique non graduée où sont inscrit les nombres en ordre croissant: “ un, virgule 5”, “ 3 virgule 5 ” et “ 4,
virgule 2 ”.Une flèche part de, un, virgule 5 et pointe 3, virgule 5 montrant un bond de plus 2. Une autre flèche part
de 3, virgule 5 et pointe 4, virgule 2 montrant un bond de plus zéro, virgule 7.Un, virgule 5 plus 2, virgule 7 égal
un, 5 plus 2 plus zéro, 7.Un, virgule 5 plus 2, virgule 7 égal 4, virgule 2.
image
Droite numérique non graduée où sont inscrit les nombres en ordre croissant: “ un, virgule 5”, “ 3 virgule 5 ” et “ 4,
virgule 2 ”.Une flèche part de, un, virgule 5 et pointe 3, virgule 5 montrant un bond de plus 2. Une autre flèche part
de 3, virgule 5 et pointe 4, virgule 2 montrant un bond de plus zéro, virgule 7.Un, virgule 5 plus 2, virgule 7 égal
un, 5 plus 2 plus zéro, 7.Un, virgule 5 plus 2, virgule 7 égal 4, virgule 2.
Addition à l’aide de mots
\(\begin{array}{l}1{\rm{\ et \ 5 \ dixièmes}}\;{\rm{ + }}\;{\rm{2 \ et \ 7 \ dixièmes}}\\{\rm{ = }}\;{\rm{3 \ et \ 12 \ dixièmes}}\\{\rm{ = }}\;{\rm{3}}\;{\rm{ + }}\;{\rm{1 \ et \ 2 \ dixièmes}}\\{\rm{ = }}\;4{\rm{ \ et \ 2 \ dixièmes}}\\{\rm{ = }}\;{\rm{4}}{\rm{,2}}\end{array}\)
Addition à l’aide d’un algorithme personnel
Les nombres sont décomposés selon les valeurs de position.
\(\begin{array}{l}1,5 + 2,7\\0,5 + 0,7 = 1,2\\1 + 2 = 3\\3 + 1,2 = 4,2\end{array}\)
Raisonnement d’un élève
- 5 dixièmes plus 7 dixièmes, ça donne 12 dixièmes, ce qui est équivalent à 1 unité et 2 dixièmes (1,2).
- 1 unité plus 2 unités, ça donne 3 unités.
- Alors \(1,5\; + \;2,7\; = \;4,2\).
Addition à l’aide de l’algorithme usuel
\(\begin{array}{l}\;\,{}^11,5\\\underline { + 2,7} \\\;\;\,4,2\end{array}\)
Raisonnement d’un élève
- 5 dixièmes plus 7 dixièmes, ça donne 12 dixièmes. J’échange 10 dixièmes contre 1 unité. J’ai donc 1 unité et 2 dixièmes. J’écris un 2 en bas dans la colonne des dixièmes et un petit 1 en haut dans la colonne des unités.
- 1 unité plus 1 unité plus 2 unités, ça donne 4 unités. J’écris un 4 en bas dans la colonne des unités.
- En tout, il y a 4 unités et 2 dixièmes.
Exemple de comparaison
Christophe utilise 3,4 m de fil pour fabriquer deux colliers de perles.
Sophie utilise 1,2 m de fil pour fabriquer deux bracelets de perles.
Combien de fil Christophe utilise-t-il de plus que Sophie?
Au cours de la soustraction, il est important, comme ce l’était pour l’addition, de tenir compte de la valeur de position des chiffres qui composent les nombres. Les stratégies pour soustraire les nombres décimaux sont essentiellement les mêmes que celles utilisées pour soustraire les nombres naturels.
Soustraction à l’aide de matériel de base dix
Lorsqu’elles et ils utilisent du matériel concret pour représenter une soustraction, les élèves peuvent réellement manipuler les quantités. Pour déterminer une différence, les élèves peuvent comparer une quantité à une autre ou retirer une quantité d’une autre. En outre, les élèves découvrent, en utilisant ce matériel, qu’il est parfois nécessaire d’effectuer des échanges pour pouvoir déterminer plus facilement la différence entre les quantités.
\(3,4\; - \;1,2\; = \;?\)
On représente chaque nombre à l’aide de matériel de base dix et on apparie les quantités semblables (en rouge) dans chaque position. La différence est représentée par les quantités qui restent dans le nombre 3,4 (en bleu). Ainsi, on obtient \(3,4\; - \;1,2\; = \;2,2\).
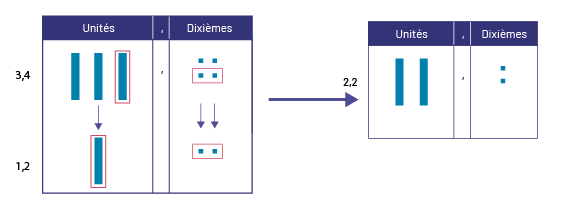 image Tapis
de valeur de position.3 colonnes de gauche à droite:Unités, virgule et dixièmes.Le nombre 3, virgule 4 est représenté
au haut du tapis avec 3 bâtonnets dans la colonne des unités et 4 cubes dans la colonne des dixièmes.Le nombre un,
virgule 2 est représenté au bas par un bâtonnet dans la colonne des unités et 2 cubes dans la colonne des
dixièmes.L’un des bâtonnets du nombre 3, virgule 4 est encerclé en rouge et une flèche partant de cette direction
pointe le bâtonnet du nombre un, virgule 2. 2 des cubes du nombre 3, virgule 4 sont encerclés en rouge et une flèche
partant de cette direction pointe les 2 cubes du nombre un, virgule 2.Une flèche part de ce tapis de valeur et pointe
un autre tapis de valeur à droite.Le nombre 2, virgule 2 est illustrée dans ce tableau par 2 bâtonnets dans la colonne
des unités et 2 cubes dans la colonne des dixièmes.
image Tapis
de valeur de position.3 colonnes de gauche à droite:Unités, virgule et dixièmes.Le nombre 3, virgule 4 est représenté
au haut du tapis avec 3 bâtonnets dans la colonne des unités et 4 cubes dans la colonne des dixièmes.Le nombre un,
virgule 2 est représenté au bas par un bâtonnet dans la colonne des unités et 2 cubes dans la colonne des
dixièmes.L’un des bâtonnets du nombre 3, virgule 4 est encerclé en rouge et une flèche partant de cette direction
pointe le bâtonnet du nombre un, virgule 2. 2 des cubes du nombre 3, virgule 4 sont encerclés en rouge et une flèche
partant de cette direction pointe les 2 cubes du nombre un, virgule 2.Une flèche part de ce tapis de valeur et pointe
un autre tapis de valeur à droite.Le nombre 2, virgule 2 est illustrée dans ce tableau par 2 bâtonnets dans la colonne
des unités et 2 cubes dans la colonne des dixièmes.
Christophe utilise 2,2 m de plus que Sophie.
Exemple de retrait
Christophe utilise 3,4 m de fil pour fabriquer deux colliers de perles. Il utilise 1,2 m de fil pour faire le premier collier. Quelle sera la longueur de fil utilisé pour faire le second collier?
\(3,4\; - \;1,2\; = \;?\)
Soustraction à l’aide de matériel de base dix
On représente le nombre 3,4 à l’aide de matériel de base dix. Ensuite, on retire l’équivalent du nombre 1,2. Il reste alors sur le tapis la différence entre les deux nombres, soit 2,2.
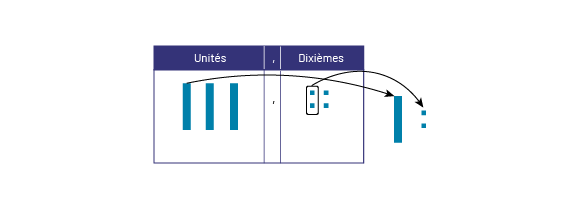 image Tapis
de valeur de position.3 colonnes de gauche à droite:Unités, virgule et dixièmes.Le nombre 3, virgule 4 est représenté
au haut du tapis avec 3 bâtonnets dans la colonne des unités et 4 cubes dans la colonne des dixièmes.Une flèche
partant de l’un des bâtonnets du tapis et sort à l’extérieur du tapis pour pointer un bâtonnet.Une flèche partant de 2
cubes encerclés à l'intérieur du tapis de valeur et pointe à l’extérieur du tapis vers 2 petits cubes.
image Tapis
de valeur de position.3 colonnes de gauche à droite:Unités, virgule et dixièmes.Le nombre 3, virgule 4 est représenté
au haut du tapis avec 3 bâtonnets dans la colonne des unités et 4 cubes dans la colonne des dixièmes.Une flèche
partant de l’un des bâtonnets du tapis et sort à l’extérieur du tapis pour pointer un bâtonnet.Une flèche partant de 2
cubes encerclés à l'intérieur du tapis de valeur et pointe à l’extérieur du tapis vers 2 petits cubes.
Le fil utilisé pour le second collier mesure 2,2 m.
Exemple d’échange
Ahmed veut fabriquer des colliers aussi. Il avait 2,4 m de fil. Il utilise 1,6 m pour le premier collier. Quelle sera la longueur de fil utilisé pour faire le second collier?
\[2,4 - 1,6 = ?\]
Soustraction à l’aide de matériel de base dix
On représente le nombre 2,4 à l’aide de matériel de base dix. En voulant utiliser la stratégie de retrait pour effectuer la soustraction, on se rend compte qu’il n’y a que 4 dixièmes sur le tapis alors qu’on doit retirer 6 dixièmes. Dans ce cas, on échange 1 unité contre 10 dixièmes. On retire ensuite l’équivalent du nombre 1,6.
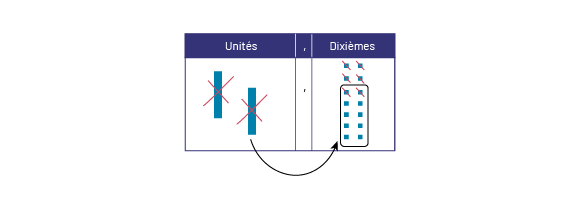 image Tapis
de valeur de position.3 colonnes de gauche à droite:Unités, virgule et dixièmes.Il y a 2 bâtonnets dans la colonne des
unités et 4 cubes dans la colonne des dixièmes. Les 2 bâtonnets sont barrés et une flèche partant de cette direction
pointe la colonne des dixièmes un ensemble de dix unités encerclées. Dans la colonne des dixièmes, les 4 cubes
individuels sont barrés et 2 des dix cubes encerclés sont barrés.
image Tapis
de valeur de position.3 colonnes de gauche à droite:Unités, virgule et dixièmes.Il y a 2 bâtonnets dans la colonne des
unités et 4 cubes dans la colonne des dixièmes. Les 2 bâtonnets sont barrés et une flèche partant de cette direction
pointe la colonne des dixièmes un ensemble de dix unités encerclées. Dans la colonne des dixièmes, les 4 cubes
individuels sont barrés et 2 des dix cubes encerclés sont barrés.
Il reste alors sur le tapis, la différence entre les deux nombres, soit 0,8.
Donc, la longueur de fil utilisé pour faire le second collier est 0,8 m.
Soustraction à l’aide d’une droite numérique
 image
Droite numérique non graduée.On peut y voir de gauche à droite les nombres zéro, virgule 8, un, un, virgule 4 et 2,
virgule 4 inscrits.2, virgule 4 moins un égal un, virgule 4.Une flèche part du nombre 2, virgule 4 et pointe vers un,
virgule 4 montrant un bond de moins un.Un, virgule 4 moins zéro, virgule 4 égal un.Une flèche partant d’un, virgule 4
et pointant vers un montre un bond de moins zéro, virgule 4.Un, moins zéro virgule 2 égal zéro, virgule 8.Une flèche
partant de, un et pointant vers zéro, virgule 8 montrant un bond de moins zéro, virgule 2.
image
Droite numérique non graduée.On peut y voir de gauche à droite les nombres zéro, virgule 8, un, un, virgule 4 et 2,
virgule 4 inscrits.2, virgule 4 moins un égal un, virgule 4.Une flèche part du nombre 2, virgule 4 et pointe vers un,
virgule 4 montrant un bond de moins un.Un, virgule 4 moins zéro, virgule 4 égal un.Une flèche partant d’un, virgule 4
et pointant vers un montre un bond de moins zéro, virgule 4.Un, moins zéro virgule 2 égal zéro, virgule 8.Une flèche
partant de, un et pointant vers zéro, virgule 8 montrant un bond de moins zéro, virgule 2.
Soustraction à l’aide d’un algorithme personnel
\(\begin{align}2,&4\; - \;1,6\\2,&4\; - \;\left( {1,4\; + \;0,2} \right)\\2,&4\; - \;1,4 = \;1\\ &1\; - \;0,2 = \;0,8\end{align}\)
Raisonnement d’un élève
J’ai décomposé le 2e nombre et j’ai enlevé les quantités selon les valeurs de position.
Donc, la longueur de fil utilisé pour faire le second collier est 0,8 m.
Soustraction à l’aide de l’algorithme usuel
L’algorithme usuel permet aussi d’effectuer une soustraction avec des nombres décimaux. Cependant, il faut s’assurer de faire correspondre les valeurs de position.
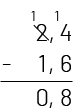
Raisonnement d’un élève
- Il est impossible de retirer 6 dixièmes de 4 dixièmes, alors j’échange 1 unité contre 10 dixièmes. Il me reste alors 1 unité et j’ai maintenant 14 dixièmes. 14 dixièmes moins 6 dixièmes, c’est 8 dixièmes.
- 1 unité moins 1 unité, c’est 0 unité.
Donc, la longueur de fil utilisé pour faire le second collier est 0,8 m.
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 99-104.
Il faut prêter une attention particulière aux soustractions portant sur des nombres comportant un 0 à la position des unités ou des dizaines. Van de Walle et Folk (2005, p. 193) suggèrent qu’il est plus efficace d’aborder cette problématique lorsque les élèves travaillent avec le matériel de manipulation. Il importe de donner aux élèves l’occasion de discuter des différentes stratégies utilisées pour effectuer des soustractions avec de tels nombres.
Source : Guide d'enseignement efficace des mathématiques de la maternelle à la 6e année, p. 59.
Connaissance : algorithme
Les algorithmes sont des ensembles de règles et d’actions ordonnées nécessaires à la résolution d’une addition, d’une soustraction, d’une multiplication ou d’une division. En termes simples, un algorithme est la « recette » d’une opération. (Kilpatrick, Swafford et Findell, 2001, p. 103)
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 75.
Connaissance : algorithme personnel
Stratégie, généralement développée par l’élève, pour effectuer une opération.
Exemple
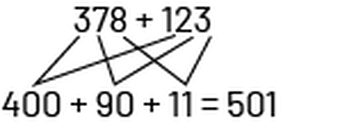 image
378 plus 123.Un peu plus bas l’équation 400 plus 90 plus 11 égal 501 est écrite.Entre les 2 opérations, on voit des
lignes relier les centaines des nombres 378 et 123 au nombre 400.D’autres lignes relient les dizaines des nombres 378
et 123 au nombre 90.D’autres lignes relient les unités des nombres 378 et 123 au nombre 11.
image
378 plus 123.Un peu plus bas l’équation 400 plus 90 plus 11 égal 501 est écrite.Entre les 2 opérations, on voit des
lignes relier les centaines des nombres 378 et 123 au nombre 400.D’autres lignes relient les dizaines des nombres 378
et 123 au nombre 90.D’autres lignes relient les unités des nombres 378 et 123 au nombre 11.
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 76.
