B2.6 Représenter et résoudre des problèmes relatifs à la division d’un nombre naturel à deux ou à trois chiffres par un nombre naturel à un chiffre, en exprimant le reste sous forme de fraction, si nécessaire, à l’aide d’outils appropriés, y compris de dispositions rectangulaires.
Habileté : résoudre des problèmes de division d’un nombre naturel à deux ou trois chiffres par un nombre naturel à un chiffre
Les élèves acquièrent une bonne compréhension de la multiplication et de la division ainsi que des relations entre les nombres en résolvant des problèmes écrits. Les types de problèmes présentés ci-après à l’aide d’exemples peuvent aider les élèves à percevoir les faits numériques de base relatifs à la multiplication et à la division de diverses façons, selon qu’il s’agit de problèmes de groupes égaux, de comparaison ou de combinaisons. Le recours aux problèmes pour présenter les faits numériques de base oblige les élèves à raisonner pour trouver des solutions et permet ainsi de développer un meilleur sens des opérations.
Groupes égaux : nombre de groupes inconnu (groupement)
L’école a acheté 150 livres pour les classes et prépare des bacs. Un parent bénévole met 30 livres dans chaque bac. Combien de bacs le parent a-t-il utilisés?
\[150 \div 30 = ?\;\;{\rm{ou}}\;\;?\; \times 30 = 150\]
La disposition rectangulaire
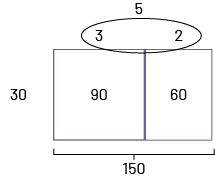image
Disposition rectangulaire de 2 colonnes.À gauche du rectangle le chiffre 30.Au-dessus de la première colonne du
rectangle est indiqué 3. Au-dessus de la deuxième colonne du rectangle est indiqué 2.À l’intérieur du rectangle dans
la première colonne se trouve le résultat de la multiplication de ce qui est écrit à gauche par ce qui est écrit en
haut, soit 90.Dans la deuxième colonne du rectangle, il est indiqué 60, soit le résultat de la multiplication de ce
qui est écrit à gauche par ce qui est écrit au-dessus.Les chiffres 3 et 2 sont encerclés et un 5 est indiqué au-dessus
du cercle.Un crochet représente la largeur totale du rectangle et indique 150.
Le parent bénévole a utilisé 5 bacs pour les livres.
Groupes égaux : taille des groupes inconnue (partage)
L’école achète 150 livres pour chacune des 5 classes. Un parent bénévole prépare 5 bacs de livres. Combien de livres contient chaque bac?
image Un rectangle jaune intitulé 150 livres.Sous le rectangle
jaune, 5 petits rectangles de même dimension et totalisant la même largeur que le rectangle jaune. Chacun est indiqué
par un point d’interrogation.Un crochet regroupe les 5 petits rectangles rouges et indique: “ 5 bacs ”.
\[150 \div 5 = ?\;\;{\rm{ou}}\;\;5\; \times ? = 150\]
Un partage
\[10 + 10 + 10 = 30\]
Chaque bac contient 30 livres.
Problème de combinaison
Combinaison : taille d’un ensemble inconnue
Mustapha a des chemises et des pantalons neufs. Il a 15 tenues différentes en tout. S’il a trois pantalons, combien de chemises Mustapha a-t-il?
\[15 \div 3 = ?\;\;{\rm{ou}}\;\;\;3\; \times ? = 15\]
Partage égal – diagramme en arbre
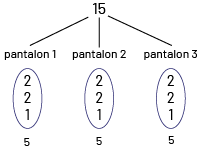
\[15 \div 3 = 5\;\;{\rm{ou}}\;\;3\; \times 5 = 15\]
Mustapha a 5 chemises.
Source : Guide d'enseignement efficace des mathématiques de la maternelle à la 6e année, p. 10-11.
La notion du reste
Dans une division, le concept de reste survient lorsque le quotient n’est pas un nombre entier. Par exemple, \(10\; \div \;3\; = \;3\) reste \(1\) ou \(3 \frac{1}{3}\) . Pour plusieurs élèves, le reste n’est qu’un nombre qui paraît dans la « recette » de la division (par exemple, \(123\; \div \;5\; = \;24\;\) reste \(3\)).
Cependant, lorsque l’opération surgit d’un contexte, le reste doit être traité afin de pouvoir répondre adéquatement au problème. Ainsi, les élèves peuvent développer l’habileté à traiter le reste si elles et ils sont en situation de résolution de problèmes.
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 86.
Il est recommandé d’exposer les élèves à des divisions avec un reste dès le jeune âge, puisque dans la vie de tous les jours, les divisions que nous faisons ne sont pas toujours des chiffres ronds. Il est important de présenter ces divisions dans un contexte relié au vécu des élèves, car c’est une notion abstraite.
Exemple
- Sans contexte
\(10\; \div \;3\; = \;3\;\;{\rm{R1}}\)
Que représente R1, un enfant ou un bonbon?
- Avec contexte
Dans l’exemple ci-après, le reste est réparti équitablement et exprimé sous la forme d’une fraction.
Lucas veut donner 10 muffins à ses 3 amis. Il souhaite que chaque ami reçoive le même nombre de muffins. Combien de muffins donne-t-il à chacun de ses 3 amis?
En contexte, il est plus facile de déterminer ce que représente le R1. Ici, c’est un muffin.
Chaque enfant aura \(3\; + \;\frac{1}{3}\) muffins ou \(3\frac{1}{3}\).
Le reste est exprimé en fraction, puisqu’un muffin peut être divisé.
Source : L'@telier – Ressources pédagogiques en ligne (atelier.on.ca),
Stratégies de calculs
Voici une panoplie de stratégies qui peuvent être utilisées pour effectuer la division. Elles répondent à des besoins variés et facilitent l’apprentissage des élèves.
Pour faciliter la lecture et la compréhension de cette section, les opérations sont présentées sous forme d’expressions numériques et de modèles. En classe, le personnel enseignant devrait aussi représenter les opérations horizontalement, par exemple : \(432 \div 5\).
Devant une division à effectuer, soit que l’on cherche le nombre de groupes – sens de groupement – soit que l’on cherche la taille de chaque groupe – sens de partage. Ainsi, les stratégies de calcul peuvent différer selon le sens de la division. Les élèves doivent avoir l’occasion d’apprendre et d’utiliser plusieurs stratégies pour résoudre des problèmes de division des deux types.
Comme pour les autres opérations, au départ les élèves peuvent utiliser du matériel de manipulation.
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 121, 140-145.
Exemple 1
Mme Langlois a 125 gommettes. Tous les jours, elle donne 5 gommettes à des élèves. Au bout de combien de jours Mme Langlois aura-t-elle donné toutes ses gommettes?
\[125 \div 5 = ?\]
Estimation
\(\begin{align}125 \div 5 &\approx 100 \div 5 \\ &\approx 20\end{align}\)
Stratégie 1
Division à l’aide de la disposition rectangulaire
Je décompose 125 en \(100\; + \;25\), qui sont 2 multiples de 5. Ceci facilite la division.
Je divise premièrement 100 par 5 et ensuite 25 par 5. J’additionne les deux quotients pour obtenir le nombre de jours pour que Mme Langlois donne toutes ses gommettes.
image Papier quadrillé de 5 rangées de 25 petits carrés.5 est inscrit
à gauche du papier.20 est inscrit au-dessus du papier vis-à-vis des 20 premiers carrés et 5 est inscrit au-dessus du
papier au-dessus des 5 dernières rangées.Le nombre 100 est indiqué au centre des 20 premières colonnes.Le nombre 25
est indiqué au centre des 5 dernières colonnes.
\(20\; + \;5\; = \;25\)
Elles et ils pourront alors conclure que Mme Langlois sera en mesure de donner des gommettes pendant 25 jours.
Stratégie 2
Division à l’aide de la droite numérique double
Je décompose 125 en \(100\; + \;25\), qui sont 2 multiples de 5. Ceci facilite la division.
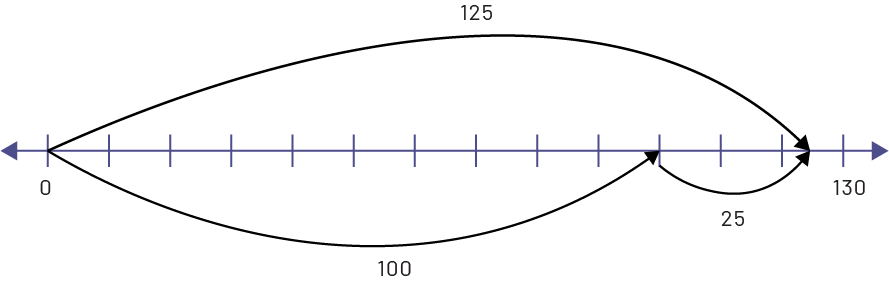image
Droite numérique de zéro à 130 par intervalles de dix.Une flèche part de zéro et pointe 100, montrant un bond de plus
100.Une autre flèche part de 100 et pointe 125, montrant un bond de 25.Une flèche part de zéro et pointe 125 montrant
un bond de 125.
\(\begin{align}100 \div 5 &= 20\\25 \div 5 &= 5\\20 + 5 &= 25\end{align}\)
Elles et ils pourront alors conclure que Mme Langlois sera en mesure de donner des gommettes pendant 25 jours.
Exemple 2
À l’école Aureste, la directrice achète 252 paquets de feuilles quadrillées. Elle les partage également entre 8 groupes-classes. Combien de paquets chaque groupe-classe reçoit-il?
\[252 \div 8 = ?\]
Estimation
\(\begin{align}252 \div 8 &\approx 240 \div 8\\ &\approx 30\end{align}\)
Je sais que ma réponse est environ 30 paquets.
Stratégie 1
Division à l’aide de la disposition rectangulaire
Je décompose 252 en multiples de 8 que je connais, soit \(80\; + \;80\; + \;80\) et il me reste 12.
Je sais que \(80\; \div \;8\; = \;10\). Il reste 12. Je peux donc faire un autre groupe de 8. Il me reste 4 paquets. Je peux diviser chaque paquet en 2 pour former 8 demi-paquets.
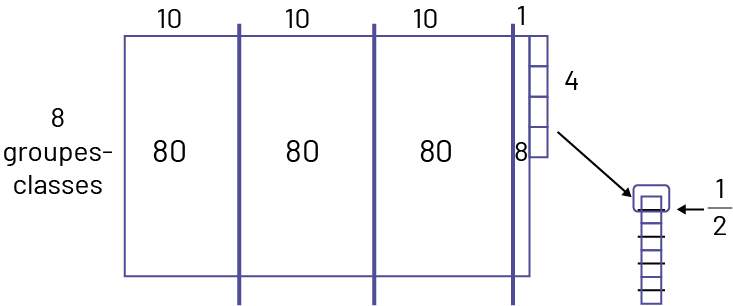image
Disposition rectangulaire.À gauche du rectangle:8 groupes classes.Au-dessus du rectangle:-Première colonne:
dix-deuxième colonne: dix-troisième colonne: dix-quatrième colonne: un-cinquième colonne: 4 unitésÀ l’intérieur du
rectangle, de gauche à droite:-80-80-80-8Une flèche part des 4 unités à part et pointe une colonne de 8 demi-unités.La
fraction un de 2 est inscrite à côté de cette colonne de 8 demi-unités.
\(\ 10 + 10 + 10 + 1 + \frac{1}{2} = 31\frac{1}{2}\)
Elle distribue \(\ 31\frac{1}{2}\) paquets à chaque groupe-classe.
Source : adapté de Les mathématiques... un peu, beaucoup, à la folie!, Guide pédagogique, Numération et sens du nombre/Mesure, 4e année, Module 2, Série 2, Introduction, p. 172.
Stratégie 2
Division à l’aide de la multiplication
Je décompose 252 en multiples de 8 que je connais, soit 80 + 80 + 80 et il me reste 12.
Je multiplie \(8 \times 10\), 3 fois. J’additionne les produits. Je soustrais 240 de 252, ce qui me donne 12. Je multiple 8 x 1, je peux donc distribuer 31 paquets par classe et il me reste 4 paquets.
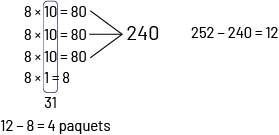image
4 multiplications inscrites une au-dessous de l’autre.8 fois dix égal 80.8 fois dix égal 80.8 fois dix égal 80.8 fois
un égal 8Les 3 dix et le un sont encerclés et le nombre 31 est inscrit pour cet ensemble.Les 3 nombres 80 sont reliés
par 3 lignes au nombre 240.12 moins 8 égal 4 paquets.252 moins 240 égal 12.
Il reste 4 paquets. Je peux diviser chaque paquet en 2 pour avoir 8 demi-paquets.
Elle distribue alors \(31\frac{1}{2}\) paquets à chaque groupe-classe.
Source : adapté de Les mathématiques... un peu, beaucoup, à la folie!, Guide pédagogique, Numération et sens du nombre/Mesure, 4e année, Module 2, Série 2, Introduction, p. 172.
Connaissance : types de division
Il existe deux types de problèmes de division. Les autres découlent de la multiplication.
Le type « groupement »
Ici, on connaît le nombre total d’objets et le nombre d’objets dans chaque groupe. On cherche le nombre de groupes.
Le type « partage »
Ici, on partage un ensemble d’objets également entre un certain nombre de groupes ou de personnes. On connaît le nombre total d’objets et le nombre de groupes. On cherche le nombre d’objets dans chaque groupe.