B2.7 Démontrer la relation entre l’addition répétée d’une fraction unitaire et la multiplication de cette fraction unitaire par un nombre naturel, à l’aide d’outils, de schémas et de la notation fractionnaire usuelle.
Habileté : démontrer la relation entre l’addition répétée d’une fraction unitaire et la multiplication de cette fraction unitaire par un nombre naturel, à l’aide d’outils, de schémas et de la notation fractionnaire usuelle
Les activités qui requièrent de compter les parties d’un tout, une à une, et de les mettre en relation avec le tout développent la compréhension du rôle du numérateur et du dénominateur. De plus, les élèves apprennent que le nom donné à chaque partie est déterminé par le nombre de parties retrouvées dans le tout. Ainsi, lorsqu’un tout est divisé en deux parties équivalentes, il s’agit de demis; lorsqu’il est divisé en trois parties équivalentes, il s’agit de tiers; lorsqu’il est divisé en quatre parties équivalentes, il s’agit de quarts. À partir de cinq parties équivalentes, on ajoute le suffixe ième au nombre de parties pour obtenir des cinquièmes, des vingtièmes, etc. L’élève qui maîtrise le concept de partie d’un tout n’a pas besoin de recréer l’image de la « tarte » pour comprendre, par exemple, que six sixièmes (\(\frac{6}{6}\)) forment un tout. Ainsi, afin d’identifier la fraction représentée ci-dessous, son raisonnement pourrait être le suivant : « Je compte les morceaux (1, 2, 3, 4, 5 et 6) et j’en conclus qu’il s’agit de sixièmes. Puisque cinq (5) parties sont ombrées, je peux affirmer que cinq sixièmes (\(\frac{5}{6}\)) de la figure est ombrée. »
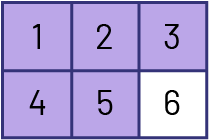
Ce processus les amène aussi à reconnaître qu’une fraction peut correspondre à la somme de fractions unitaires.
Exemple
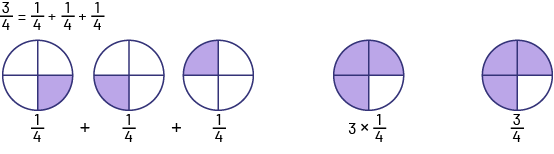 image 3 de
4 est égal à un de 4 plus un de 4 plus un de 4.Un cercle est divisé en 4 quarts dont celui en bas à droite est mauve.
Un de 4.À droite du premier cercle on voit le symbole plus.Un deuxième cercle divisé en 4 quarts dont le quart en bas
à gauche est mauve. Un de 4.À droite du deuxième cercle on voit le symbole plus.Un troisième cercle divisé en 4 quarts
dont le quart en haut à gauche est mauve. Un de 4.À droite de ces 3 premiers cercles, il y a un autre cercle divisé en
4 quarts dont les quarts du haut et celui du bas à gauche sont mauves. 3 multiplié par un de 4.Il y a un dernier
cercle divisé en 4 quarts dont les quarts du haut et celui du bas à gauche sont mauves. 3 de 4.
image 3 de
4 est égal à un de 4 plus un de 4 plus un de 4.Un cercle est divisé en 4 quarts dont celui en bas à droite est mauve.
Un de 4.À droite du premier cercle on voit le symbole plus.Un deuxième cercle divisé en 4 quarts dont le quart en bas
à gauche est mauve. Un de 4.À droite du deuxième cercle on voit le symbole plus.Un troisième cercle divisé en 4 quarts
dont le quart en haut à gauche est mauve. Un de 4.À droite de ces 3 premiers cercles, il y a un autre cercle divisé en
4 quarts dont les quarts du haut et celui du bas à gauche sont mauves. 3 multiplié par un de 4.Il y a un dernier
cercle divisé en 4 quarts dont les quarts du haut et celui du bas à gauche sont mauves. 3 de 4.
Les élèves qui ont compté, par exemple, des parties équivalentes de touts peuvent expliquer que le dénominateur représente ce qui est compté (par exemple, des sixièmes) et que le numérateur représente combien il y en a. Van de Walle et Folk (2005, p. 229) soulèvent un point intéressant, à savoir que les termes numérateur et dénominateur sont des mots plutôt savants qui relèvent davantage du monde des adultes qui comprennent le lien entre numération et numérateur et le lien entre dénomination et dénominateur. Il suggère que la connaissance de ces termes, chez les élèves du cycle moyen, ne témoigne nullement de cette compréhension.
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 34-35
Les fractions sont utilisées dans diverses tâches quotidiennes telles qu’en cuisine pour mesurer les ingrédients. Or, les opérations sur les fractions sont trop souvent perçues comme une série de règles qu’il faut apprendre et maîtriser. Cette perception a pour effet de promouvoir l’obéissance à des règles plutôt qu’une réelle compréhension des opérations. Ainsi, les élèves qui en sont à leurs premières armes avec les opérations sur les fractions risquent d’apprendre une liste de procédures dont le sens leur échappe et, par le fait même, de les oublier ou de les appliquer de façon erronée. Cet ensemble de règles et de procédures vient souvent embrouiller le sens de l’opération, comme le démontre cette interrogation d’un élève : « Puis-je additionner les fractions comme je le fais avec les nombres naturels? »
Apprentissage des opérations fondamentales
L’acquisition d’habiletés en calcul doit reposer sur l’acquisition d’un sens des opérations, sinon ces habiletés restent à un niveau superficiel et mécanique. Van de Walle et Folk (2005, p. 244 et 245) suggèrent des lignes directrices pour guider l’enseignement des opérations sur les fractions.
Présenter des tâches simples en contexte
Les principes qui guident le développement de stratégies personnelles de résolution de problèmes s’appliquent autant aux fractions qu’aux nombres naturels. Plusieurs études – notamment celles de Huinker (1998, p. 170-182) et Lappan et Bouck (1998, p. 183-197) – valorisent les approches informelles mises de l’avant par les élèves pour résoudre des problèmes. Cette phase exploratoire, riche en apprentissages, sert d’assise à l’acquisition de méthodes plus conventionnelles. D’ailleurs, dans ses écrits, Huinker (1998) souligne l’importance du contexte et de la résolution de problèmes pour le développement des algorithmes personnels. Il précise cependant qu’un problème n’a pas besoin d’être très élaboré ni même difficile. Il doit plutôt avoir pour objectif d’approfondir simultanément, chez les élèves, le sens de la fraction et le sens de l’opération. Par exemple, il peut s’agir d’un problème pour lequel les élèves ne savent pas d’avance comment s’y prendre. Elles et ils le résolvent et ensuite elles et ils analysent leur démarche, ce qui les amène à reconnaître l’opération effectuée et à représenter la situation de façon symbolique.
Faire le lien entre les opérations sur les nombres naturels et celles sur les fractions
Les élèves ont déjà acquis une compréhension solide de l’addition et de la soustraction et elles et ils ont certaines notions de la multiplication et de la division. Il est important de faire des liens entre les opérations sur les nombres naturels et celles sur les fractions. Par exemple, l’addition de 3 huitièmes et de 2 huitièmes est la même que celle de 3 bonbons et de 2 bonbons. Seule la notation est différente et plus complexe. De même, les élèves qui possèdent des représentations justes de la multiplication (par exemple, \(4\; \times \;5\) peut être lu « 4 fois 5 » et être représenté par \(5\; + \;5\; + \;5\; + \;5\)) comprendront la multiplication d’une fraction par un nombre naturel (par exemple, \(\ 4 \times \frac{1}{8}\) peut être lu « 4 fois \(\frac{1}{8}\)» et être représenté par \(\frac{1}{8} + \frac{1}{8} + \frac{1}{8} + \frac{1}{8}\)). Le concept sous-jacent est donc le même et il importe de faire le lien entre les deux situations.
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 74-75.
Multiplication
Au cycle moyen, les élèves ont déjà un bagage de connaissances sur la multiplication. En effet, depuis le primaire, elles et ils explorent des concepts reliés à la multiplication à l’aide de matériel concret, de la calculatrice, d’illustrations et de symboles. En 4e année, la multiplication de fractions est limitée. Ce type de multiplication peut être compris en le reliant à l’addition répétée. Ainsi, les élèves saisissent facilement que \(\ 3 \times \frac{1}{2}\), qu’on peut lire « 3 fois un demi », est une multiplication qui peut être représentée par l’addition répétée, soit \(\frac{1}{2} + \frac{1}{2} + \frac{1}{2}\). Cependant, il est plus difficile de donner un sens à la multiplication d’un nombre naturel par une fraction (par exemple, \(\frac{1}{2} \times 3\)). Il existe un lien entre le concept de multiplication par une fraction et celui de fraction d’un ensemble.
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 78.
Dans le cas de la multiplication d’une fraction par un nombre naturel, il est important de mettre l’accent sur le sens de la multiplication qui peut être associé à l’addition répétée. Prenons, par exemple, la situation suivante :
« De combien de cartons l’élève qui doit distribuer un demi-carton à quatre camarades aura-t-il besoin? »
La vidéo suivante montre la relation entre la multiplication d’un nombre naturel par une fraction unitaire et l’addition répétée de cette fraction unitaire.
 Description de la vidéo
Description de la vidéo
Description à venir
Connaissance : fraction unitaire
Fraction dont le numérateur est un (1).
Exemples
\(\frac{1}{3}\) \(\frac{1}{9}\)
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 35.
Connaissance : notation fractionnaire
Nous appelons la fraction écrite \(\frac{a}{b}\) la notation fractionnaire. La notation fractionnaire \(\frac{a}{b}\) est généralement associée au concept de partie d’un tout. Le tout peut être un élément ou un ensemble d’éléments.
Exemple
- J’ai donné un quart (\(\frac{1}{4}\)) de mon sandwich à Alex.
- Un quart (\(\frac{1}{4}\)) de mes billes sont bleues.

Or, la notation fractionnaire peut être aussi associée à d’autres concepts tels que la division, le rapport et l’opérateur.
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 36.
Connaissance : numérateur
Nombre de parties équivalentes du tout dont se compose la fraction.
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 34.
