B1.3 Représenter des fractions équivalentes à partir des demis jusqu’aux douzièmes, y compris des fractions impropres et des nombres fractionnaires, à l’aide d’outils appropriés, dans divers contextes.
Activité 1 : trouver des fractions équivalentes à l’aide de divers modèles
Voici des représentations qui permettent à l’élève de développer un sens de ce que sont des fractions équivalentes.
Modèle de longueur
Le modèle de longueur est très utile pour représenter des fractions, trouver des fractions équivalentes et effectuer des opérations avec des fractions. Il s’avère un référentiel visuel très efficace qui permet aux élèves de mieux comprendre la quantité représentée par une fraction.
Activité interactive : L'@telier - Ressources pédagogiques en ligne (atelier.on.ca).
On peut représenter la même chose avec des languettes de papier quadrillé métrique (le tout a 36 carrés de long). La longueur des touts doit être la même.
Source : L'@telier - Ressources pédagogiques en ligne (atelier.on.ca).
Modèle de surface
Penser à la manière dont les élèves doivent résoudre ce problème.
La partie rouge représente la partie de la crêpe française que Mona a mangée.
Si cette crêpe avait été coupée en 4, en 6 ou en 8 parties égales, est-ce que Mona aurait pu en manger la même quantité?
Activité interactive : Cliquer ensuite sur « Solution » afin de voir une suggestion de stratégie de résolution de problème.
Source : L’@telier — Ressources pédagogiques en ligne (atelier.on.ca).
Modèle d’ensemble
Réfléchir à la manière dont les élèves doivent résoudre ce type de problème en utilisant des jetons.
Janika affirme que les 3 douzièmes des mois de l’année commencent par la lettre « j ». Elle montre ses affirmations à l’aide de jetons. Elle utilise des jetons verts pour représenter les mois qui commencent par un « j » et des jetons rouges pour représenter les mois qui commencent par une autre lettre. Après avoir regardé la représentation, elle dit même que \(\frac{1}{4}\) des mois commencent par un « j ». Elle place les jetons en groupes de 3 pour illustrer les 4 groupes, dont 1 représente les 3 mois qui commencent par la lettre « j ».
Activité interactive : Cliquer ensuite sur le bouton Solution afin de voir une suggestion de résolution.
Source : L’@telier — Ressources pédagogiques en ligne (atelier.on.ca).
Relation de proportionnalité
Une relation de proportionnalité est présente dans toute situation de fractions équivalentes.
Activité interactive : L’@telier — Ressources pédagogiques en ligne (atelier.on.ca).
Note : \(\frac{3}{7}\; = \;\frac{{21}}{{49}}\) sont 2 fractions équivalentes. Cette notation est aussi appelée une proportion.
Source : L’@telier — Ressources pédagogiques en ligne (atelier.on.ca).
Activité 2 : fractions équivalentes
Démarche
Remettre la feuille de travail aux élèves.
À droite du 1er rectangle, demander aux élèves d’écrire la fraction qui représente la partie ombragée.
Demander aux élèves de colorier la même surface sur les autres rectangles.
À droite des autres rectangles, demander aux élèves d’écrire la fraction qui représente les parties coloriées de chaque rectangle.
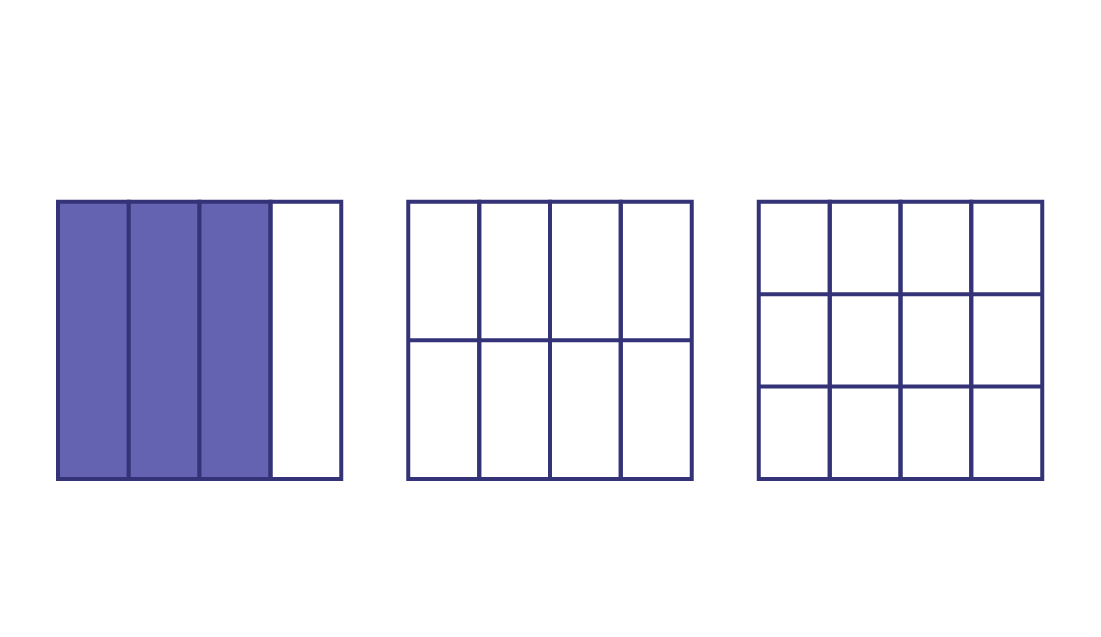
Sur le tableau, écrire les égalités suivantes :
Demander aux élèves d’expliquer le lien entre les numérateurs et les dénominateurs.
Noter le lien à l’aide de flèches et des opérations.
Demander aux élèves la règle qui permet de trouver des fractions équivalentes.
Demander aux élèves de montrer, à l’aide de matériel de manipulation, la règle qu’elles et ils ont trouvée.
image
Un carré divisé en 8 parties égales sur 2 rangées et 4 colonnes. 6 parties sont en rouge.3 sur 4 égal 6 sur 8.Le 3
multiplié par 2 égal 6.Le 4 multiplié par 2 égal 8.Un carré divisé en 12 parties égales, sur 3 rangées et 4 colonnes.
9 parties sont en rouge.3 sur 4 égal 9 sur 12.3 multiplié par 3 égal 9.4 multiplié par 3 égal 12.
Source : L’@telier — Ressources pédagogiques en ligne (atelier.on.ca)
Activité 3 : les nombres fractionnaires et les fractions impropres
Grouper les élèves par 2 ou 3 et leur remettre des mosaïques géométriques. Présenter les mosaïques en identifiant l’hexagone comme étant le tout. Amener les élèves à reconnaître que le trapèze rouge équivaut à \(\frac{1}{2}\) de l’hexagone, le losange bleu à \(\frac{1}{3}\) de l’hexagone et le triangle vert à \(\frac{1}{6}\) de l’hexagone.
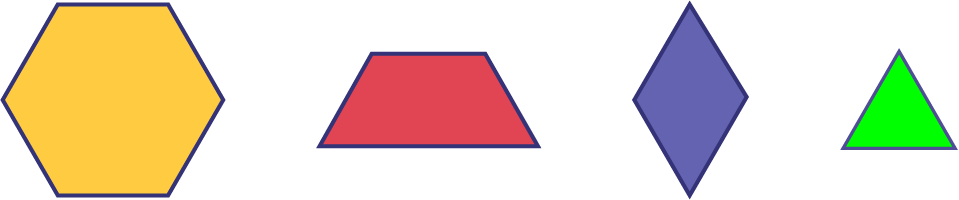
Dans un premier temps, demander aux élèves de représenter \(\frac{{16}}{3}\) d’hexagones à l’aide de mosaïques géométriques. Puisque la fraction impropre est en tiers et que le losange représente \(\frac{1}{3}\) du tout, les élèves devraient choisir 16 losanges.
Inviter les élèves à regrouper les losanges pour former des touts. Ainsi, les élèves peuvent déterminer le nombre fractionnaire correspondant à la fraction impropre donnée.
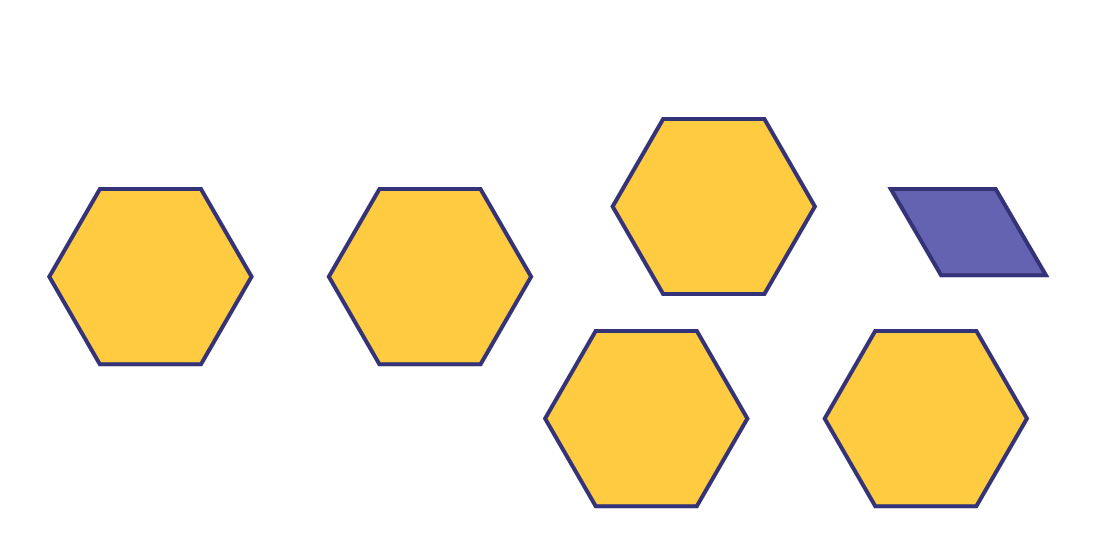
Conclure en soulignant que la fraction impropre donnée (\(\frac{{16}}{3}\)) et le nombre fractionnaire déterminé (\(5\frac{1}{3}\)) représentent une même quantité.
En suivant la même démarche, explorer d’autres équivalences (par exemple, \(\frac{{13}}{2}\; = \;6\frac{1}{2},\;\frac{{27}}{6}\; = \;4\frac{3}{6}\)) avec les élèves. Après quelques exemples, leur demander d’examiner attentivement le raisonnement utilisé afin de déterminer une stratégie qui ne nécessite pas de matériel concret.
Dans un deuxième temps, demander aux élèves de représenter \(3\frac{5}{6}\) hexagones à l’aide de mosaïques géométriques. Afin de représenter le nombre fractionnaire donné, les élèves devraient choisir 3 hexagones et 5 triangles.
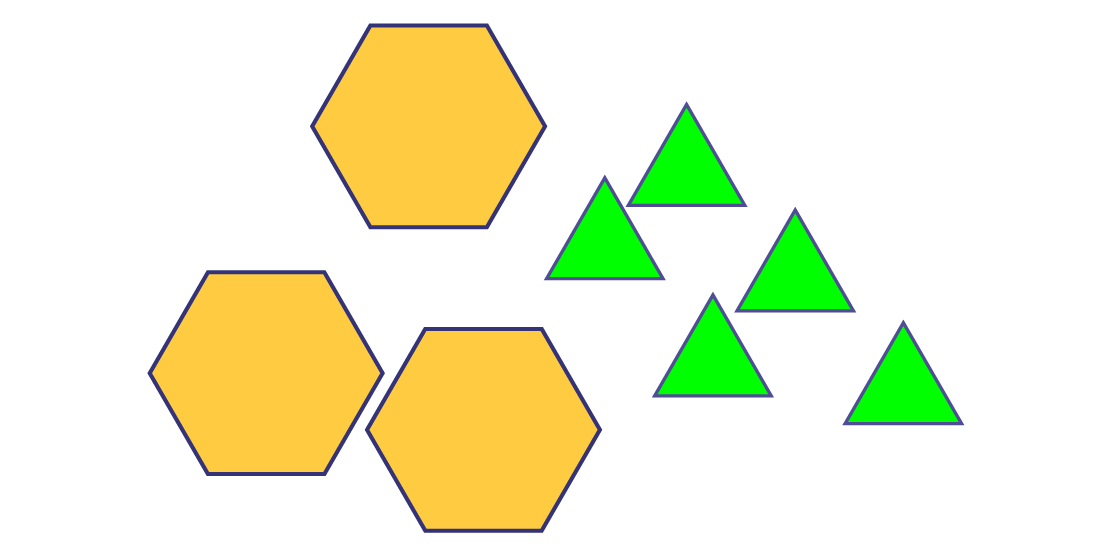
Ensuite, inviter les élèves à fractionner les touts. Ainsi, les élèves peuvent alors déterminer la fraction impropre correspondant au nombre fractionnaire donné.
Conclure en soulignant que le nombre fractionnaire donné (\(3\frac{5}{6}\)) et la fraction impropre déterminée (\(\frac{{23}}{6}\)) représentent une même quantité. En suivant la même démarche, explorer d’autres équivalences (par exemple, \(7\frac{1}{2} = \frac{15}{2};\;\;\;3\frac{2}{3}\; = \;\frac{{11}}{3}\)) avec les élèves. Après quelques exemples, leur demander d’examiner attentivement le raisonnement utilisé afin de déterminer une stratégie qui ne nécessite pas de matériel concret.
Note : Cette activité peut être réalisée avec d’autres types de matériel de manipulation (par exemple, réglettes Cuisenaire, cubes de couleur). De plus, pour approfondir la compréhension de la relation entre une fraction et son tout, le tout peut être modifié; par exemple, si le tout correspond à 2 hexagones, le triangle vert équivaut alors à \(\frac{1}{{12}}\) du tout, le losange bleu à \(\frac{1}{6}\) du tout et le trapèze rouge à \(\frac{1}{4}\) du tout.
Source: Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 157 à 159.
Activité 4 : les drapeaux
Proposer aux élèves de créer un drapeau de classe sur lequel figureront 4 éléments d’égale importance; ainsi, il sera séparé en 4 sections équivalentes.
Distribuer aux élèves une feuille présentant des rectangles congruents. Leur demander d’abord de fractionner les rectangles en quarts de diverses façons.
Ensuite, inviter des élèves à en reproduire 1 au tableau. Discuter des divers fractionnements possibles. Généralement, le tout est fractionné en 2 parties et chacune de ces parties est par la suite fractionnée en 2. Chaque partie est donc 1 demi-partie de 1 demi-partie, ce qui représente le quart du tout.
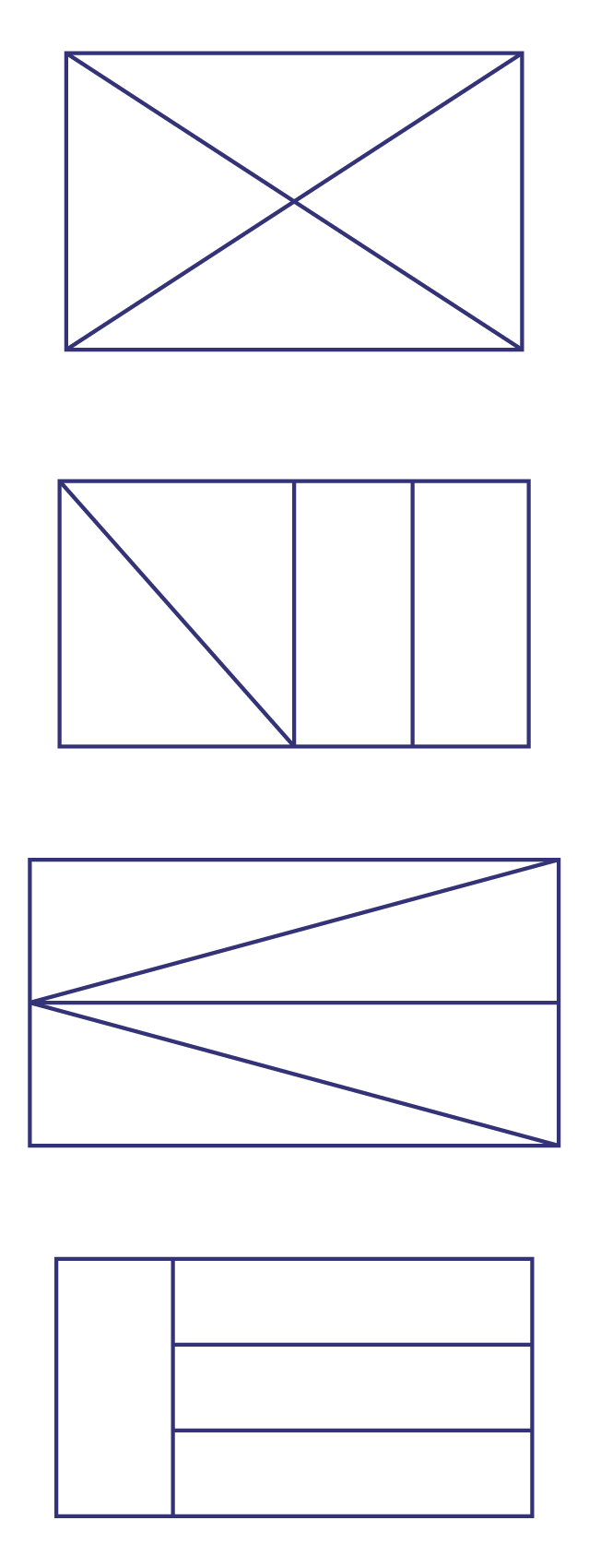
Faire remarquer aux élèves que, bien que la forme des parties diffère, chaque partie couvre la même surface, soit 1 quart du rectangle; elles sont donc toutes équivalentes.
image
Un rectangle divisé en 4 triangles, non égaux, mais équivalents.Un rectangle divisé en 2 triangles et 2 bandes
rectangulaires, elles ne sont pas égales, mais les 4 parties sont équivalentes.Un rectangle divisé en 4 triangles sur
sa longueur, les triangles ne sont pas égaux, mais ils sont équivalents.Un rectangle divisé en 4 rectangles inégaux,
mais équivalents.
Inviter les élèves à choisir un fractionnement et à créer un drapeau en respectant le critère de 4 éléments d’importance égale.
Source: Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 135.