B2.9 Représenter et créer des rapports et des taux équivalents, à l’aide d’une variété d’outils et de modèles, dans divers contextes.
Activité 1 : maquette à l’échelle
Cette activité intègre des concepts en Nombres, en Sciences et technologie ainsi qu’en Éducation artistique.
Le personnel enseignant explique qu’un fabricant de jouets lui a remis le croquis d’une de leurs maisons de poupée. Il présente aux élèves le croquis en s’attardant à ses dimensions et au fait qu’il est composé de prismes rectangulaires.
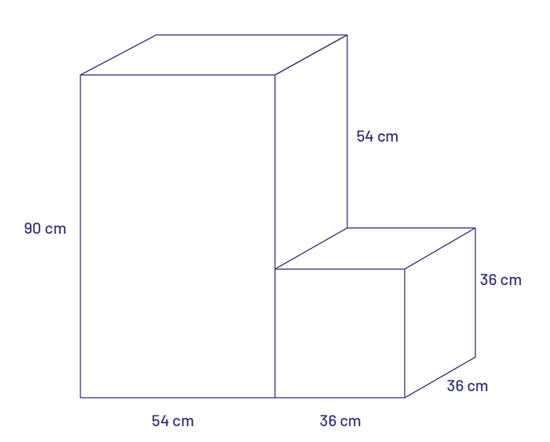 image Deux
blocs de différentes grandeurs sont posés l’un collé sur l’autre.Les mesures du premier sont :Hauteur : 90
centimètres,Largeur de la base : 54 centimètres.Les mesures du deuxième sont :Hauteur : 36 centimètres, longueur 36
centimètres, largeur 36 centimètres.La différence de hauteur entre les 2 blocs est de 54 centimètres.
image Deux
blocs de différentes grandeurs sont posés l’un collé sur l’autre.Les mesures du premier sont :Hauteur : 90
centimètres,Largeur de la base : 54 centimètres.Les mesures du deuxième sont :Hauteur : 36 centimètres, longueur 36
centimètres, largeur 36 centimètres.La différence de hauteur entre les 2 blocs est de 54 centimètres.
Ensuite, le personnel enseignant les invite à créer une maquette de cette maison qui comporte des mesures réduites de moitié (le rapport entre les mesures de la maquette et celles du croquis est de 1 à 2). Selon les habiletés des élèves et les matériaux disponibles, d’autres rapports peuvent être donnés pour réaliser la maquette; par exemple, les mesures sont réduites au quart (rapport \(1\;:\;4\)), aux 2 tiers (rapport \(2\;:\;3\)) ou même doublées (rapport \(2\;:\;1\)).
Après avoir formé des équipes de 2, le personnel enseignant leur distribue de grandes feuilles cartonnées (par exemple, carton bristol), des ciseaux, des règles, de la colle et du ruban-cache ou ruban adhésif, et leur alloue suffisamment de temps pour accomplir la tâche demandée (du temps peut aussi être accordé pour la décoration, si possible). Afin d’effectuer la tâche, les élèves peuvent tracer sur de grandes feuilles cartonnées le développement des 2 prismes à base rectangulaire. Ensuite, elles et ils les découpent et construisent leur maquette.
La tâche terminée, le personnel enseignant anime un échange en groupe classe qui met en valeur les diverses stratégies utilisées pour construire les maquettes.
Note : Cette activité pourrait être réalisée en se basant sur d’autres sortes de plans tels que le plan d’un pont, d’une tour, d’une machine simple ou d’un aménagement paysager.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 108-109.
Activité 2 : jeu d’association
Demander aux élèves de créer des cartes représentant des taux et rapports équivalents avec des images.
Préparer des cartes avec le taux ou le rapport écrit symboliquement. Par exemple, \(2\;:\ 10\), \(1\;:\ 5\), \(5\$\;/\ 15\), etc.
Distribuer une carte aux élèves et leur demander de circuler pour trouver la carte qui représente le même taux ou le même rapport.
Ce jeu pourrait aussi être placé dans un centre d’apprentissage.
Activité 3 : rapports équivalents
Il importe que les élèves comprennent ce qu’est un rapport équivalent. Si les élèves ne font qu’apprendre à faire des calculs, elles et ils ne développeront pas une compréhension de ce concept.
Par exemple 4 : 5 est équivalent au rapport 8 : 10. Les élèves doivent comprendre non seulement la relation multiplicative entre les 2 rapports, mais comprendre ce qu’ils représentent. S’il y a 4 pommes rouges pour 5 pommes vertes, il doit y avoir 8 pommes rouges pour 10 pommes vertes.
Pour vérifier et observer si les élèves comprennent le concept de rapport équivalent, leur demander de représenter soit avec du matériel de manipulation ou par un schéma pourquoi 4 : 5 n’est pas équivalent à 5 : 6 ou pourquoi 4 : 5 est équivalent à 12 : 15.
Activité 4 : rapports de fruits
Présenter cette situation de fruits aux élèves.
Les élèves peuvent créer et représenter un rapport à partir d’un ensemble de fruits. S’il y a 15 fruits (10 poires et 5 bananes), elles et ils peuvent faire des rapports tels que :
- 10 poires pour 5 bananes ou \(10:\;\;\;\;5\;\;{\rm{ou}}\;\;\frac{10}{5}\)
- 5 bananes pour 15 fruits ou \(5\;:\;\;\;15\;\;{\rm{ou}}\;\;\frac{5}{{15}}\)
- 10 poires pour 15 fruits ou \(10\;:\;\;\;15\;\;{\rm{ou}}\;\;\frac{{10}}{{15}}\)

Les élèves en 5e année apprennent aussi la notion de rapports ou taux équivalents. Dans l’exemple des fruits ci-dessus, on peut représenter les rapports mentionnés ci-haut par des rapports équivalents. Cette notion de rapports équivalents développe le raisonnement proportionnel.
- 10 poires pour 5 bananes ou \(10:\;\;\;5\;\;\;{\rm{ou}}\;\;\;\frac{{10}}{5}\;\;\;{\rm{ou}}\;\;\;\frac{2}{1}\) puisqu’on peut dire que pour chaque ensemble de 2 poires, il y a 1 banane.
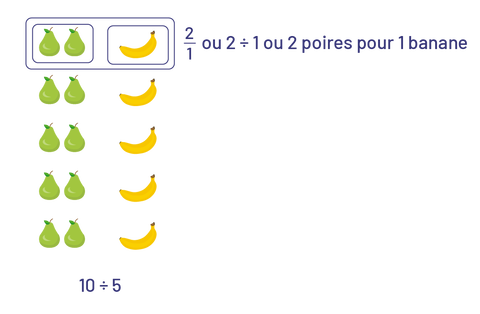 image Les
poires sont disposées en 2 colonnes de 5.Les bananes sont disposées en une colonne de 5.Un ensemble de 2 poires et un
ensemble d’une banane sont créés. Ces 2 ensembles sont mis ensemble pour créer un nouvel ensemble. Cet ensemble
représente la fraction suivante, 2 sur un ou 2 divisé par un ou 2 poires pour une banane.Dix divise 5.
image Les
poires sont disposées en 2 colonnes de 5.Les bananes sont disposées en une colonne de 5.Un ensemble de 2 poires et un
ensemble d’une banane sont créés. Ces 2 ensembles sont mis ensemble pour créer un nouvel ensemble. Cet ensemble
représente la fraction suivante, 2 sur un ou 2 divisé par un ou 2 poires pour une banane.Dix divise 5.
- 5 bananes pour 15 fruits ou \(5:\;\;\;15\;\;\;{\rm{ou}}\;\;\;\frac{5}{{15}}\;\;\;{\rm{ou}}\;\;\;\frac{1}{3}\) puisqu’on peut dire qu’il y a 1 banane pour chaque ensemble de 3 fruits.
 image Les
bananes sont disposées en une colonne de 5.Les poires sont disposées en 2 colonnes de 5.Une banane forme un ensemble.
Un nouvel ensemble est créé avec cette banane et 2 poires.Cet ensemble représente la fraction suivante :Un tiers, ou
un divisé par 3, ou une banane pour 3 fruits.5 divisé par 15.
image Les
bananes sont disposées en une colonne de 5.Les poires sont disposées en 2 colonnes de 5.Une banane forme un ensemble.
Un nouvel ensemble est créé avec cette banane et 2 poires.Cet ensemble représente la fraction suivante :Un tiers, ou
un divisé par 3, ou une banane pour 3 fruits.5 divisé par 15.
- 10 poires pour 15 fruits ou \(10\;:\;15\;\;\;{\rm{ou}}\;\;\;\frac{{10}}{{15}}\;\;\;{\rm{ou}}\;\;\frac{2}{3}\) puisqu’on peut dire qu’il y a 2 poires pour chaque ensemble de 3 fruits.
 image Les
poires sont disposées en 2 colonnes de 5.Les bananes sont disposées en une colonne de 5.Un ensemble de 2 poires est
créé, puis un nouvel ensemble est fait avec ces poires et une banane.Cet ensemble représente la fraction suivante :2
sur 3, ou 2 divisé par 3, ou 2 poires pour 3 fruits.
image Les
poires sont disposées en 2 colonnes de 5.Les bananes sont disposées en une colonne de 5.Un ensemble de 2 poires est
créé, puis un nouvel ensemble est fait avec ces poires et une banane.Cet ensemble représente la fraction suivante :2
sur 3, ou 2 divisé par 3, ou 2 poires pour 3 fruits.
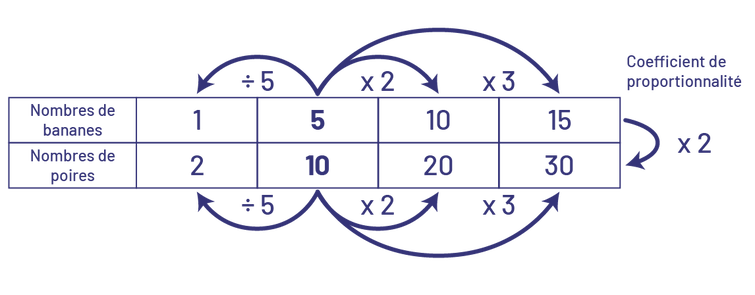
Nous pouvons représenter des rapports bananes : poires à l’aide d’un tableau de rapports.
Dans ce tableau, on peut également reconnaître qu’il existe une relation de proportionnalité entre le nombre de bananes et le nombre de poires, soit \( \times \;2\). Le coefficient de proportionnalité est de 2. On multiplie le nombre de bananes par 2 pour obtenir le nombre de poires.
 Il y a 5
bananes pour dix poires, si on divise par 5 on obtient une banane pour 2 poires. Si on multiplie par 2, on obtient dix
bananes pour 20 poires. Si on multiplie par 3, on obtient 15 bananes pour 30 poires.Le coefficient de proportionnalité
est de « fois 2. »
Il y a 5
bananes pour dix poires, si on divise par 5 on obtient une banane pour 2 poires. Si on multiplie par 2, on obtient dix
bananes pour 20 poires. Si on multiplie par 3, on obtient 15 bananes pour 30 poires.Le coefficient de proportionnalité
est de « fois 2. »
On peut donc dire que les rapports équivalents sont :
\(\frac{1}{2}\; = \frac{5}{{10}}\; = \frac{{10}}{{20}}\; = \;\frac{{15}}{{30}}\) ou \(1:\;\;\;2\; = \;5:\;\;\;10\; = \;15:\;\;\;30\).
