B1.2 Comparer et ordonner les nombres naturels jusqu’à 100 000, dans divers contextes.
Habileté : comparer et ordonner des nombres naturels jusqu’à 100 000
Des nombres repères peuvent être utilisés pour comparer des quantités. Par exemple, 41 132 est inférieur à 50 000 et 62 000 est supérieur à 50 000, donc 41 132 est inférieur à 62 000.
Les nombres peuvent être comparés à l’aide de leur valeur de position. Par exemple, lors de la comparaison de 82 500 et 84 500, la plus grande valeur de position dans laquelle les nombres diffèrent est comparée. Dans cet exemple, 2 unités de 1 000 (de 82 500) et 4 unités de 1 000 (de 84 500) sont comparées. Puisque 4 unités de 1 000 est supérieur à 2 unités de 1 000, 84 500 est supérieur à 82 500.
Les nombres peuvent être comparés en faisant appel au raisonnement proportionnel. Par exemple, 100 000 est 10 fois supérieur à 10 000; il est également 100 fois supérieur à 1 000. Il faudrait 1 000 billets de 100 dollars pour faire 100 000 $.
Selon le contexte du problème, les nombres peuvent être comparés de manière additive ou multiplicative.
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
La droite numérique est un modèle auquel les élèves doivent être exposés. La droite numérique ne représente pas la quantité correspondant aux nombres qui sont placés sur cette droite; elle permet de « voir » les nombres en relation les uns avec les autres. Par exemple, une droite numérique sur laquelle les nombres 50 001, 50 015, 50 100 et 50 500 sont placés représente la relation d’ordre entre ces nombres.
Source: Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 11.

Le développement du sens du nombre au cycle moyen est lié à la reconnaissance des relations entre les nombres, entre autres :
- relations de valeur de position;
- relations d’ordre;
- relations de proportionnalité
L’exploration de ces relations aide les élèves à comparer les nombres.
Voici quelques exemples de chacune.
Si on demande aux élèves de trouver des ressemblances, des différences et des liens entre les nombres 12, 24, 25, 37, 50, 96, 106 et 120, ils peuvent faire ressortir :
- que tous ces nombres, sauf 106 et 120, sont formés de 2 chiffres ou que 24 et 25 ont le même nombre de dizaines (relations de valeur de position);
- que le nombre 120 est le plus grand nombre ou que 24 est un peu moins que 25 (relations d’ordre);
- que 24 est le double de 12 ou que 25 est la moitié de 50 (relations de proportionnalité).
Relations d’ordre
L’habileté à reconnaître des relations d’ordre s’acquiert en comparant des nombres, en les plaçant en ordre croissant et décroissant, en comptant à rebours et en analysant la proximité relative de 2 nombres.
Au cycle moyen, les élèves doivent reconnaître la relation d’ordre entre les nombres en les comparant. Elles et ils peuvent décrire la relation en précisant, par exemple, que 350 est plus petit que 432. Voici quelques exemples de stratégies qu’elles et ils peuvent utiliser pour comparer de grands nombres.
| Les élèves peuvent reconnaître que 23 942 est plus grand que 12 273 : | Exemple |
|---|---|
| en ciblant une partie plus importante de chaque nombre; | Constater que 23 000 est plus grand que 12 000. |
| en visualisant les quantités importantes; |
Visualiser 23 regroupements de 1 000 et 12 regroupements de 1 000.  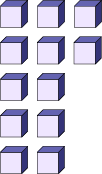 |
| en situant les nombres sur une droite numérique; | 
Le nombre 23 942 est situé à la droite du nombre 12 273. |
| en comparant les chiffres dans les diverses positions en partant de la gauche. | 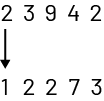
Le 2 représente 20 000 alors que le 1 représente 10 000. |
Afin d’aider les élèves à développer l’habileté à reconnaître les relations d’ordre entre les grands nombres, le personnel scolaire peut, à partir d’un nombre donné, leur demander de compter par 1 (par exemple, 12 998, 12 999, 13 000, 13 001…) ou par intervalles (par exemple, 32 200, 32 400, 32 600…) et de compter à rebours par 1 (par exemple, 26 271, 26 270, 26 269…) ou par intervalles (par exemple, 45 650, 45 600, 45 550…).
Ces activités aident les élèves à reconnaître qu’en comptant par 1 ou par intervalles, tout nombre nommé est supérieur à ceux qui le précèdent et inférieur à ceux qui le suivent, alors qu’en comptant à rebours par 1 ou par intervalles, tout nombre nommé est inférieur à ceux qui le précèdent et supérieur à ceux qui le suivent. Bien que ces relations puissent sembler évidentes aux adultes, les élèves, pour leur part, se trompent souvent, car elles et ils ne tiennent pas compte du concept de regroupement. Par exemple, lorsqu’on leur demande quel nombre précède 300, plusieurs ont tendance à répondre spontanément 399 parce que leur attention est portée sur les deux 0; elles et ils savent qu’un nombre qui se termine avec deux 0 est toujours précédé d’un nombre qui se termine par deux 9, mais oublient de tenir compte du regroupement par centaines. En revanche, lorsque le même problème est posé en contexte, les élèves sont davantage portés à donner des réponses réfléchies. Par exemple, dans une situation où un enfant a 300 cartes de hockey et qu’il en perd une, les élèves répondront facilement qu’il lui reste 299 cartes.
Les erreurs liées au concept de regroupement sont aussi fréquentes lors d’arrondissements pour lesquels il est nécessaire de cerner un intervalle. Par exemple, certains élèves diront que 12 497 se situe entre 12 490 et 12 400 au lieu de 12 500. L’utilisation d’un abaque ou d’un odomètre maison (créé à l’aide d’un rouleau de papier hygiénique et du gabarit) aide les élèves à comparer les nombres, à compter par intervalles et à découvrir les changements reliés aux regroupements par dizaines, par centaines…


Une fois que les élèves maîtrisent les relations « plus grand que » et « plus petit que », elles et ils doivent apprendre à préciser ces relations en faisant appel à leur compréhension du concept de quantité. Elles et ils emploient alors des expressions telles que près de, environ, la même chose que, beaucoup plus que et un peu moins que. Par exemple, les élèves peuvent dire que la population d’un village de 15 239 habitants est d’environ 15 000 habitants; que 304 est un peu plus que 300; que 12 894 est un peu moins que 13 000; que 32 523 contient environ une centaine de plus que 32 432 et que 620 et 618 sont plus près l’un de l’autre que 630 et 680.
Cette habileté à préciser les relations d’ordre entre les nombres prend toute son importance lorsque les élèves utilisent les nombres en contexte de résolution de problèmes, d’arrondissement, d’estimation et de comparaison. L’activité suivante permet aux élèves de démontrer cette habileté.
Tracer au tableau une droite numérique pour représenter un intervalle quelconque (par exemple, de 1 000 à 2 000). Placer quelques lettres (par exemple, A, B, C, D) dans cet intervalle tel qu’illustré ci-dessous.

Demander à quelques élèves de venir situer certains nombres sur la droite (par exemple, 1 873, 1 332, 1 167). Leur demander ensuite de décrire des relations d’ordre qui existent entre les nombres et les lettres.
Les élèves pourraient, par exemple, dire :
- que 1 167 se situe entre A et B;
- que les lettres B et C se situent entre 1 167 et 1 332;
- que le nombre 1 873 est plus près de 2 000 que de la lettre D;
- que la lettre B semble être plus au centre de l’intervalle entre 1 000 et 1 500 que la lettre C.
Source: Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 43-48.
