B1.3 Représenter des fractions équivalentes à partir des demis jusqu’aux douzièmes, y compris des fractions impropres et des nombres fractionnaires, à l’aide d’outils appropriés, dans divers contextes.
Habileté : représenter des fractions équivalentes à partir des demis jusqu’aux douzièmes, y compris des fractions impropres et des nombres fractionnaires, à l’aide d’outils appropriés
Reconnaître l’égalité de 2 fractions, c’est reconnaître que les 2 fractions représentent la même quantité. Selon Van de Walle et Folk (2005, p. 236 et 237), il faut faire la distinction entre le concept de fractions équivalentes et l’algorithme qui permet de déterminer des fractions équivalentes.
Concept : 2 fractions sont équivalentes si elles représentent la même quantité.
Algorithme : Pour obtenir une fraction équivalente à une fraction quelconque, il faut multiplier ou diviser son numérateur et son dénominateur par le même nombre (différent de 0).
La description de l’algorithme présentée ci-dessus ne permet pas de dégager le lien entre l’algorithme et le concept. Dans une classe où l’étude des mathématiques est fondée sur la résolution de problèmes et l’utilisation de représentations variées, les élèves développent une compréhension de l’algorithme à travers l’approfondissement de concepts. Ainsi, l’accent est mis sur la compréhension plutôt que sur l’application de procédures.
La notion de fractions équivalentes est abordée dès la 1re année. Toutefois, il est parfois difficile pour les élèves de saisir qu’une quantité peut porter plusieurs noms et être représentée par plusieurs nombres (par exemple, le nombre \(1\frac{2}{3}\) représente la même quantité que le nombre \(1\frac{6}{9}\); donc, on peut affirmer que \(1\frac{2}{3}\; = \;1\frac{6}{9}\)). La compréhension des fractions équivalentes fait partie du raisonnement proportionnel que les élèves vont continuer à développer aux cycles intermédiaire et supérieur.
Déterminer des fractions équivalentes, c’est déterminer des fractions qui représentent la même quantité. On cherche alors un nombre de « petites parties » d’un tout qui correspondent à un nombre particulier de « grandes parties » du même tout. Par exemple, si on cherche le nombre de seizièmes qui correspond à 1 et 1 quart (\(1\frac{1}{4}\; = \;\frac{?}{{16}}\)) :


\(1\frac{1}{4}\;\)d’une tablette de chocolat


\(1\frac{4}{{16}}\;\;{\rm{ou}}\;\frac{{20}}{{16}}\) de la même tablette de chocolat
Les seizièmes sont 4 fois plus petits que les quarts. Dans un tout, il y a donc 4 fois plus de seizièmes que de quarts \(\left( {4\; \times \;4\; = \;16} \right)\). Afin de représenter la même quantité, il doit y avoir 4 fois plus de parties identifiées \(\left( {4\; \times \;1\; = \;4} \right)\). Donc, 4 seizièmes c’est équivalent à 1 quart. Voilà ce qui explique l’algorithme ci-dessous.
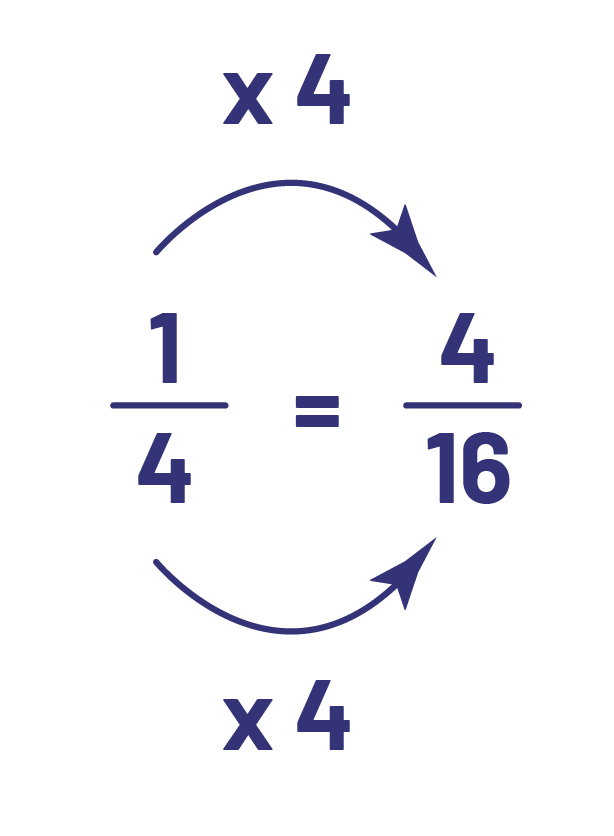
On peut voir que l’inverse est aussi vrai. Puisque les quarts sont 4 fois plus grands que les seizièmes, il en faut 4 fois moins \(\left( {16\; \div \;4\; = \;4} \right)\). Afin de représenter la même quantité, il doit y avoir 4 fois moins de parties identifiées \(\left( {4\; \div \;4\; = \;1} \right)\). Donc, 1 quart c’est équivalent à 4 seizièmes. Voilà ce qui explique l’algorithme ci-dessous.
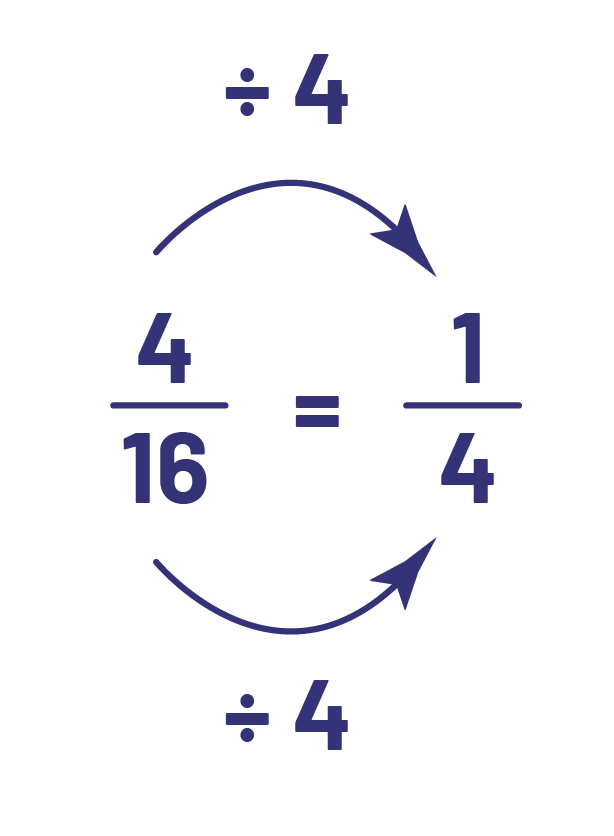
Il est essentiel que les élèves du cycle moyen comprennent et puissent expliquer cette relation afin de donner un sens à l’algorithme utilisé pour déterminer des fractions équivalentes.
Or, il n’est pas toujours aussi facile de reconnaître des fractions équivalentes. Prenons, par exemple, \(\frac{4}{6}\) et \(\frac{6}{9}\). On ne voit pas l’équivalence comme le résultat d’une multiplication du numérateur et du dénominateur par un nombre entier, soit l’algorithme usuel. On peut réduire chaque fraction à sa plus simple expression pour constater que chacune est équivalente à \(\frac{2}{3}\). On peut aussi faire appel à une représentation semi-concrète :
\(\frac{4}{6}\)

\(\frac{6}{9}\)

Cette représentation permet de voir l’aspect multiplicatif. On voit que les sixièmes sont une fois et demie plus grands que les neuvièmes. Pour passer des sixièmes aux neuvièmes, il faut donc 1,5 (\(1\frac{1}{2}\)) fois plus de morceaux. Cependant, ce type de situation est d’un niveau plus avancé que celui attendu au cycle moyen.
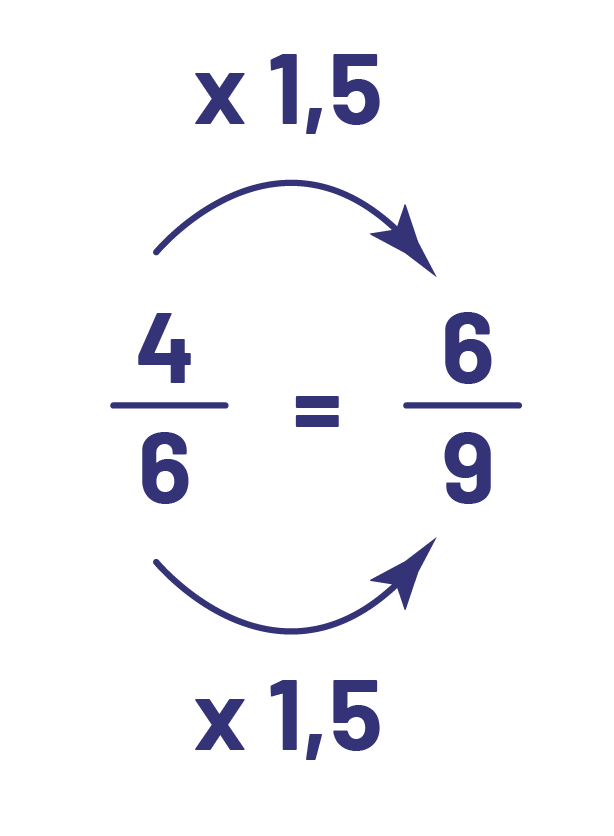
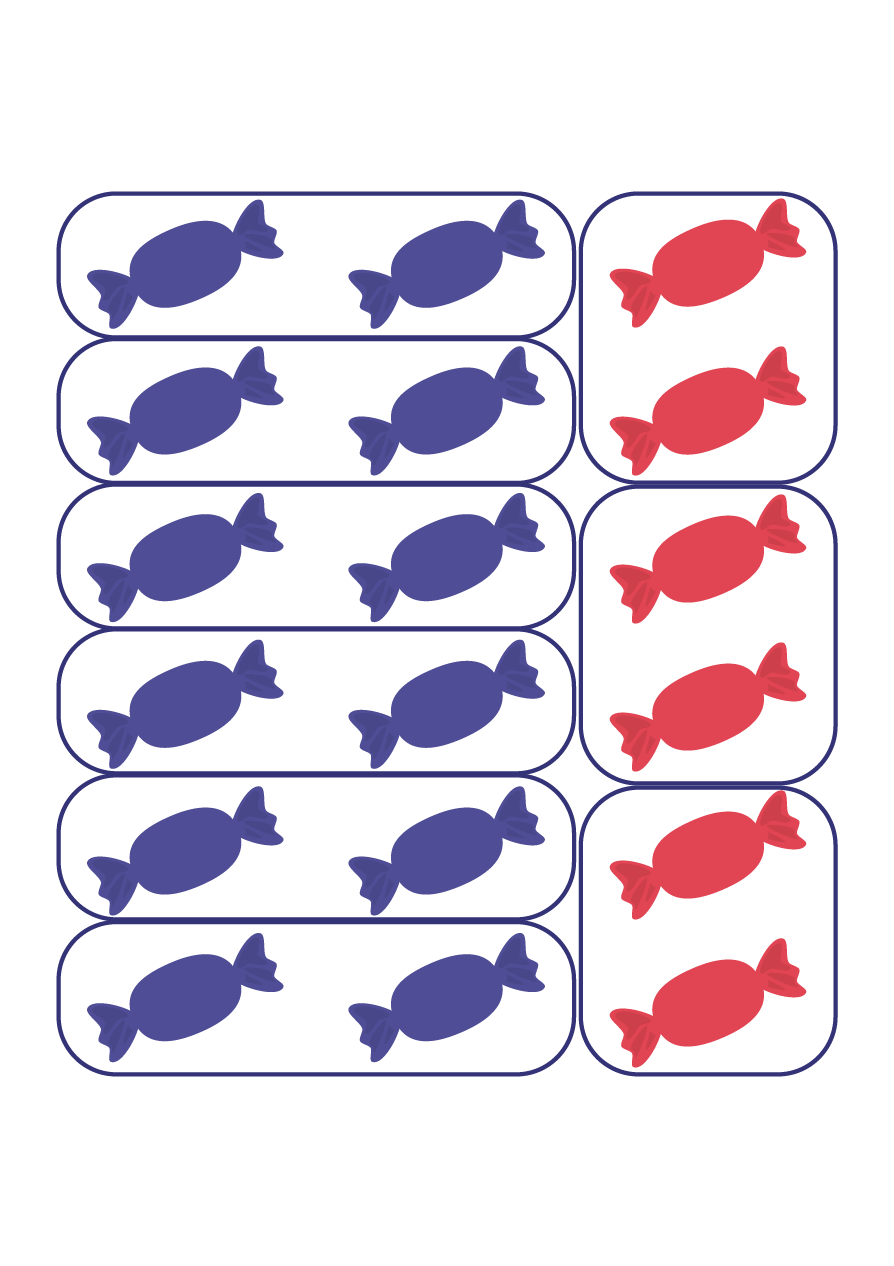
La relation d’équivalence doit aussi être explorée par rapport aux fractions d’un ensemble. Dans l’image ci-dessous, les élèves voient aisément que \(\frac{{12}}{{18}}\) des bonbons sont emballés dans des papillotes bleus.

Toutefois, ils ont de la difficulté à déterminer d’autres fractions équivalentes (par exemple, \(\frac{2}{3}\), \(\frac{4}{6}\), \(\frac{6}{9}\)). Il importe alors de présenter des activités qui leur permettent de manipuler les éléments de l’ensemble. Ainsi, les élèves peuvent les grouper en ensembles de 6, de 3 ou de 2 et déterminer des fractions équivalentes.
\(\frac{2}{3}\) des bonbons sont emballés dans des papillotes bleus

\(\frac{4}{6}\) des bonbons sont emballés dans des papillotes bleus
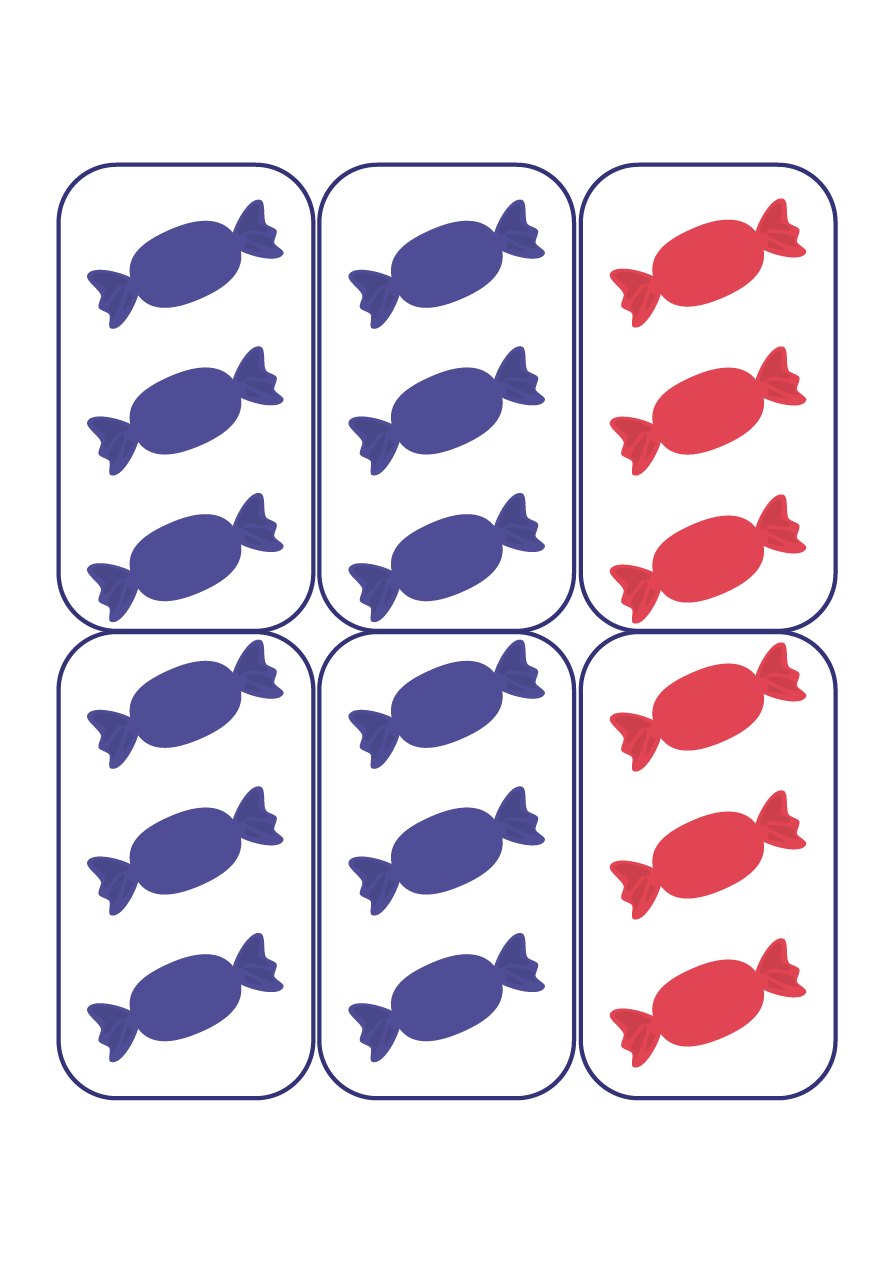
\(\frac{6}{9}\) des bonbons sont emballés dans des papillotes bleus
L’expérience concrète avec les fractions équivalentes est le fondement du raisonnement proportionnel. On ne saurait lui accorder trop d’importance. C’est pourquoi le personnel enseignant doit planifier des activités qui reposent sur les notions informelles reliées aux fractions équivalentes.
Quelques remarques s’imposent par rapport à l’apprentissage des fractions équivalentes. Premièrement, il ne faut pas mettre l’accent sur le concept de fraction irréductible. Il est préférable de traiter ces fractions comme toutes les autres et de mettre l’accent sur les fractions équivalentes, c’est-à-dire sur les fractions qui sont des représentations différentes d’une même quantité. Deuxièmement, il faut accorder de l’importance au vocabulaire que l’on utilise et à la compréhension qu’en ont les élèves, ainsi qu’au vocabulaire que les élèves utilisent et comprennent. Par exemple, des élèves affirment que \(\frac{3}{4}\) et \(\frac{9}{{12}}\) sont des fractions équivalentes, mais que \(\frac{3}{4}\) est plus grand ou plus petit que \(\frac{9}{{12}}\), ou même qu’il s’agit d’une « meilleure » fraction. De même, certains élèves pensent que la fraction \(\frac{2}{3}\) est plus petite que la fraction \(\frac{4}{6}\), puisque \(\frac{2}{3}\) a été obtenu lorsqu’on a « réduit » \(\frac{4}{6}\). Il est important de déterminer la source des méprises des élèves et de chercher à corriger toute conception erronée.
Source: Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 50-53.
Nombre fractionnaire et fraction impropre
L’apprentissage des fractions débute généralement avec l’utilisation de fractions propres, soit des fractions inférieures à 1. Au cycle moyen, les élèves rencontrent des fractions qui représentent des quantités supérieures à 1 (par exemple, en comptant des morceaux de tartes coupées en quarts, on peut compter 11 quarts qui restent). De telles situations les amènent aux fractions impropres (par exemple, \(\frac{{11}}{4}\)) et aux nombres fractionnaires (par exemple, \(2\frac{3}{4}\)).
Il est important que les élèves reconnaissent qu’un nombre fractionnaire et la fraction impropre correspondante représentent la même quantité et que chaque nombre fractionnaire peut être exprimé sous forme de fraction impropre et vice versa.
Exemple
Si on a \(2\frac{3}{4}\) tartes, on peut couper les 2 tartes en quarts, ce qui fait \(2\; \times \;4\) quarts, soit 8 quarts. Si on ajoute les 3 autres quarts, on obtient un total de 11 quarts, ou \(\frac{{11}}{4}\).
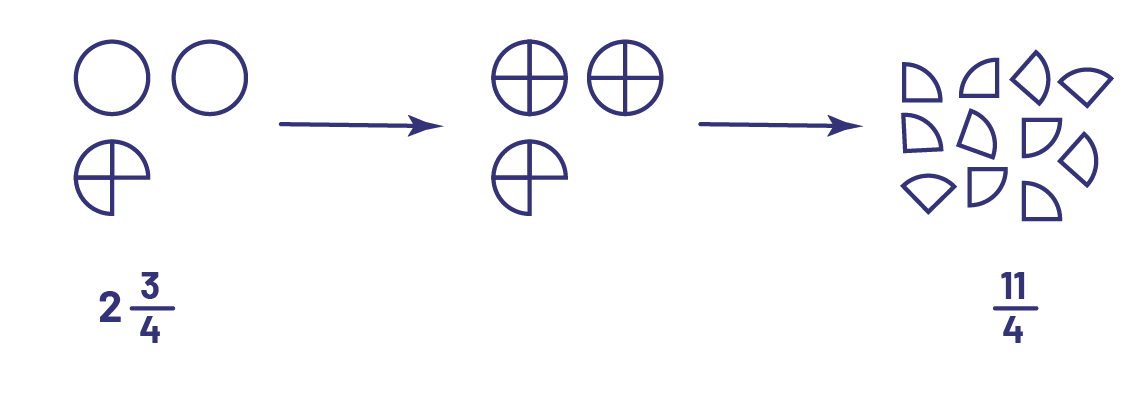
Si on a 11 quarts de tarte, on peut grouper les quarts de tartes, 4 à la fois, pour former des tartes entières. On peut ainsi former 2 tartes avec 8 morceaux. Il restera alors 3 quarts. On a donc \(2\frac{3}{4}\) tartes.
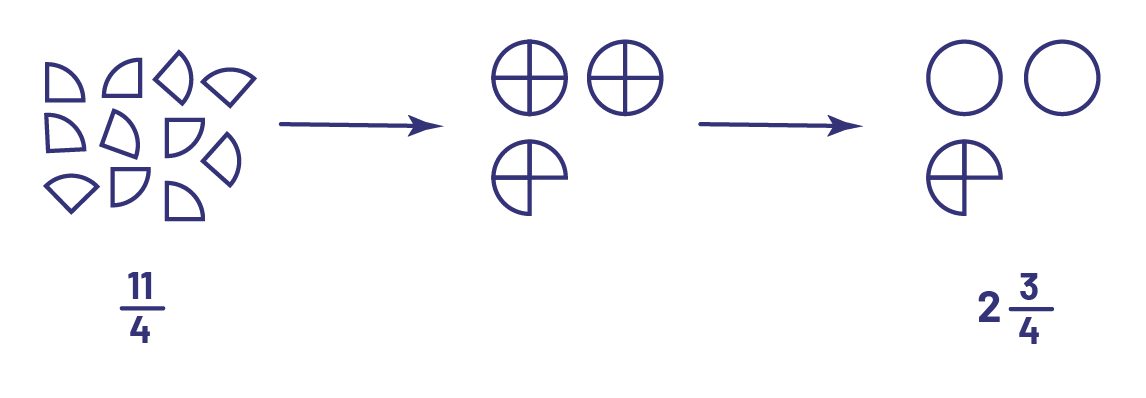 image 11 quarts de tartes, représentées par la fraction 11 sur 4. Cela donne 2 tartes et 3 quarts divisés en quarts. Cela donne 2 tartes entières et un 3 quarts de tarte., représenté par la fraction, 2 et 3 sur 4.
image 11 quarts de tartes, représentées par la fraction 11 sur 4. Cela donne 2 tartes et 3 quarts divisés en quarts. Cela donne 2 tartes entières et un 3 quarts de tarte., représenté par la fraction, 2 et 3 sur 4.
Il est important que les élèves puissent comprendre les relations entre les nombres en cause au lieu d’utiliser une procédure prescrite. Cette compréhension peut être développée en présentant des activités en contexte et en encourageant les élèves à représenter concrètement les situations. Ainsi, le personnel enseignant guide les élèves dans le développement de leur compréhension.
On devrait profiter du travail avec les fractions impropres pour faire des liens avec la division. On sait qu’une division, comme \(5\; \div \;2\), peut être exprimée de façon symbolique, par \(\frac{5}{2}\). Par exemple, 2 enfants veulent se partager 5 biscuits. Combien chacune ou chacun en recevront-elles ou ils? La réponse est \(2\frac{1}{2}\) biscuits chacune ou chacun. Ou encore, on a 5 biscuits qu’on veut placer dans des sacs, 2 par sac. Combien y aura-t-il de sacs? La réponse est \(2\frac{1}{2}\)sacs (2 sacs pleins et un sac à moitié plein). Dans les 2 exemples, la division de 5 par 2 (\(5\; \div \;2\)) peut être exprimée de façon symbolique par \(\frac{5}{2}\) et la réponse, soit \(2\frac{1}{2}\), peut aussi être exprimée par \(\frac{5}{2}\). L’expression numérique \(\frac{5}{2}\), dans ce contexte, a donc 2 sens, soit « 5 divisé par 2 » et « 5 demis ». De plus, l’exploration du nombre fractionnaire permet d’examiner le traitement du reste d’une division. Par exemple, si 4 amis veulent se partager 15 tablettes de chocolat, combien de tablettes auront-ils chacun? La division de 15 par 4 (\(15\; \div \;4\)) donne un reste de 3 qui sert dans la réponse \(3\frac{3}{4}\).
Source: Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 53-54.
Des modèles et des outils peuvent être utilisés pour développer la compréhension des fractions équivalentes.
Exemples
- Des bandes de fractions ou d’autres modèles, comme des cercles fractionnaires, peuvent créer la même aire que la fraction d’origine lorsqu’on utilise des parties fractionnées ou assemblées.
- Des bandes de papier peuvent être pliées pour montrer le fractionnement afin de créer des parties équivalentes.
- Une droite numérique double ou un tableau de rapports peut être utilisé pour représenter des fractions équivalentes basées sur différentes échelles.
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
Difficultés encourues par les élèves
Une fraction est une partie d’un tout. De façon plus abstraite, une fraction est aussi un nombre (par exemple, le nombre \(\frac{1}{2}\) représente la moitié du nombre 1). Elle représente donc une quantité. Cependant, cette quantité n’est pas composée seulement de valeurs entières (par exemple, une quantité de poires peut correspondre à \(\frac{1}{2}\) poire, une distance peut être de \(1\frac{3}{4}\) km, c’est-à-dire 1 km et une partie d’un autre). Les fractions offrent donc une précision supplémentaire que les nombres naturels ne peuvent donner.
Le développement du sens du nombre relié aux fractions représente un grand défi pour les élèves. Baroody et Coslick (1998, p. 9-13 et 9-14) tentent une explication et soulèvent certaines difficultés tant dans l’apprentissage que dans l’enseignement des fractions. Voici quelques-unes de ces difficultés.
- Les élèves ont du mal à se représenter des fractions selon divers modèles. Puisque l’enseignement des fractions se fait souvent à l’aide d’un seul modèle, par exemple en prenant un cercle ou une tarte, beaucoup d’élèves n’ont pas intégré le fait que pour obtenir une fraction, soit une partie d’un tout, il faut d’abord diviser ce tout en parties équivalentes.
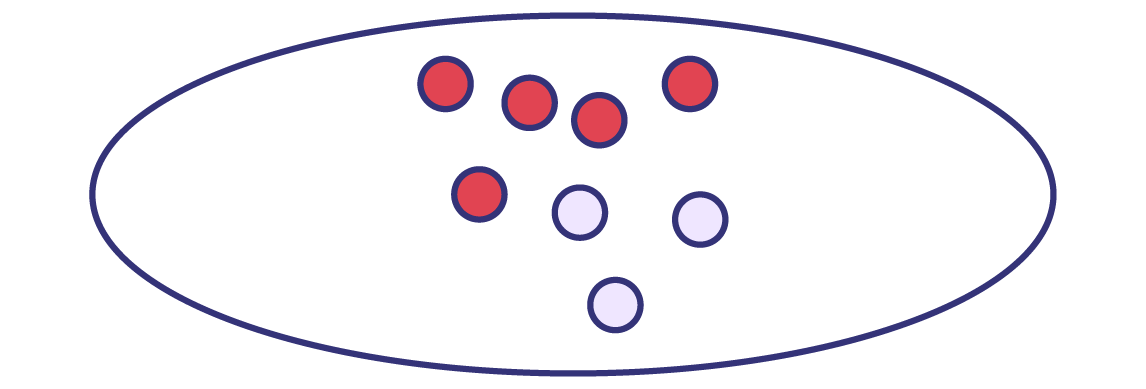
- Certaines et certains élèves comparent la partie d’un tout à la partie restante plutôt qu’au tout. Dans l’exemple qui suit, \(\frac{5}{8}\) de l’ensemble des billes sont roses. Mais, certains élèves représentent cette situation par la fraction \(\frac{5}{3}\).
- Les élèves ne développent pas un solide sens de la fraction puisque souvent, elles et ils ne voient pas le lien entre une fraction (par exemple, \(\frac{3}{4}\)) et la fraction unitaire correspondante (\(\frac{1}{4}\)), soit que \(\frac{3}{4}\; = \;\frac{1}{4}\; + \;\frac{1}{4}\; + \;\frac{1}{4}\) ou que \(\frac{3}{4}\; = \;3\; \times \;\frac{1}{4}\).
- Plusieurs élèves ne maîtrisent pas le concept de fractions équivalentes parce qu’elles et ils n’ont pas le bagage d’expériences suffisant pour comprendre la relation multiplicative qui caractérise ces fractions. En puisant dans leurs expériences passées avec les nombres naturels, il leur arrive de créer de fausses équivalences. Les élèves écrivent, par exemple,
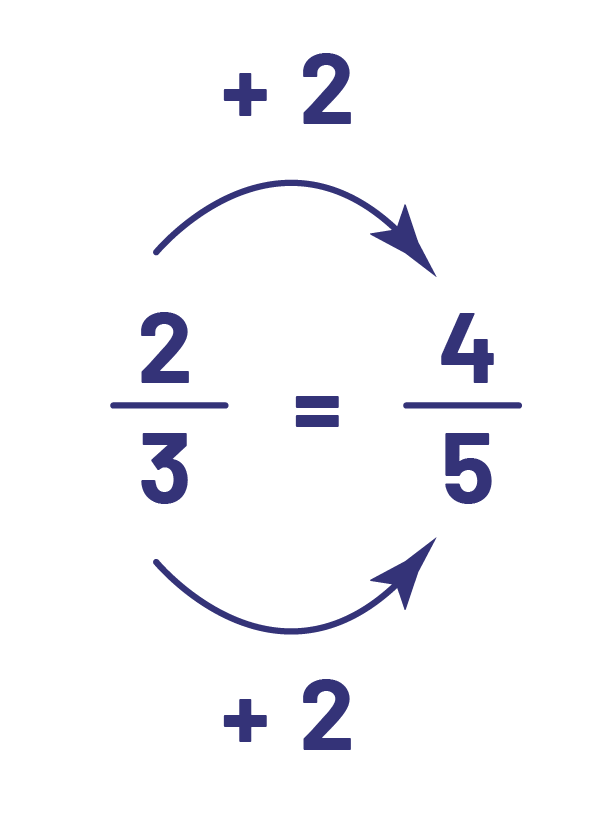 , ce qui est faux, au lieu de l’équivalence
, ce qui est faux, au lieu de l’équivalence 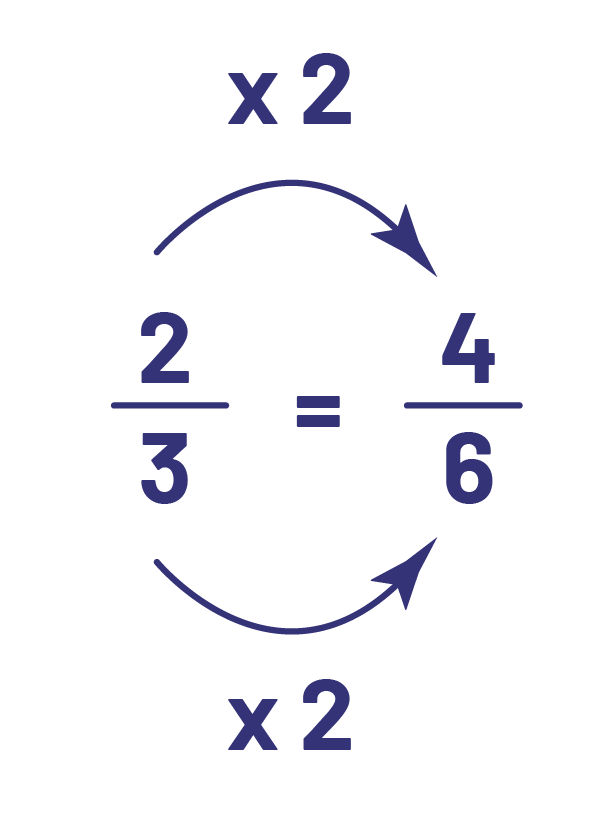 qui est vraie.
qui est vraie.
Source: Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 29-31.
Habileté : représenter des fractions dans divers contextes
Le contexte est constitué de l’ensemble des renseignements entourant une situation. Dans l’étude des fractions, le tout est une partie essentielle du contexte. En effet, une fraction comme \(\frac{2}{3}\), sans mention du tout, n’offre pas suffisamment d’information pour que la quantité correspondant à la fraction en contexte soit bien cernée. Par exemple, quand il est question de un demi, les gens conçoivent généralement que c’est peu. Pourtant, il faut considérer cette quantité en contexte – comme on le fait pour les nombres naturels – puisqu’on peut porter divers jugements sur une même fraction. Manger la moitié d’une pomme à la collation, c’est peu; manger la moitié d’une tarte, c’est beaucoup; si la moitié des élèves de la classe sont absents, c’est beaucoup. Le contexte est donc essentiel si on veut porter un jugement éclairé sur la quantité représentée par une fraction. Il est aussi important que les élèves apprennent à toujours tenir compte du tout. Une fraction n’a aucun sens si elle n’est pas mise en relation avec un tout. Par exemple, on ne peut comparer 1 demi-pizza et 1 tiers de pizza si elles n’ont pas la même superficie à moins que l’on nous présente les pizzas en question. Le personnel enseignant doit présenter des situations d’apprentissage qui permettent aux élèves de découvrir qu’une fraction ne révèle rien de la taille du tout ou de ses parties; elle nous renseigne seulement sur la relation qui existe entre un tout et ses parties.
Dans toute situation, le tout correspond à un élément ou à un ensemble d’éléments.
- Si le tout correspond à un élément, on peut le fractionner en parties équivalentes. Chacune des parties peut alors être comparée au tout.
Exemples

- Si le tout correspond à un ensemble d’éléments, soit une collection d’objets, quelques-uns des éléments peuvent être regroupés pour former une partie de l’ensemble et représenter ainsi une partie du tout.
Exemples
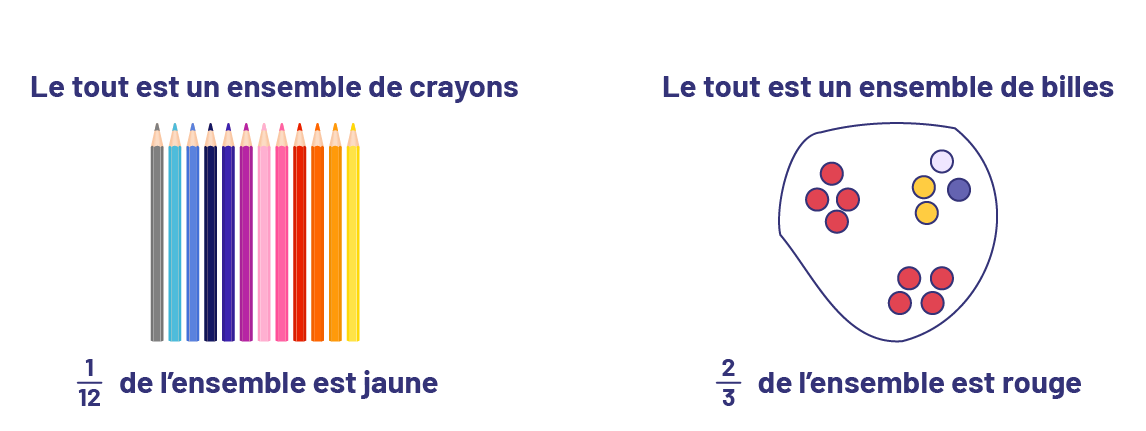
En général, lorsqu’il est question de fractions, on se réfère à 3 modèles de tout : le modèle d’ensemble, le modèle de longueur et le modèle de surface.
Source: Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 31-32.
Connaissance : fractions équivalentes
Les fractions équivalentes décrivent la même relation ou la même quantité.
- Lorsqu’on travaille avec des fractions en tant que quotient, les fractions équivalentes sont celles qui ont le même résultat que quand les numérateurs sont divisés par les dénominateurs.
- Lorsqu’on travaille avec des fractions comme parties d’un tout, les parties de la fraction peuvent être fractionnées ou assemblées pour créer des fractions équivalentes. Le tout ne change pas.
- Lorsqu’on travaille avec des fractions à titre de comparaison, le rapport entre le numérateur et le dénominateur des fractions équivalentes est égal.
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
Connaissance : fraction impropre
Une fraction impropre est une fraction où le numérateur est plus grand que le dénominateur. La fraction représente une quantité plus grande que l’unité.
Exemples
\(\frac{{11}}{3},\;\frac{5}{2},\;\frac{22}{{13}}\)
Connaissance : nombre fractionnaire
Un nombre fractionnaire est une fraction ayant un nombre entier ainsi qu’une fraction. La fraction représente une quantité plus grande que l’unité.
Exemples
\(2\frac{1}{2},\;12\frac{2}{5},\;5\frac{{10}}{{23}}\)
