B2.5 Additionner et soustraire des fractions ayant des dénominateurs communs, dans divers contextes.
Habileté : additionner et soustraire des fractions ayant des dénominateurs communs, dans divers contextes
Faire le lien entre les opérations sur les nombres naturels et celles sur les fractions
Les élèves ont déjà acquis une compréhension solide de l’addition et de la soustraction. Il est important de faire des liens entre les opérations sur les nombres naturels et celles sur les fractions. Par exemple, l’addition de 3 huitièmes et de 2 huitièmes est la même que celle de 3 bonbons et de 2 bonbons. Seule la notation est différente et plus complexe.
Valoriser les procédures informelles pour développer des stratégies
Il est important de valoriser les procédures informelles, car elles contribuent au développement du sens du nombre et du sens des opérations. Dans des situations qui impliquent des opérations, plusieurs élèves font appel à des algorithmes personnels plutôt qu’aux procédures. Par exemple, l’élève qui a un bon sens du nombre pourrait aborder l’addition de \(\frac{7}{8}\) d’un sandwich et de \(\frac{4}{8}\) d’un autre sandwich identique de cette façon : « Je sais qu’avec \(\frac{7}{8}\) d’un sandwich, il me manque \(\frac{1}{8}\) d’un sandwich pour avoir un sandwich complet. Alors, si j’ajoute \(\frac{1}{8}\) à \(\frac{7}{8}\), j’ai un entier et il me reste \(\frac{3}{8}\). Donc, \(\frac{7}{8}\; + \;\frac{4}{{8\;}}\; = \;1\frac{3}{8}\)».
Nature des opérations fondamentales
L’application d’une opération sur des nombres a pour effet de réorganiser les quantités en jeu. Il est très important que les élèves comprennent cette facette de la quantité lorsqu’elles et ils utilisent l’une ou l’autre des 4 opérations.
Les élèves du cycle moyen ont eu l’occasion d’apprendre cette relation par rapport aux 4 opérations sur les nombres naturels. Dans l’addition, 2 quantités sont mises ensemble pour former une nouvelle quantité. Dans une soustraction, on enlève une quantité d’une autre. On peut aussi reconnaître que l’on cherche une quantité par laquelle 2 quantités données diffèrent. Toutefois, que l’on ajoute, compare, réunisse ou sépare, il est important de connaître et de comprendre que l’opération a un effet sur les quantités.
Lorsque des fractions sont en jeu, il devient encore plus important de s’attarder au sens de l’opération, de choisir un modèle approprié et de réfléchir aux quantités. Il faut beaucoup de temps pour construire un sens des opérations sur les fractions, car il faut réfléchir aux numérateurs, aux dénominateurs et aux touts en cause. Il faut donner aux élèves l’occasion de travailler avec des modèles concrets et semi-concrets et de développer un sens de l’ordre de grandeur des résultats avant de passer aux opérations mettant en cause les représentations symboliques.
Addition et soustraction
Selon le programme-cadre, les élèves de 5e année voient l’addition et la soustraction de fractions ayant un dénominateur commun. Il s’agit essentiellement de l’addition et de la soustraction d’objets ou de quantités de même nature. Par exemple, dans \(\frac{3}{7}\; + \;\frac{2}{7}\; = \;\frac{5}{7}\), l’addition représente simplement 3 septièmes + 2 septièmes = 5 septièmes, tout comme 3 pommes + 2 pommes = 5 pommes. Dans cet exemple, les septièmes sont comptés de la même façon que des pommes. On a 3 morceaux d’une certaine taille et 2 morceaux de la même taille, ce qui donne 5 morceaux de cette taille. Effectuer l’addition de fractions devient plus complexe lorsque les fractions ont des dénominateurs différents, puisque les morceaux n’ont pas la même taille et ne sont pas de même nature. Ces opérations sont étudiées en 6e année.
La soustraction se traite de la même façon. Par exemple, si j’enlève 3 billes d’un sac qui en contient 5, il en reste 2. De même, si je soustrais 3 huitièmes de 5 huitièmes, il reste 2 huitièmes (\(\frac{5}{8}\; - \;\frac{3}{8}\; = \;\frac{2}{8}\)).
L’addition de 2 nombres naturels a pour effet d’augmenter les 2 quantités initiales, tandis que la soustraction de 2 nombres naturels a pour effet de diminuer la quantité initiale. Il est important que les élèves comprennent qu’il en est de même pour l’addition et la soustraction de fractions. Cela leur permet de comprendre l’invraisemblance de certaines réponses obtenues à partir de procédures erronées. Par exemple, l’élève qui, pour calculer \(\frac{2}{3}\; + \;\frac{1}{3}\), additionne les numérateurs et les dénominateurs et obtient \(\frac{3}{6}\), devrait voir que cette réponse, qui est égale à \(\frac{1}{2}\), est inférieure à une des fractions initiales, soit \(\frac{2}{3}\).
Description de la vidéo
Description à venir
Explorer les opérations à l’aide de plusieurs modèles
Il est important pour les élèves d’apprendre les concepts liés aux fractions dans diverses situations à l’aide d’une variété de modèles tels que des modèles de surface et des modèles de longueur. Il en est de même pour l’apprentissage des opérations sur les fractions.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 75-77.
Lorsqu’on travaille avec les fractions, le plus important et parfois le plus difficile, c’est de bien représenter le tout. En 5e année, les élèves additionnent et soustraient des fractions ayant des dénominateurs communs. Avec du matériel concret ou semi-concret, l’effet visuel de l’addition et de la soustraction est renforcé. En puisant dans leurs expériences avec les nombres naturels et en se forgeant un sens de l’opération, les élèves peuvent reconnaître, par exemple, que l’ajout de 2 tiers (\(\frac{2}{3}\)) à 1 tiers (\(\frac{1}{3}\)) donne 3 tiers (\(\frac{3}{3}\)), soit le tout.
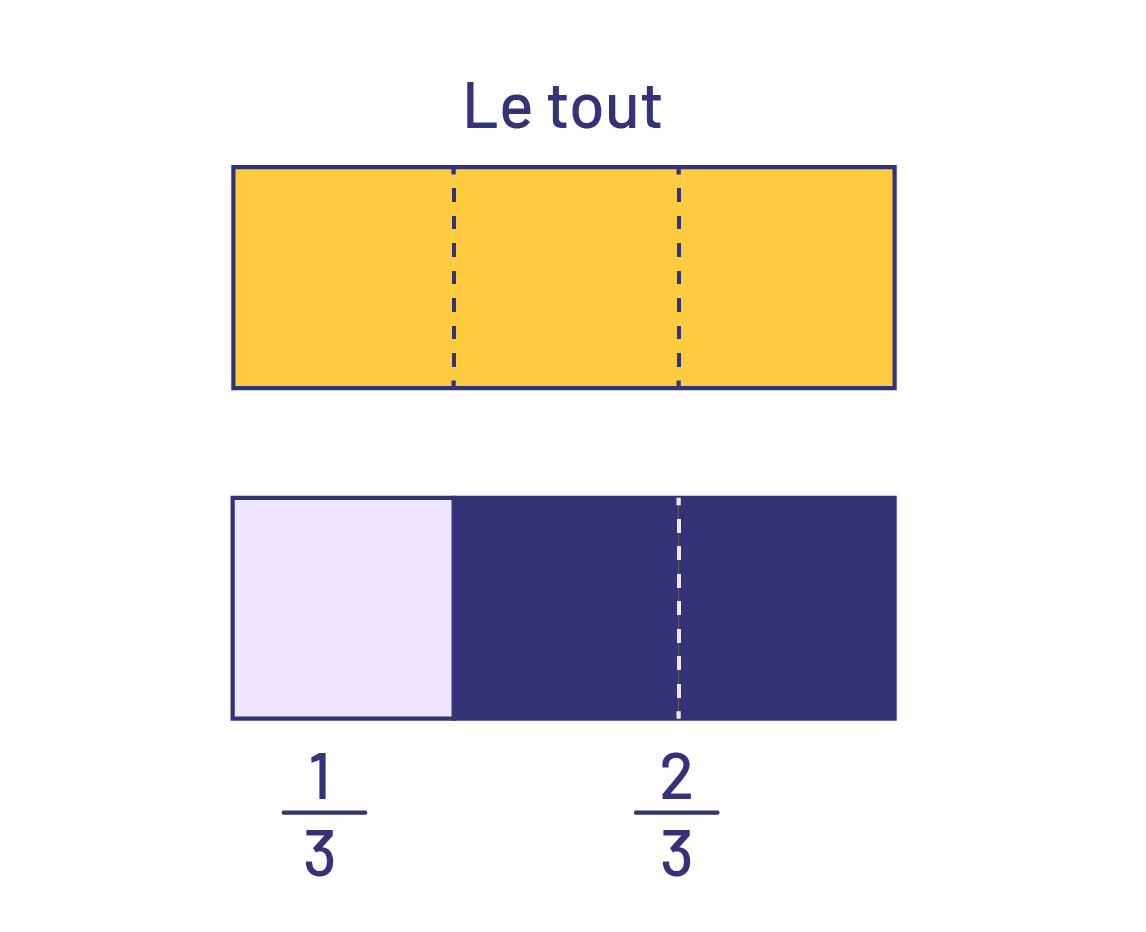
Or, il n’est pas toujours clair pour les élèves que l’addition se fait par rapport au numérateur. Dans une situation où il reste 3 huitièmes (\(\frac{3}{8}\)) d’une pizza et 2 huitièmes (\(\frac{2}{8}\)) d’une autre pizza de même grandeur, on cherche combien il en reste en tout. Est-ce qu’on compte des huitièmes ou des seizièmes, puisque les pizzas comptaient 16 morceaux en tout?
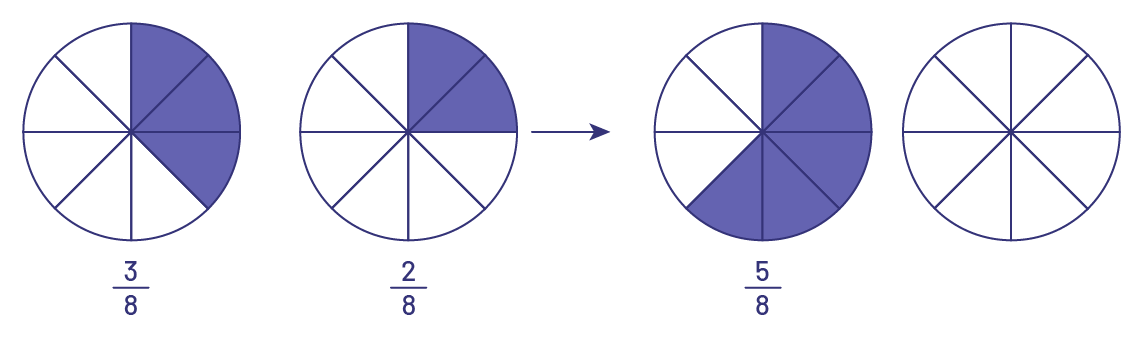image Deux cercles divisés en 8 parties égales, représentent les fractions, 3 sur 8 et 2 sur 8. Le premier cercle a 3 parties ombragées, le deuxième cercle a 2 parties ombragées.Une flèche pointe vers 2 autres cercles. Ils sont eux aussi divisés en 8 parties égales. Un de ces cercles a 5 parties ombragées, cela représente la fraction 5 sur 8.
Les élèves doivent aussi explorer des situations comprenant des fractions impropres. Par exemple, l’opération \(\frac{{10}}{4}\; + \;\frac{3}{4}\) pourrait être représentée à l’aide du modèle suivant.
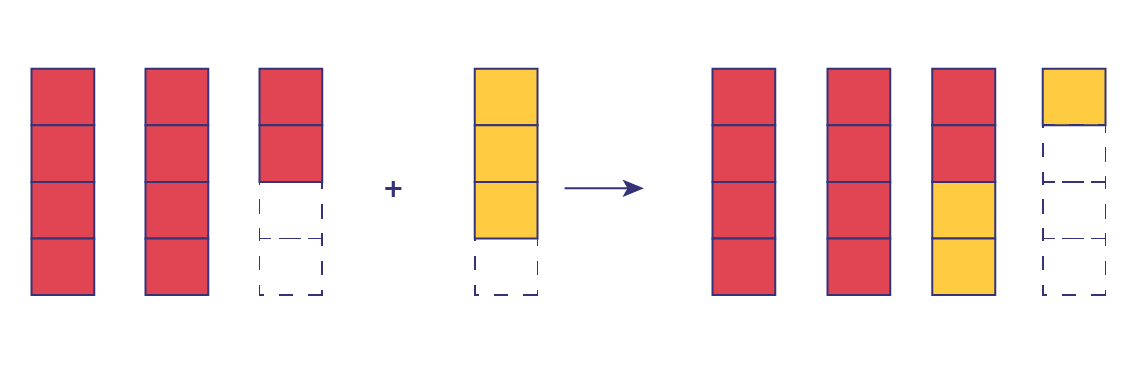image 2 rectangles composés de 4 espaces remplis en rouge et un troisième rectangle dont 2 espaces sont en rouge. Les deux autres espaces de ce rectangle sont vides. On additionne un rectangle identique, 3 de ces espaces sont remplis en jaune, le quatrième est vide. Une flèche nous pointe vers une modification. Il y a toujours 4 rectangles, 2 sont complètement rouges, le troisième a 2 parties en rouge et 2 parties en jaune. Le quatrième a une partie jaune.
Ce modèle permet d’exprimer le résultat sous la forme \(\frac{{13}}{4}\) ou \(3\frac{1}{4}\).
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 92-94.
Exemples
Problèmes d’ajout
Mila a mangé \(\frac{2}{8}\) d’un sous-marin, alors que Pierre en a mangé \(\frac{3}{8}\). Quelle fraction du sous-marin a été mangée par les 2 enfants?
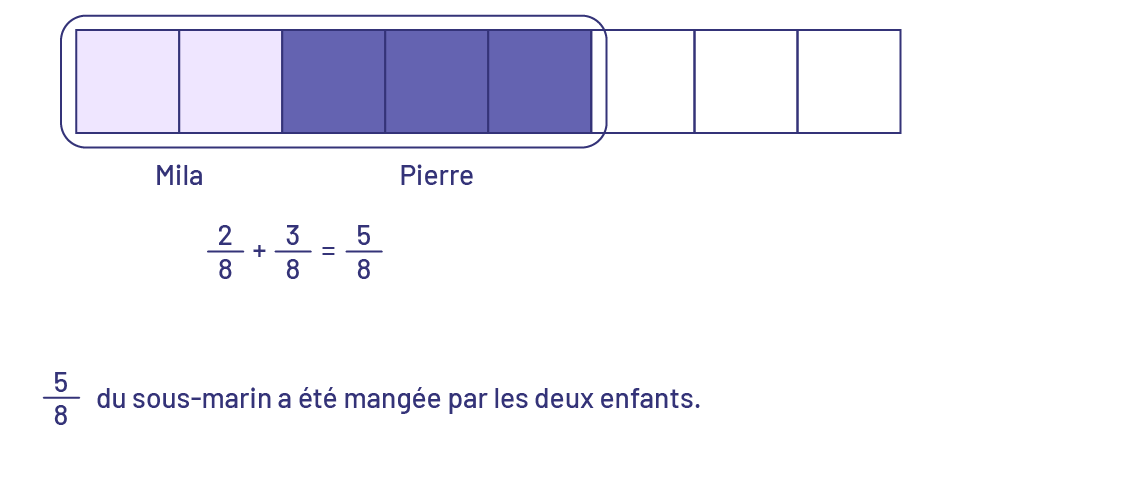
Problème de comparaison
Mila a pris \(\frac{2}{8}\) d’un pichet d’eau pour arroser sa plante. Pierre a pris \(\frac{5}{8}\) du pichet pour arroser la sienne. Quelle fraction représente la différence entre les quantités d’eau utilisées par Pierre et Mila?
Cette situation se traduit par \(\frac{5}{8}\; - \;\frac{2}{8}\; = \;\frac{3}{8}\).
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 78.
image Droite numérique de zéro à un, graduée en 8 intervalles réguliers.Des bonds de 2 intervalles représentent la fraction de Mila, 2 sur 8.Un bond de 5 intervalles représente la fraction de Pierre 5 sur 8.La différence est représentée par un bond de 3 intervalles et la fraction, 3 sur 8.
Il y a une différence de \(\frac{3}{8}\) d’eau du pichet utilisé par Pierre et Mila.
Connaissance : numérateur
Nombre de parties équivalentes du tout dont se compose la fraction.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 34.
Le numérateur est le nombre en haut de la fraction. Son rôle nous permet de connaître le nombre de parties équivalentes ou de groupes dont il s’agit.
Connaissance : dénominateur commun
Nombre de parties équivalentes par lequel le tout est divisé.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 34.
Le dénominateur est le nombre qui se trouve en bas de la fraction. Ce nombre nous permet de savoir combien il y a de parties équivalentes dans le tout. Lorsque le dénominateur est commun, ceci signifie que les 2 dénominateurs sont identiques.