B1. Sens du nombre
Démontrer sa compréhension des nombres et établir des liens avec leur utilisation dans la vie quotidienne.
Situation d’apprentissage 1 : visez juste!
Durée totale : environ 85 minutes
Sommaire
Dans cette situation d’apprentissage, les élèves explorent le concept de pourcentage dans le contexte d’un jeu d’adresse.
| Attente | Contenus d'apprentissage |
|
B1. Sens du nombre Démontrer sa compréhension des nombres et établir des liens avec leur utilisation dans la vie quotidienne. |
B1.3 Représenter des fractions équivalentes à partir des demis jusqu’aux douzièmes, y
compris des fractions impropres et des nombres fractionnaires, à l’aide d’outils appropriés, dans divers
contextes.
B1.7 Décrire les relations et représenter les équivalences entre des fractions, des nombres décimaux jusqu’aux centièmes et des pourcentages, à l’aide d’outils et de schémas appropriés, dans divers contextes. |
Intention pédagogique
Cette situation d’apprentissage a pour but d’amener les élèves :
- à comprendre le sens du pourcentage;
- à établir des liens entre les fractions, les nombres décimaux et les pourcentages;
- à convertir en pourcentage un nombre décimal ou une fraction dont le dénominateur est 100;
- à développer des stratégies de résolution de problèmes.
| Contexte pédagogique | Préalables |
|---|---|
| Au cours des années d’études précédentes, les élèves ont établi, dans divers contextes, des relations entre les nombres naturels, les fractions et les nombres décimaux. En 5e année, ils développent une compréhension du concept de pourcentage et établissent des liens entre les fractions, les nombres décimaux et les pourcentages. | La présente situation d’apprentissage permet aux élèves de développer un sens des pourcentages en
reconnaissant qu’il est possible de représenter une même quantité à l’aide d’un pourcentage, d’une fraction et
d’un nombre décimal. Pour être en mesure de réaliser cette situation d’apprentissage, les élèves doivent :
|
Matériel
- sacs de haricots secs
- récipient (par exemple, panier, poubelle, bac de recyclage)
- annexe 6.1 (Visez juste!) (1 copie par élève)
- annexe 6.2 (Lancers à une distance de 1 mètre) (1 copie par équipe)
- annexe 6.3 (Lancers à une distance de 2 mètres) (1 copie par équipe)
- annexe 6.4 (Lancers à une distance de 3 mètres) (1 copie par équipe)
- annexe 6.5 (Lancers à une distance de 4 mètres) (1 copie par équipe)
Vocabulaire mathématique
nombre décimal, fraction, fractions équivalentes, fraction décimale, centième et pourcentage
Avant l’apprentissage (mise en train)
Durée : environ 30 minutes
Au préalable, placer un récipient (par exemple, panier, poubelle, bac de recyclage) devant la classe et indiquer avec du ruban-cache les points situés à 1 mètre, à 2 mètres, à 3 mètres et à 4 mètres de ce récipient, comme illustré ci-dessous.
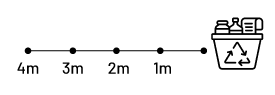
Expliquer aux élèves qu’elles et ils exploreront le concept de pourcentage à l’aide du jeu d’adresse Visez juste! Préciser que ce jeu consiste à tenter de lancer un sac de haricots secs dans un récipient à partir d’une distance donnée. Présenter le tableau ci-dessous (annexe 6.1) dans lequel le nombre de lancers réussis sera inscrit au fur et à mesure. Inviter :
- 5 élèves à effectuer chacune ou chacun 1 lancer à partir du point situé à 1 mètre du récipient;
- 10 élèves à effectuer chacune ou chacun 1 lancer à partir du point situé à 2 mètres du récipient;
- 20 élèves à effectuer chacune ou chacun 1 lancer à partir du point situé à 3 mètres du récipient;
- 25 élèves à effectuer chacune ou chacun 1 lancer à partir du point situé à 4 mètres du récipient.
Note : Le tableau ci-dessous propose un exemple de résultats possibles et toutes les explications subséquentes sont présentées en fonction de ces résultats. Toutefois, le personnel enseignant devrait en tout temps travailler avec des résultats obtenus par les élèves.
Exemple
| Distance du récipient | Nombre de lancers | Nombre de lancers réussis | Résultat en fraction | |||
|---|---|---|---|---|---|---|
| 1 m | 5 | 4 | ||||
| 2 m | 10 | 7 | ||||
| 3 m | 20 | 13 | ||||
| 4 m | 25 | 13 |
Distribuer, à chaque élève, une copie du tableau (annexe 6.1) afin qu’elles et ils puissent y transcrire les résultats obtenus. Remplir la 4e colonne, Résultat en fraction, avec eux.
Demander aux élèves de comparer les résultats obtenus en fonction de la distance à partir de laquelle les lancers sont effectués. Les amener à constater la difficulté que peut représenter la comparaison des résultats, puisque les dénominateurs diffèrent d’une situation à l’autre. Leur demander ensuite d’inscrire le titre Résultat en fraction (en centièmes) dans la 5e colonne et de déterminer pour chaque fraction de la 4e colonne, la fraction équivalente en centièmes.
Note : Pour déterminer une fraction équivalente en centièmes, les élèves pourraient utiliser un raisonnement proportionnel. Par exemple, 4 lancers réussis sur 5 lancers effectués c’est équivalent à 8 lancers réussis sur 10 lancers effectués (si on double le nombre de lancers effectués, on double le nombre de lancers réussis), à 12 lancers réussis sur 15 lancers effectués, et ainsi de suite. On peut poursuivre ce raisonnement jusqu’à 80 lancers réussis sur 100 lancers effectués (20 fois plus de lancers effectués donc 20 fois plus de lancers réussis).
Exemple
| Distance du récipient | Nombre de lancers | Nombre de lancers réussis | Résultat en fraction | Résultat en fraction (en centièmes) | ||
|---|---|---|---|---|---|---|
| 1 m | 5 | 4 | \(\frac{4}{5}\) | \(\frac{{80}}{{100}}\) | ||
| 2 m | 10 | 7 | \(\frac{7}{{10}}\) | \(\frac{{70}}{{100}}\) | ||
| 3 m | 20 | 13 | \(\frac{{13}}{{20}}\) | \(\frac{{65}}{{100}}\) | ||
| 4 m | 25 | 13 | \(\frac{{13}}{{25}}\) | \(\frac{{52}}{{100}}\) |
Ensuite, inviter les élèves à donner leurs réponses et à expliquer leurs stratégies. Poser des questions afin de comparer les fractions obtenues et les stratégies utilisées. Par exemple :
- Comment avez-vous obtenu les fractions en centièmes?
- Est-ce que d’autres élèves ont utilisé la même stratégie?
- Y en ont-elles et ils qui ont utilisé une stratégie différente?
- Quels sont les avantages d’écrire les résultats sur 100?
- Que signifie d’après vous le mot pourcentage?
- Dans quelles situations avez-vous déjà vu un pourcentage? (Par exemple, les taxes provinciale et fédérale imposées lors d’achats, des rabais sur des articles…)
Amener les élèves à comprendre que les résultats obtenus dans la 5e colonne, Résultat en fraction (en centièmes), peuvent aussi s’exprimer en pourcentage, ce mot signifiant tout simplement pour chaque cent. Souligner, par exemple, que la fraction \(\frac{{80}}{{100}}\) exprimée en pourcentage s’écrit 80 % et se lit « 80 pour cent ». Demander aux élèves d’inscrire le titre Résultat en pourcentage dans la 6e colonne ainsi que les résultats appropriés.
Exemple
| Distance du récipient | Nombre de lancers | Nombre de lancers réussis | Résultat en fraction | Résultat en fraction (en centièmes) | Résultat en pourcentage | |
|---|---|---|---|---|---|---|
| 1 m | 5 | 4 | \(\frac{4}{5}\) | \(\frac{{80}}{{100}}\) | 80 % | |
| 2 m | 10 | 7 | \(\frac{7}{{10}}\) | \(\frac{{70}}{{100}}\) | 70 % | |
| 3 m | 20 | 13 | \(\frac{{13}}{{20}}\) | \(\frac{{65}}{{100}}\) | 65 % | |
| 4 m | 25 | 13 | \(\frac{{13}}{{25}}\) | \(\frac{{52}}{{100}}\) | 52 % |
Amener les élèves à reconnaître que \(\frac{4}{5}\), \(\frac{{80}}{{100}}\) et 80 % représentent le même résultat, soit la réussite de 4 des 5 lancers. Donc, \(\frac{4}{5}\) = \(\frac{{80}}{{100}}\) = 80 %.
Note : Il importe de préciser le sens d’un pourcentage. Un résultat de réussite exprimé en pourcentage représente le nombre de lancers réussis par rapport à 100 essais. Par exemple, un résultat de 75 % signifie que si 100 lancers sont effectués, 75 lancers sont réussis. Cependant, insister sur le fait qu’un résultat donné en pourcentage n’implique pas qu’il y ait eu exactement 100 lancers. Toute situation qui peut être représentée par une fraction équivalente à \(\frac{{75}}{{100}}\) serait possible, par exemple, 15 lancers réussis sur 20 lancers effectués (\(\frac{{15}}{{20}}\)) ou 150 lancers réussis sur 200 lancers effectués (\(\frac{{150}}{{200}}\)).
Lire ensuite à haute voix les fractions exprimées en centièmes (5e colonne) et demander aux élèves si elles et ils connaissent une autre façon d’écrire ces nombres. Leur faire remarquer qu’elles et ils ont présenté les résultats des lancers en fraction et en pourcentage, mais qu’elles et ils auraient pu aussi le faire en nombre décimal, ces 3 notations différentes pouvant traduire le même résultat. Établir les relations entre un pourcentage, une fraction dont le dénominateur est 100 et le nombre décimal correspondant (par exemple, \(70\;\% \; = \;\frac{{70}}{{100}}\; = \;0,70\)).
Demander aux élèves d’inscrire le titre Résultat en nombre décimal dans la 7e colonne ainsi que les résultats appropriés.
Exemple
| Distance du récipient | Nombre de lancers | Nombre de lancers réussis | Résultat en fraction | Résultat en fraction (en centièmes) | Résultat en pourcentage | Résultat en nombre décimal |
|---|---|---|---|---|---|---|
| 1 m | 5 | 4 | \(\frac{4}{5}\) | \(\frac{{80}}{{100}}\) | 80 % | 0,80 |
| 2 m | 10 | 7 | \(\frac{7}{{10}}\) | \(\frac{{70}}{{100}}\) | 70 % | 0,70 |
| 3 m | 20 | 13 | \(\frac{{13}}{{20}}\) | \(\frac{{65}}{{100}}\) | 65 % | 0,65 |
| 4 m | 25 | 13 | \(\frac{{13}}{{25}}\) | \(\frac{{52}}{{100}}\) | 52 % | 0,52 |
Pendant l’apprentissage (Exploration)
Durée : environ 35 minutes
Présenter la suite de la situation d’apprentissage.
Pour rendre le jeu d’adresse plus intéressant, nous allons imposer les contraintes suivantes :
- certains des lancers effectués à une distance de 1 mètre du récipient seront faits de dos, par-dessus l’épaule;
- certains des lancers effectués à une distance de 2 mètres du récipient seront faits avec la main gauche pour les droitiers et avec la main droite pour les gauchers;
- certains des lancers effectués à une distance de 3 mètres du récipient seront faits en se tenant debout sur une jambe;
- certains des lancers effectués à une distance de 4 mètres du récipient seront faits en fermant un œil.
Avant d’exécuter les lancers, vous devez effectuer quelques calculs.
Grouper les élèves par 2. Distribuer une copie des annexes 6.2, 6.3, 6.4 et 6.5 à chaque équipe. Leur expliquer la tâche à réaliser à l’aide de l’annexe 6.2
Expliquer que parmi les 5 lancers effectués à une distance de 1 mètre du récipient, 60 % doivent être faits de dos, par-dessus l’épaule. Leur préciser qu’elles et ils doivent :
- déterminer le nombre de lancers à effectuer selon la contrainte;
- estimer le pourcentage de lancers qui seront réussis, selon une stratégie d’estimation de leur choix.
Demander aux élèves d’accomplir le travail demandé (annexes 6.2, 6.3, 6.4 et 6.5) en s’assurant de tenir compte de la contrainte dans chaque situation. Préciser que les élèves doivent garder des traces de leur travail pour pouvoir partager leur raisonnement au cours de l’échange mathématique.
Exemple
| Distance du récipient | Nombre de lancers à effectuer | Pourcentages des lancers à effectuer en suivant la contrainte | Nombre décimal représentant les lancers à effectuer en suivant la contrainte | Fraction des lancers à effectuer en suivant la contrainte | Nombre de lancers à effectuer en suivant la contrainte | Estimation du pourcentage de réussite |
|---|---|---|---|---|---|---|
| 1 m | 5 | 60 % | 0,60 | \(\frac{{60}}{{100}}\) | 3 | 70 % |
Montrez comment vous avez obtenu vos résultats.

Justifiez l’estimation du pourcentage de réussite à l’aide d’explications, de dessins ou de calculs.
Le pourcentage de lancers réussis pour les lancers effectués à une distance de 1 mètre lors de la mise en train était de 80 %. Avec la contrainte, il devrait être inférieur. J’estime donc que le pourcentage de réussite sera d’environ 70 %.
Note : Vous devez pouvoir exposer votre raisonnement à la classe au cours de l’échange mathématique.
| Observations possibles | Interventions possibles |
|---|---|
| Une équipe ne sait pas comment convertir 60 % en fraction. | Poser des questions telles que :
Établir le lien entre le pourcentage et la fraction correspondante, soit 60 %, 60 pour cent, \(\frac{{60}}{{100}}\). |
| Une équipe ne peut déterminer combien des 5 lancers doivent être effectués de dos, par-dessus l’épaule. | Modéliser un raisonnement proportionnel. Expliquer par exemple, pourquoi la situation où 60 lancers sur 100
doivent être effectués de dos, par-dessus l’épaule, équivaut à celle où 30 lancers sur 50 doivent l’être (les
2 quantités sont divisées par 2). Leur demander ensuite :
|
| Une équipe ne comprend pas ce qui doit être fait dans la dernière colonne. | Leur rappeler que lors de la mise en train, 4 des 5 lancers effectués à une distance de 1 mètre avaient été réussis, ce qui correspondait en pourcentage à 80 %. Leur dire qu’elles et ils doivent maintenant estimer le pourcentage probable de réussite de ces lancers en tenant compte de la contrainte. |
| Une équipe ne sait pas comment convertir \(\frac{1}{5}\) en pourcentage. | Demander aux élèves de trouver des fractions équivalentes à \(\frac{1}{5}\) (par exemple, \(\frac{2}{{10}}\), \(\frac{4}{{20}}\)). Leur demander ensuite ce que représente un pourcentage afin de faire ressortir que celui-ci peut être représenté par une fraction ayant un dénominateur de 100. |
Après l’apprentissage (objectivation/transfert de connaissances)
Durée : environ 20 minutes
Demander à quelques équipes de présenter la stratégie utilisée pour traiter les lancers effectués à une distance de 1 mètre et de justifier leur estimation.
Note : Lors de l’échange mathématique, le choix des équipes est très important, puisque c’est par l’entremise des présentations que les élèves pourront comparer leurs stratégies de conversion entre un pourcentage, un nombre décimal et une fraction à celles des autres élèves et objectiver leur apprentissage.
Après chaque présentation, inciter les autres élèves à enrichir l’échange mathématique en posant des questions et en faisant des observations pertinentes. Au besoin, les aider en posant des questions telles que :
- Est-ce une stratégie efficace? Pourquoi?
- Pouvez-vous expliquer dans vos mots la stratégie qui vient d’être présentée?
- Est-ce que d’autres élèves ont utilisé cette stratégie?
- De quelle autre façon ces résultats auraient-ils pu être trouvés?
- Cette estimation est-elle raisonnable? Pourquoi?
- Est-ce que quelqu’un a obtenu la même estimation, mais en utilisant un raisonnement différent?
- Est-ce que d’autres ont des estimations différentes?
Par la suite, inviter 5 élèves à venir exécuter chacun et chacune un lancer à partir du point situé à 1 mètre du récipient en respectant la nouvelle consigne : 3 élèves effectuent un lancer en suivant la contrainte et 2, sans la suivre. Déterminer le pourcentage de réussite et le comparer aux pourcentages de réussite estimés par les élèves.
Reprendre la même démarche pour les 3 autres séries de lancers (annexes 6.3, 6.4 et 6.5).
Note : Mettre l’accent sur le sens d’un pourcentage et faire ressortir diverses stratégies de conversion :
- conversion d’une fraction en nombre décimal (par exemple, \(\frac{2}{5}\; = \;\frac{4}{{10}}\; = \;0,4\) ou \(2\; \div \;5\; = \;0,4\));
- conversion d’un nombre décimal en fraction décimale (par exemple, \(0,45\; = \;\frac{{45}}{{100}}\); \(0,7\; = \;\frac{7}{{10}}\));
- conversion d’une fraction en pourcentage (par exemple, \(\frac{3}{5}\; = \;\frac{6}{{10}}\; = \;\frac{60}{100}\; = \;60\;\% \) ou \(3\; \div \;5\; = \;0,60\; = \;60\;\% \));
- conversion d’un pourcentage en fraction décimale (par exemple, \(5\;\% \; = \;\frac{5}{{100}}\); \(77\;\% \; = \;\frac{{77}}{{100}}\)).
Différenciation pédagogique
L’activité peut être modifiée pour répondre aux différents besoins des élèves.
| Pour faciliter la tâche | Pour enrichir la tâche |
|---|---|
| Fournir à l’équipe le nombre de lancers au lieu du pourcentage et se concentrer sur les stratégies de
conversion.
Exemple Pour les lancers effectués à une distance de 1 mètre du récipient, écrire que 3 des 5 lancers doivent être effectués de dos, par-dessus l’épaule, et demander aux élèves de déterminer le pourcentage que cela représente. |
Demander aux élèves d’accorder des points à chaque lancer réussi du jeu Visez juste! en fonction de la
distance à partir de laquelle il est effectué. L’objectif est d’obtenir, pour chacune des distances, un
score d’environ 200 points après 10 lancers.
Exemple Une ou un élève pourrait suggérer d’accorder 28 points à chaque lancer réussi effectué à une distance de 2 mètres du récipient en expliquant que lors de la mise en train, 70 % des lancers ont été réussis, soit 7 lancers sur 10 et que \(7\; \times \;28\) points = 196 points. Elle ou il ferait de même pour les 3 autres distances. |
Suivi à la maison
Suggérer aux élèves d’inventer un jeu d’adresse (par exemple, renverser une quille en faisant rouler une balle) et d’inviter des membres de la famille à y participer. Préciser le nombre d’essais à effectuer (5, 10, 20, 25 ou 50 essais) afin d’obtenir des fractions qui peuvent être facilement converties en pourcentages. Leur demander de compiler les résultats dans un tableau semblable à celui utilisé lors de la mise en train.
Le lendemain, leur proposer de présenter leur jeu et d’inviter leurs camarades à jouer. Une fois un tableau de données rempli, leur demander de comparer les résultats en pourcentage avec ceux obtenus à la maison.
Source: Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 165-175.
Situation d’apprentissage 2 : le pique-nique des fractions
Durée totale : 1 h 40 min
Sommaire
Dans cette situation d’apprentissage, les élèves utilisent des nombres fractionnaires et des fractions impropres pour comparer des quantités de sandwichs.
| Attente | Contenus d'apprentissage |
|
B1. Sens du nombre Démontrer sa compréhension des nombres et établir des liens avec leur utilisation dans la vie quotidienne. |
B1.3 Représenter des fractions équivalentes à partir des demis jusqu’aux douzièmes, y
compris des fractions impropres et des nombres fractionnaires, à l’aide d’outils appropriés, dans divers
contextes.
B1.4 Comparer et ordonner des fractions à partir des demis jusqu’aux douzièmes, y compris des fractions impropres et des nombres fractionnaires, dans divers contextes. |
Intention pédagogique
Cette situation d’apprentissage a pour but d’amener les élèves :
- à développer le sens de la quantité représentée à l’aide de fractions impropres et de nombres fractionnaires;
- à reconnaître le lien entre diverses représentations équivalentes d’une même quantité (fraction impropre, nombre fractionnaire, fractions équivalentes, représentation symbolique, représentation semi-concrète, fraction en tant que division et fraction en tant que partie d’un tout);
- à développer des stratégies de résolution de problèmes.
| Contexte pédagogique | Préalables |
|---|---|
| Au cours des années précédentes, les élèves ont acquis une compréhension du concept de fraction par l’exploration de fractions qui représentent une quantité inférieure à un tout, c’est-à-dire les fractions propres (par exemple, \(\frac{5}{8}\)). En 5e année, elles et ils approfondissent leur compréhension de ce concept en explorant les fractions qui représentent une quantité supérieure à l’entier, soit les fractions impropres (par exemple, \(\frac{5}{3}\)) ou les nombres fractionnaires (par exemple, \(1\frac{1}{3}\)). Elles et ils étudient également le concept de fractions équivalentes. | La présente situation d’apprentissage permet, dans un contexte de résolution de problèmes, de développer le
sens de la quantité représentée par un nombre fractionnaire et par une fraction impropre. Elle favorise aussi
la création de liens entre les fractions propres, les fractions impropres, les nombres fractionnaires et les
nombres naturels ainsi qu’entre leurs représentations (symbolique, semi-concrète, concrète).
Pour être en mesure de réaliser cette situation d’apprentissage, les élèves doivent :
|
Vocabulaire mathématique
fraction, numérateur, dénominateur, partie d’un tout, division, fraction propre, fraction impropre, nombre fractionnaire, entier, fractions équivalentes
Matériel
- annexe 5.1A (Pique-nique scolaire – partie 1) (1 copie par équipe)
- annexe 5.1B (Pique-nique scolaire – partie 2) (1 copie par équipe)
- annexe 5.2A et annexe 5.2B (Solutions)
- annexe 5.3 (Explications d’élèves)
- marqueurs
- grandes feuilles de papier (1 par équipe)
- tableau interactif
Avant l’apprentissage (mise en train)
Durée : 15 minutes
Cette mise en train a pour but de permettre aux élèves de reconnaître la représentation d’une quantité à l’aide d’un nombre fractionnaire et d’une fraction impropre. Présenter la situation suivante, en complétant un tableau comme celui ci-après :
Lors d’un pique-nique de classe, il y avait au menu des petites pizzas coupées en 4 morceaux égaux. Un élève a mangé un morceau de pizza. Quelle quantité de pizza a-t-il mangée? (\(\frac{1}{4}\) de pizza)
Il a ensuite mangé un 2e morceau. Quelle quantité de pizza a-t-il mangée en tout? (2 fois \(\frac{1}{4}\) de pizza ou \(\frac{2}{4}\) de pizza; les élèves mentionneront probablement \(\frac{1}{2}\))
Puis, il en a mangé un 3e. Quelle quantité de pizza a-t-il mangée en tout? (3 fois \(\frac{1}{4}\) de pizza ou \(\frac{3}{4}\) de pizza)
Puis, un 4e. Quelle quantité de pizza a-t-il mangée en tout? (4 fois \(\frac{1}{4}\) de pizza, \(\frac{4}{4}\) de pizza ou 1 pizza)
Et finalement, un 5e. Quelle quantité de pizza a-t-il mangée en tout? (5 fois \(\frac{1}{4}\) de pizza, \(\frac{5}{4}\) de pizza ou \(1\frac{1}{4}\) de pizza)

Un morceau, c’est un sur 4, soit un quart de pizza, c’est une fraction propre.
Deux morceaux, c’est 2 sur 4, soit 2 quarts, c’est une fraction propre.
Trois morceaux, c’est 3 sur 4, soit 3 quarts, c’est une fraction propre.
Quatre morceaux, c’est 4 sur 4, soit 4 quarts ou une pizza, c’est une fraction unité ou un nombre entier.
Cinq morceaux, c’est 5 sur 4, soit 5 quarts, c’est une fraction impropre. On peut aussi dire que c’est un et un sur 4, soit un et un quart, c’est un nombre fractionnaire.
Faire remarquer que dans les fractions \(\frac{1}{4}\), \(\frac{2}{4}\) et \(\frac{3}{4}\) le numérateur est inférieur au dénominateur et souligner que ces fractions sont appelées des fractions propres. Noter qu’il n’est pas essentiel que le numérateur d’une fraction soit inférieur au dénominateur. Mentionner qu’une fraction dont le numérateur est supérieur au dénominateur est une fraction impropre et qu’elle représente alors une quantité supérieure à un tout. Par exemple, dans la présente situation lorsque l’élève a mangé 5 morceaux de pizza en tout, on a écrit \(\frac{5}{4}\) de pizza. La fraction \(\frac{5}{4}\) se lit « 5 quarts » et signifie \(\frac{1}{4}\; + \;\frac{1}{4}\; + \;\frac{1}{4}\; + \;\frac{1}{4}\; + \;\frac{1}{4}\; = \;5\; \times \;\frac{1}{4}\; = \;\frac{5}{4}\). De la même façon que \(\frac{2}{4}\) signifie 2 morceaux de touts séparés en quarts, \(\frac{5}{4}\) signifie 5 morceaux de touts séparés en quarts.
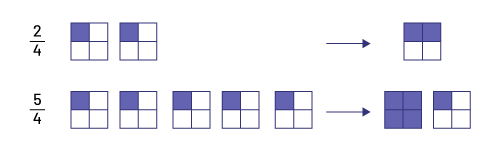 Image
Des carrés divisés en 4 parties égales représentent des fractions. 2 sur 4, 2 carrés dont chacun a une case
ombragée. On peut aussi le représenter avec un carré avec 2 cases ombragées. 5 sur 4, 5 carrés dont chacun a une
case ombragée. On peut aussi le représenter avec 2 carrés, l’un a 4 cases ombragées et l’autre une case.
Image
Des carrés divisés en 4 parties égales représentent des fractions. 2 sur 4, 2 carrés dont chacun a une case
ombragée. On peut aussi le représenter avec un carré avec 2 cases ombragées. 5 sur 4, 5 carrés dont chacun a une
case ombragée. On peut aussi le représenter avec 2 carrés, l’un a 4 cases ombragées et l’autre une case.
Note : Lorsque le numérateur d’une fraction est égal à son dénominateur (par exemple, \(\frac{3}{3}\) et \(\frac{8}{8}\)), l’expression fraction-unité est utilisée. Toutefois, il ne s’agit pas d’un terme que les élèves doivent maîtriser.
Expliquer qu’on peut aussi représenter une quantité supérieure au tout à l’aide d’un nombre fractionnaire. Préciser que \(1\frac{1}{4}\) se lit « 1 et 1 quart », que le chiffre 1 représente le nombre de touts et que la fraction \(\frac{1}{4}\) représente la partie fractionnaire d’un tout équivalent. Dans cette situation, l’élève a donc mangé, au total, une pizza entière (\(\frac{4}{4}\) de pizza) et \(\frac{1}{4}\) d’une autre de la même taille.
Spécifier que la fraction impropre \(\frac{5}{4}\) et le nombre fractionnaire \(1\frac{1}{4}\) sont 2 façons de représenter une même quantité. À ce stade, il est important de simplement présenter les types de nombres sans insister sur leurs liens puisque les élèves les exploreront un peu plus loin dans cette situation d’apprentissage.
Faire un bref retour sur le concept de fractions équivalentes en précisant qu’il s’agit aussi de façons différentes de représenter une même quantité. Par exemple, mentionner que \(\frac{2}{4}\) de sandwich est l’équivalent de \(\frac{1}{2}\) de sandwich, que \(\frac{1}{3}\) de sandwich est l’équivalent de \(\frac{2}{6}\) ou de \(\frac{4}{{12}}\) de sandwich et démontrer comment on peut confirmer qu’elles représentent bien une quantité équivalente.
Présenter l’annexe 5.1A, lire la mise en situation et expliquer la tâche à effectuer, soit d’établir, à l’aide de fractions impropres et de nombres fractionnaires, la quantité qu’a reçue chaque membre de chaque groupe afin de déterminer si la répartition des sandwichs était équitable.
S’assurer que les élèves ont bien compris la tâche en posant des questions telles que :
- Qui peut expliquer la situation? Qu’est-il arrivé lors de ce pique-nique?
- Pourquoi pense-t-on que chaque élève n’a pas reçu la même quantité?
- Qui peut expliquer dans ses propres mots la tâche à effectuer?
- Qu’est-ce qu’un nombre fractionnaire?
- Qu’est-ce qu’une fraction impropre?
Pendant l’apprentissage (exploration)
Durée : 55 minutes
Grouper les élèves par 2 et leur distribuer une copie de l’annexe 5.1A. Leur demander d’accomplir la tâche en utilisant les stratégies de leur choix.
Allouer suffisamment de temps pour permettre aux élèves de discuter du problème et de le résoudre. Circuler et observer les stratégies utilisées. Intervenir au besoin afin d’aider certaines équipes à cheminer, sans toutefois leur montrer comment transformer en fraction impropre une quantité exprimée par un nombre fractionnaire et inversement.
Inviter les élèves à laisser des traces de leur raisonnement et à inscrire près de leurs calculs et de leurs illustrations, le numéro de l’énoncé correspondant. L’annexe 5.2A présente des éléments de solution.
Généralement, afin d’accomplir la tâche, les élèves illustrent d’abord chaque énoncé de manière à représenter la quantité correspondante. Cette quantité est ensuite exprimée symboliquement par une fraction impropre, puis par un nombre fractionnaire. Leur stratégie se raffine au fur et à mesure qu’elles et ils cheminent dans la situation d’apprentissage et qu’elles et ils développent le sens de quantité représentée par la fraction impropre et par le nombre fractionnaire. Puisque la comparaison de quantités est reliée à l’équivalence, elles et ils doivent aussi reconnaître que certains énoncés mènent à l’utilisation de fractions équivalentes (par exemple, \(1\frac{4}{6}\; = \;1\frac{2}{3}\)).
| Observations possibles | Interventions possibles |
| Après la lecture de l’énoncé 2, une équipe tente de déterminer le nombre de personnes qu’il y a dans le groupe au lieu de chercher la quantité de sandwichs reçue. | Poser des questions telles que :
Que devez-vous déterminer? Pour cela, est-il nécessaire de connaître le nombre de personnes qui constituent le groupe? |
| Une équipe ne peut pas comparer les situations équivalentes puisqu’elle ne remarque pas que \(\frac{4}{6}\; = \;\frac{2}{3}\). | Poser des questions telles que :
|
Une équipe représente l’énoncé 1 comme la fraction d’un tout, alors que la situation correspond davantage à
la fraction d’un ensemble. De plus, elle ignore comment diviser les 4 sandwichs qui restent.
|
Poser des questions telles que :
|
Lorsque les élèves ont presque terminé la 1re partie du travail, distribuer à chaque équipe l’annexe 5.1B. Préciser que la 1re partie leur a permis d’explorer les nombres fractionnaires et les fractions impropres et que cette 2e partie leur permettra d’approfondir leur compréhension de ces concepts.
Suggérer aux élèves d’examiner leurs représentations illustrées dans la 1re partie pour déterminer des calculs possibles afin de résoudre les problèmes plutôt que d’illustrer l’énoncé. Ajouter qu’elles et ils peuvent avoir recours à l’illustration si nécessaire.
Note : Il s’agit de leur permettre de cheminer de la représentation semi-concrète vers le raisonnement qui sous-tend l’opération mathématique. Toutefois, il ne s’agit pas de présenter l’algorithme ou les étapes à suivre, mais bien d’amener les élèves à établir un lien entre le sens du problème, les nombres en cause et le raisonnement qu’ils impliquent. En ce sens, l’annexe 5.2B présente des éléments de solution.
Circuler, observer et choisir les équipes qui présenteront lors de l’échange mathématique. Les cibler en fonction des forces et des faiblesses de leurs stratégies.
Une fois les tâches complétées, assigner 1 ou 2 problèmes de la situation d’apprentissage par équipe, leur distribuer de grandes feuilles et des marqueurs et leur allouer suffisamment de temps pour se préparer afin de participer pleinement à l’échange mathématique. Préciser qu’elles et ils doivent présenter les raisonnements ou les stratégies utilisées pour résoudre le problème assigné.
Après l’apprentissage (objectivation/transfert de connaissances)
Durée : 30 minutes
Inviter les équipes choisies à présenter leur démarche. S’assurer que chacune identifie la question ou l’énoncé présenté en mentionnant son numéro, en lisant le texte ou en le transcrivant au tableau. Inviter les élèves à intervenir et à ajouter des commentaires.
Animer l’échange en posant des questions.
Par exemple
- Qui peut expliquer la démarche de cette équipe?
- Est-ce que d’autres équipes ont utilisé cette stratégie ou une stratégie similaire?
- Ces 2 équipes expriment des réponses différentes pour le même problème. Comment est-ce possible? (Faire ressortir l’équivalence des diverses représentations : les fractions équivalentes ainsi que l’équivalence entre le nombre fractionnaire et la fraction impropre.)
- Pour résoudre le problème de l’énoncé 1, pourquoi ont-elles ou ils divisé par 6?
- Comment avez-vous procédé pour trouver la quantité du groupe d’Abdul même si on ne mentionnait pas le nombre de personnes qui le constituait?
- Qu’entendent-ils par « nous avons fait la division », alors qu’on parle de fraction?
- Pourquoi dites-vous que \(1\frac{4}{6}\) est équivalent à \(1\frac{2}{3}\)?
- Certains groupes parlent surtout de sixièmes alors que d’autres réfèrent à des tiers. Quelle est la différence?
- Afin de résoudre le problème de cantaloups, pourquoi parlez-vous de multiplication, de division et de reste?
- Quelle est la différence entre l’énoncé d’Amon (« Chaque membre du groupe a reçu 5 tiers de sandwich. ») et celui d’Abdul (« C’était délicieux. Il y avait 8 sandwichs pour Jean, Pierre et moi. »)? [Souligner que le 1er énoncé présente la fraction comme partie d’un tout (\(\frac{5}{3}\) de sandwich) alors que le 2e présente une situation de partage (8 sandwichs pour 3 personnes : donc 8 ÷ 3 peut être représenté par \(\frac{8}{3}\)).]
Encourager les élèves à utiliser des arguments clairs, un vocabulaire précis et des termes de causalité. L’annexe 5.3 fournit des exemples de raisonnements d’élèves, d’arguments mathématiques et de stratégies de résolution.
Faire ressortir des stratégies efficaces de conversion d’une fraction impropre en un nombre fractionnaire et inversement, en établissant des liens entre les représentations semi-concrètes et la signification des nombres qui les composent (les touts, la partie fractionnaire, la division, le reste). Il est plus important pour les élèves de comprendre le sens des nombres et des opérations effectuées que de mémoriser les étapes à suivre.
Différenciation pédagogique
L’activité peut être modifiée pour répondre aux différents besoins des élèves.
| Pour faciliter la tâche | Pour enrichir la tâche |
|
|
Suivi à la maison
À la maison, les élèves peuvent utiliser des représentations concrètes et semi-concrètes pour résoudre 1 ou 2 problèmes reliés aux nombres fractionnaires et aux fractions impropres.
Exemples de problèmes
- Si le rectangle ci-dessous correspond aux \(\frac{5}{4}\) d’un tout, dessine le tout.

- Pour s’entraîner, Pierre parcourt à plusieurs reprises le quart du trajet prévu pour une course à bicyclette. Il parcourt à 7 reprises le quart du trajet. L’odomètre installé sur sa bicyclette indique qu’il a parcouru 14 km au total. Quelle est la longueur du trajet de la course?

- Sachant que sur \(1\frac{2}{3}\) feuille de gommettes il y a 35 gommettes, combien y a-t-il de gommettes sur 1 feuille?
- J’ai 3 petites bandes de papier de même longueur. Lorsque je place bout à bout 2 bandes entières et \(\frac{2}{3}\) de la 3e, j’obtiens une grande bande de papier mesurant 240 cm. Quelle est la longueur d’une des petites bandes?

- Après la fête, il reste 2 gâteaux rectangulaires entiers et une partie d’un 3e. Quelle quantité de gâteaux reste-t-il?

Source: Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 147-157.
Situation d’apprentissage 3 : la salle de théâtre
Durée totale : 85 minutes
Sommaire
Dans cette situation d’apprentissage, les élèves utilisent diverses stratégies pour estimer le nombre de spectateurs qu’une salle de spectacle peut contenir. Elles et ils déterminent ensuite de façon approximative le profit ou le déficit généré par un spectacle présenté à guichets fermés.
| Attente | Contenus d'apprentissage |
|
B1. Sens du nombre Démontrer sa compréhension des nombres et établir des liens avec leur utilisation dans la vie quotidienne. |
B1.1 Lire, représenter, composer et décomposer les nombres naturels de 0 jusqu’à 100 000,
à l’aide d’outils et de stratégies appropriés, et décrire de quelles façons ils sont utilisés dans la vie
quotidienne.
B1.2 Comparer et ordonner les nombres naturels jusqu’à 100 000, dans divers contextes. Note : Cette situation touche aussi l’attente B2 (sens des opérations). |
Intention pédagogique
Cette situation d’apprentissage a pour but d’amener les élèves à :
- développer le sens des grands nombres dans un contexte réel;
- appliquer des stratégies d’estimation et de calcul;
- vérifier la vraisemblance du résultat d’un calcul;
- établir un lien entre l’arrondissement et l’estimation.
| Contexte pédagogique | Préalables |
|---|---|
| Au cours des années d’études précédentes, les élèves ont appris à comparer, à ordonner et à représenter les nombres naturels jusqu’à 10 000. Elles et ils ont estimé le résultat de diverses opérations arithmétiques, notamment des opérations comprenant des montants d’argent. En 5e année, elles et ils développent davantage ces habiletés dans le but d’acquérir une compréhension de la quantité représentée par de plus grands nombres naturels (jusqu’à 100 000). | La présente situation d’apprentissage permet aux élèves d’approfondir leur habileté à estimer en appliquant
diverses stratégies appropriées.
Pour être en mesure de réaliser cette situation d’apprentissage, les élèves doivent :
|
Vocabulaire mathématique
estimation, arrondissement, plus que, moins que, environ, entre, approximation
Matériel
- annexe 5.1 (Salle de théâtre) (1 copie par équipe)
- annexe 5.2 (Plan de la salle) (1 copie par équipe)
- annexe 5.2 (Plan de la salle) en grand format (1 copie par équipe)
- grandes feuilles de papier (1 par équipe)
- crayons-feutres
- bâtonnets de colle
Avant l’apprentissage (mise en train)
Durée : environ 15 minutes
Demander aux élèves si elles et ils ont déjà assisté à un spectacle, à une pièce de théâtre, à un concert ou pris part à un grand rassemblement et, le cas échéant, si elles et ils se souviennent du nombre approximatif de spectateurs. Discuter avec elles et eux afin de vérifier si elles et ils ont simplement deviné ce nombre ou si elles et ils ont utilisé une stratégie d’estimation.
Faire un retour sur les mots estimation, arrondissement, plus que, moins que, environ, entre, approximation.
Présenter la mise en situation suivante aux élèves :
Une troupe de théâtre aimerait louer une grande salle pour présenter sa nouvelle pièce. La direction de la troupe doit déterminer le coût des billets. Après discussion, les membres de la troupe lui suggèrent de fixer le prix à 19,75 $ le billet.
Présenter l’annexe 5.2 au tableau interactif juste assez longtemps pour que les élèves puissent avoir une idée de la grandeur de la salle, sans toutefois leur laisser le temps de compter, par exemple, le nombre de sièges par rangée.
Leur demander d’inscrire sur un bout de papier, le nombre de sièges qu’ils pensent que la salle contient. Plus tard, lors de l’échange mathématique, ils pourront comparer ce nombre avec un nombre qu’ils auront obtenu en utilisant une stratégie d’estimation. Cette comparaison devrait leur permettre de constater à nouveau l’avantage de connaître et d’utiliser de telles stratégies, notamment lorsqu’il est question de grands nombres.
Note : Le nombre de sièges de la salle n’est pas précisé, car il est important, dans cette situation de ne pas prêter une attention particulière au nombre exact afin de miser davantage sur les stratégies et le concept d’estimation.
Montrer l’annexe 5.1 au tableau interactif ou sur une grande feuille, présenter le problème suivant aux élèves.
La troupe de théâtre souhaite louer la salle que je viens de vous montrer pour présenter sa pièce. Elle prévoit un budget de 22 230 $ pour l’ensemble des dépenses reliées à cette présentation (par exemple, location de la salle, éclairage, son, programme). Si la direction de la troupe retient la suggestion de fixer le prix d’un billet à 19,75 $ et si tous les billets sont vendus, est-ce que la troupe fera un profit? Si oui, quel sera-t-il environ? Sinon, quel sera le déficit?
S’assurer que les élèves comprennent bien le problème en leur demandant d’expliquer dans leurs propres mots la situation, ainsi que les termes profit et déficit.
Note : Il est important de ne pas fournir trop de pistes aux élèves; il faut les laisser trouver des stratégies personnelles de résolution de problèmes et d’estimation.
Pendant l’apprentissage (exploration)
Durée : environ 40 minutes
Grouper les élèves par 2.
Distribuer une copie de l’annexe 5.1 et de l’annexe 5.2 à chaque équipe. Leur demander de résoudre le problème en laissant des traces de leur démarche; préciser qu’elles et ils peuvent écrire sur le plan. Afin d’encourager les élèves à arrondir, ne pas permettre l’usage de la calculatrice pendant l’exploration.
Observer les élèves et les appuyer dans leur travail, sans toutefois leur dire comment relever le défi.
Il faut les amener, par des interventions stratégiques, à réfléchir :
- aux stratégies à utiliser pour résoudre le problème;
- à la nature approximative de la quantité recherchée.
Allouer suffisamment de temps pour permettre aux élèves d’explorer diverses stratégies de résolution de problèmes et d’en discuter.
Circuler et intervenir au besoin en posant des questions telles que :
- Comment pouvez-vous représenter cette situation autrement? Pouvez-vous résoudre le problème à l’aide d’une autre représentation?
- Cette quantité est-elle vraisemblable?
Les élèves choisiront diverses stratégies afin de résoudre le problème. Voici quelques exemples de stratégies qu’elles et ils pourraient utiliser pour estimer le nombre total de sièges :
- utiliser la symétrie (par exemple, estimer la quantité de sièges que contient la moitié de la salle, puis doubler ce nombre);
- délimiter des sections qui forment une disposition rectangulaire et estimer le nombre de sièges que chacune contient;
- compter, pour chacune des sections, le nombre moyen de sièges que contient une rangée ainsi que le nombre de rangées et déterminer le produit de ces nombres;
- arrondir les quantités pour simplifier les calculs;
- établir une correspondance entre une mesure linéaire sur le plan et le nombre de sièges (par exemple, 1 cm correspond à 5 sièges).

Note : Lorsqu’elles et ils effectuent des calculs pour déterminer s’il y a profit ou non, les élèves manipulent de grands nombres; il est par conséquent important de favoriser l’utilisation d’algorithmes personnels. Rappeler l’importance de vérifier si la réponse est vraisemblable.
| Observations possibles | Interventions possibles |
| Une équipe ne sait pas quoi faire avec les nombres qui figurent dans les cases sur le plan de la salle. | Poser des questions telles que :
|
| Une équipe tente de dénombrer les sièges 1 par 1. | Poser des questions telles que :
|
| Une équipe a de la difficulté à effectuer des calculs à l’aide des algorithmes usuels. | Poser des questions telles que :
|
| Une équipe a estimé le nombre de sièges à 2 355 et obtenu une réponse à la suite d’un calcul qui n’est pas vraisemblable (par exemple, \(19,75\;\$ \; \times \;2\;355\; = \;90\;636\;\$ \)). | Poser des questions telles que :
|
Afin que les élèves se préparent à l’échange mathématique, distribuer aux équipes une grande feuille ainsi que le plan agrandi de la salle. Leur demander de coller ce plan au milieu de la grande feuille et d’y noter leurs calculs. Leur rappeler qu’elles et ils doivent se préparer à expliquer les stratégies d’estimation utilisées et à justifier leur choix à l’aide d’arguments mathématiques clairs et convaincants.
Choisir les équipes qui présenteront lors de l’échange mathématique. Cibler celles qui ont utilisé différentes stratégies d’estimation et de calcul (par exemple 2 équipes qui sont parvenues à une estimation similaire du nombre de sièges dans la salle en utilisant respectivement la symétrie et la disposition rectangulaire). Il peut aussi être utile de choisir une équipe dont la stratégie n’a pas conduit aux résultats escomptés dans la mesure où l’accent est mis sur une analyse constructive des raisons qui font que cette stratégie était moins appropriée à la situation donnée.
Après l’apprentissage (objectivation/transfert de connaissances)
Durée : environ 30 minutes
Dans un premier temps, demander à certaines des équipes sélectionnées de présenter à tour de rôle la stratégie utilisée pour estimer le nombre de sièges que la salle peut contenir. Inciter les élèves à fournir des justifications précises en utilisant des arguments mathématiques clairs et convaincants. Par exemple : « Puisque les 3 sections du haut, sans les loges, contiennent à peu près le même nombre de sièges, nous avons estimé le nombre de sièges dans une section et l’avons multiplié par 3. »
Lors des discussions, il est important de faire ressortir les différentes stratégies d’estimation utilisées et de les comparer en posant des questions telles que :
- Pourquoi votre stratégie d’estimation fonctionne-t-elle?
- Est-ce que cette stratégie fonctionnerait avec le plan d’une autre salle?
- Est-ce que d’autres équipes ont utilisé cette stratégie?
- Quelles autres stratégies permettraient d’obtenir des résultats semblables?
- Selon vous, quelle stratégie est la plus efficace? Pourquoi?
- Y a-t-il de grandes différences entre les estimations du nombre de sièges obtenus par les différentes équipes? (Faire ressortir que malgré la diversité des stratégies utilisées, plusieurs équipes ont obtenu des estimations très semblables et aussi valables les unes que les autres.)
Demander ensuite aux membres des équipes sélectionnées de révéler le nombre de sièges qu’elles et ils ont noté sur un bout de papier lorsqu’elles et ils ont vu le plan pour la première fois. Afin d’inciter tous les élèves à réfléchir à la différence entre la vraisemblance d’une quantité obtenue en devinant et la vraisemblance d’une quantité obtenue en estimant, poser des questions telles que :
- Lorsque vous avez vu le plan pour la 1re fois, quel nombre avez-vous écrit sur votre bout de papier? Ce nombre était-il une estimation? (Ce n’était pas une estimation, car le temps alloué ne permettait pas d’utiliser une stratégie d’estimation appropriée.)
- Une quantité obtenue en estimant est-elle plus vraisemblable qu’une quantité obtenue en devinant? Pourquoi? (Oui, une quantité obtenue en estimant est généralement plus vraisemblable parce qu’elle n’est pas le fruit du hasard; elle est fondée sur un calcul rapide, mais réfléchi.)
Dans un deuxième temps, demander aux autres équipes sélectionnées de présenter les calculs qu’elles ont effectués pour déterminer si la troupe fera un profit ou un déficit. Mettre l’accent sur les différentes stratégies de calcul utilisées ainsi que sur la vérification de la vraisemblance des réponses. Faire ressortir l’importance d’arrondir les nombres pour faciliter les calculs.
Poser des questions telles que :
- Comment avez-vous déterminé si la troupe fera un profit ou un déficit?
- Pourquoi les équipes ont-elles obtenu des réponses différentes? Est-ce acceptable?
- Comment savez-vous que votre réponse est vraisemblable?
- La troupe fera-t-elle vraisemblablement plus ou moins de profit (ou de déficit) que le montant que vous avez déterminé?
- Qu’est-ce qui justifie l’utilisation d’arrondissements?
Tout au long de l’échange, inviter les autres élèves à réagir à chacune des présentations et à faire part de leurs observations. Au besoin, leur poser des questions telles que :
- Comment l’arrondissement et l’estimation facilitent-ils les calculs?
- Dans quel contexte peut-on estimer?
- Dans quel contexte peut-on arrondir?
- Qu’est-ce que vous pourriez écrire à ce sujet dans un journal de mathématiques (collectif ou personnel)?
S’assurer que les élèves comprennent qu’il est acceptable d’estimer et d’arrondir dans des contextes où l’on recherche une réponse approximative et non une réponse exacte.
Pour leur permettre de consolider les stratégies d’estimation, emmener les élèves dans un édifice de leur communauté pouvant accueillir un grand nombre de personnes (par exemple, aréna, salle de théâtre, église) et les inviter à y estimer le nombre de sièges. Il est également possible d’effectuer cet exercice à partir d’une visite virtuelle, sur Internet, d’une salle de théâtre ou d’une salle de spectacle.
Différenciation pédagogique
L’activité peut être modifiée pour répondre aux différents besoins des élèves.
| Pour faciliter la tâche | Pour enrichir la tâche |
|
|
Suivi à la maison
À la maison, les élèves peuvent :
- soit concevoir le plan d’une salle de spectacles sur du papier quadrillé et déterminer le nombre exact de sièges qu’elle contient;
- soit imprimer le plan d’une salle de spectacles obtenu à partir d’une recherche dans Internet et noter le nombre de sièges qu’elle contient.
De retour à l’école, les élèves échangent leur plan. Elles et ils estiment d’abord, à partir du plan reçu, le nombre de sièges dans la salle. Ensuite, elles et ils comparent leur estimation avec le nombre réel afin de déterminer si elle était appropriée.
Activité supplémentaire – Une autre perspective
Distribuer aux élèves une photo sur laquelle il y a une grande quantité d’objets, d’animaux ou de personnes (par exemple, photo d’une volée d’oiseaux, d’un champ de plants de maïs, d’abeilles autour d’une ruche, d’une foule) et leur demander d’estimer cette quantité. Les photos peuvent être obtenues, entre autres, sur Internet (par exemple, site d’un festival floral ou agricole, site de photographies de foules).
Puisque les photos offrent une perspective en 3 dimensions, les objets en premier plan apparaissent plus gros que ceux qui figurent à l’arrière-plan. Les élèves vont donc probablement avoir recours à des stratégies d’estimation différentes de celles utilisées dans la situation d’apprentissage. Les inciter à décrire et à justifier leur choix de stratégie.

Source: Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 181-189, 191-193.
