B2.10 Utiliser le raisonnement proportionnel pour identifier des situations proportionnelles et non proportionnelles.
Activité 1 : maquette à l’échelle
Cette activité intègre des concepts en Sens de l’espace, en sciences et technologie ainsi qu’en éducation artistique.
Le personnel enseignant explique qu’un fabricant de jouets lui a remis le croquis d’une de leurs maisons de poupée. Il présente aux élèves le croquis en s’attardant à ses dimensions et au fait qu’il est composé de prismes à base rectangulaire.
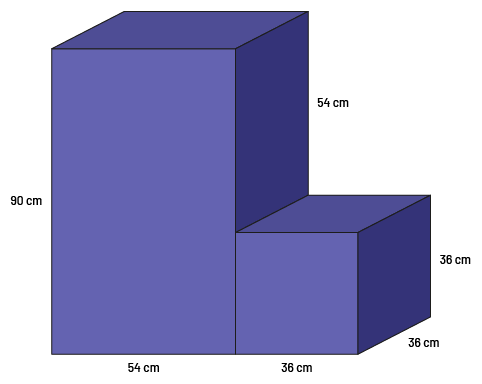 Image Un prisme rectangulaire et un cube sont accolés l’un à l’autre. Les mesures fournies pour le
prisme sont de
90 centimètres par 54 centimètres, et on sait que le haut du prisme qui ne touche pas au cube mesure 54 centimètres
de hauteur. Les mesures du cube sont de 36 par 36 par 36.
Image Un prisme rectangulaire et un cube sont accolés l’un à l’autre. Les mesures fournies pour le
prisme sont de
90 centimètres par 54 centimètres, et on sait que le haut du prisme qui ne touche pas au cube mesure 54 centimètres
de hauteur. Les mesures du cube sont de 36 par 36 par 36.
Ensuite, le personnel enseignant les invite à créer une maquette de cette maison qui comporte des mesures réduites de moitié (le rapport entre les mesures de la maquette et celles du croquis est de 1 à 2). Selon l’année d’études, les habiletés des élèves et les matériaux disponibles, d’autres rapports peuvent être donnés pour réaliser la maquette; par exemple, les mesures sont réduites au quart (rapport 1:4), aux 2 tiers (rapport 2:3) ou même doublées (rapport 2:1).
Après avoir formé des équipes de 2, le personnel enseignant leur distribue des grandes feuilles cartonnées (par exemple, carton bristol), des ciseaux, des règles, de la colle et du ruban-cache ou ruban adhésif, et leur alloue suffisamment de temps pour accomplir la tâche demandée (du temps peut aussi être accordé pour la décoration, si possible). Afin d’effectuer la tâche, les élèves peuvent tracer sur de grandes feuilles cartonnées le développement des 2 prismes à base rectangulaire. Ensuite, elles et ils les découpent et construisent leur maquette.
La tâche terminée, le personnel enseignant anime un échange en groupe classe qui met en valeur les diverses stratégies utilisées pour construire les maquettes.
Note : Cette activité pourrait être réalisée en se basant sur d’autres sortes de plans tels que le plan d’un pont, d’une tour, d’une machine simple ou d’un aménagement paysager.
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 108-109.
Activité 2 : proportionnelle oui ou non? (identifier les situations qui sont proportionnelles)
Préparer une série de languettes décrivant des situations qui sont proportionnelles et d’autres non. Diviser les élèves en dyade. Chaque équipe aura à faire un tableau comme ici-bas.
| Proportionnelle | Non proportionnelle | Justifications | Si oui, écrire le rapport |
|---|---|---|---|
Par la suite, les élèves doivent justifier leurs réponses. Pour les situations proportionnelles, elles et ils doivent écrire le rapport correspondant.
Faire un retour, en groupe classe. Mettre de l’importance sur les justifications des élèves.
Exemples de languettes :
- Une recette de pain dit qu’il faut ajouter 1 cuillérée à soupe de sucre à chaque 2 tasses de farine.
- Un mélange pour tondeuse à gazon nécessite 10 ml d’huile pour 3 litres d’essence.
- La sélectrice de l’équipe de ballon-panier choisit 1 personne sur 7, peu importe le nombre de candidates.
- Pedro mange un morceau de pizza dans chacun des formats différents de pizza.
- Une voiture se promène à une vitesse constante de 80 km/h.
- À chaque 5 dollars gagné, Myriam met 1 dollar de côté dans son compte d’épargne.
- Al investit 2 dollars dans un compte d’épargne et investit le double lors du prochain mois, puis le double lors du mois suivant, ainsi de suite.
Pour aller plus loin :
Faire une table de valeurs et une représentation graphique pour toutes les situations proportionnelles.
Activité 3 : le bon choix! (identifier la relation proportionnelle)
Diviser les élèves en équipes de 4 personnes. Projeter les 5 situations suivantes sur le tableau blanc. Individuellement, l’élève doit choisir 2 situations qui sont proportionnelles et ressortir ses arguments afin de justifier ses choix. Par la suite, chaque élève de l’équipe, à tour de rôle, doit convaincre les autres membres de son équipe concernant ses choix.
- Réussir la moitié des questions d’une évaluation.
- 3 bonnes réponses sur 5 questions.
- 5 questions réussies sur 7.
- 60 pour cent de réussite.
- Sur 40 questions, il y a eu 25 bonnes réponses.
