B2.4 Utiliser des objets, des schémas et des équations pour représenter, décrire et résoudre des situations relatives à l’addition et à la soustraction de nombres entiers.
Activité 1 : parlons entiers (équations pour représenter, décrire des situations relatives à l’addition et à la soustraction de nombres entiers)
Préparer des mises en situation afin que l’élève puisse décrire et représenter les contextes décrits sur les fiches (voir exemples ici-bas).
Organiser les pupitres de la classe en îlots. Chaque îlot représente une station de travail. Regrouper les élèves en équipes de 3. Faire une rotation des stations de travail.
Pendant le déroulement de l’activité, circuler, observer et écouter les interventions, commentaires des élèves. Noter si elles ou s’ils comprennent et peuvent décrire diverses situations impliquant des nombres entiers négatifs ou diverses façons de les représenter.
Faire un retour en groupe classe afin de voir s’il y a des différences au niveau des réponses des élèves.
Pour aller plus loin
Demander à chacune des équipes de rédiger une situation qui implique les entiers négatifs.
Station 1
Écris une équation qui représente la situation représentée par les jetons bicolores ci-dessous et invente une mise en situation qui pourrait l’expliquer.
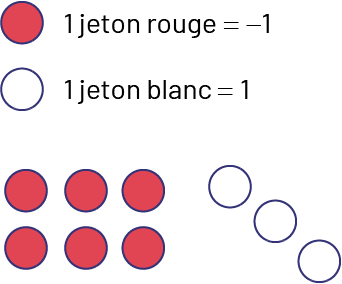
Station 2
Écris une équation qui représente la situation représentée sur la droite numérique ici-bas et invente une mise en situation qui pourrait l’expliquer.
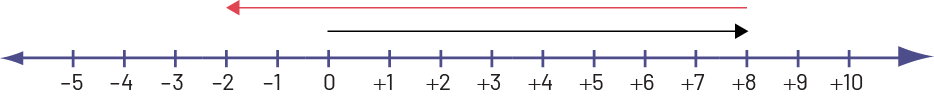
Station 3
Mise en situation
La ville de Kingston a une température moyenne de (–6) oC au mois de janvier. Celle de la première nation Fort Saverne est de (–22,5) oC.
Écris une équation qui te permet de trouver l’écart de température entre ces 2 endroits.
Station 4
Mise en situation
Au football canadien, les équipes tentent d’avancer sur le terrain dans le but de marquer un toucher. À l’occasion, les équipes reçoivent des pénalités et doivent ainsi reculer sur le terrain. Les longueurs sont mesurées en verge.
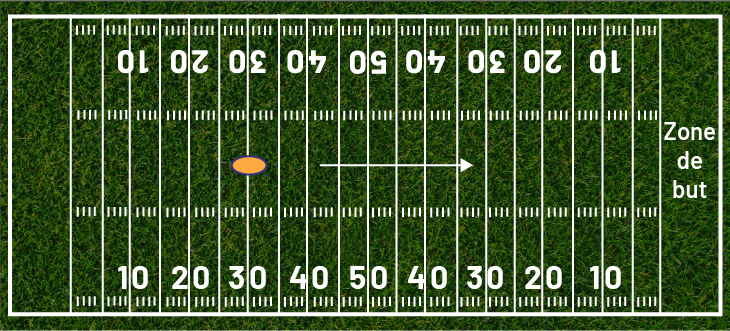 Image Illustration d’un terrain de football vu d’en haut. Il est gradué comme suit : dix, 20, 30, 40,
50, 40, 30, 20, dix. Le ballon se trouve sur la ligne 30 à gauche de 50. Une flèche part entre 40 et 45 avant 50,
traverse la ligne du 50, et se rend entre 35 et 30 après 50.
Image Illustration d’un terrain de football vu d’en haut. Il est gradué comme suit : dix, 20, 30, 40,
50, 40, 30, 20, dix. Le ballon se trouve sur la ligne 30 à gauche de 50. Une flèche part entre 40 et 45 avant 50,
traverse la ligne du 50, et se rend entre 35 et 30 après 50.
La remise en jeu se fait à partir de la ligne de 30 verges (voir ballon sur l’image). L’équipe offensive veut se rendre dans la zone des buts indiquée sur l’image ci-haut. Sur le jeu suivant, l’équipe offensive gagne 14 verges, mais reçoit une pénalité de 10 verges.
Écris une équation qui détermine à quel endroit sur le terrain le ballon sera déposé par les arbitres.
Station 5
Mise en situation
Pour le voyage de fin d’année des 7e, Zachary va au parc aquatique avec les élèves de sa classe. Il amène 20 $ pour dépenser. Arrivé là, il dépense tout son argent au dîner. Il emprunte 12 $ de son ami afin d’être capable de jouer à l’arcade.
Écris une équation qui représente cette situation et explique sa signification.
Station 6
Mise en situation
L’altitude se définit comme étant la hauteur par rapport au niveau de la mer. Une plongeuse se situe sur une plateforme qui se situe à 2 m d’altitude. Elle a comme mission de se rendre à une épave qui est dans le fond de la mer. Pour atteindre son objectif, de la plate-forme, elle saute à l’eau. Dans un premier temps, à partir de la surface d’eau, elle descend de 6 m et par la suite, descend un autre 7 m.
Écris une équation qui donne l’altitude de la plongeuse une fois rendue à l’épave. Explique sa signification.
Autres possibilités de station : pointage au golf, ascenseur, la bourse, thermomètre, puits de forage, lancement à la verticale d’un projectile dans les airs qui tombent dans l’océan.
Activité 2 : le bon choix (addition et soustraction de nombres entiers)
Donner une mise en situation « visuelle » et à partir de celle-ci présenter 3 choix. L’élève doit choisir celui qui décrit la situation et ensuite elle ou il doit justifier son choix.
Présenter les mises en situation sous forme de languettes et les placer dans une enveloppe (les mêmes mises en situation dans chaque enveloppe – 10 languettes par enveloppe).
Diviser les élèves en équipes de 3 et remettre une enveloppe par équipe.
Exemples de languettes
Languette 1
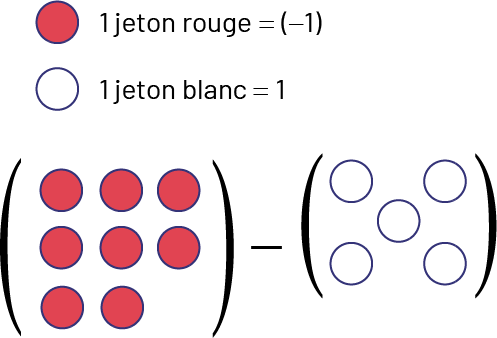 Image Deux ensembles de jetons sont présentés. Il y a un ensemble de
huit jetons rouges mis entre parenthèses, un symbole moins, puis un ensemble de cinq jetons blancs entre parenthèses.
La légende dit qu’un jeton rouge égale moins un, et qu’un jeton blanc égale un.
Image Deux ensembles de jetons sont présentés. Il y a un ensemble de
huit jetons rouges mis entre parenthèses, un symbole moins, puis un ensemble de cinq jetons blancs entre parenthèses.
La légende dit qu’un jeton rouge égale moins un, et qu’un jeton blanc égale un.
Lequel des énoncés décrit cette situation et donne la bonne réponse? Justifie ton choix.
- \(8\; - \;(- 5)\; = \;13\)
- \((- 8)\; - \;(- 5)\; = \; (- 3)\)
- \((- 8)\; - \;(+ 5)\; = \;(-13)\)
Languette 2

Lequel des énoncés décrit cette situation et donne la bonne réponse? Justifie ton choix.
- \((- 6)\; + \; 8\; = \; 2\)
- \((- 8)\; - \; 6\; = \; (- 14)\)
- \( + 6\; - \; 8\; = \;(- 2)\)
Activité 3 : plus ou moins (addition et soustraction de nombres entiers)
Formuler des équations avec les symboles + et – manquants. L’élève doit les compléter afin qu’elles soient vraies.
Donner quelques modèles d’équations clarifiant les attentes recherchées.
Par la suite, chaque élève formule 5 équations. Ramasser leurs équations. Diviser les élèves en équipes de 2 et leur remettre 10 problèmes aléatoires à résoudre.
*Encourager les élèves à utiliser du matériel de manipulation (jetons bicolores) ou la droite numérique afin de valider.
Observer et noter les commentaires des élèves. Faire un retour en groupe.
Exemples de questions d’objectivation
- Comment avez-vous procédé pour compléter vos équations? Comment avez-vous choisi les symboles?
- Est-ce que vous avez utilisé les jetons bicolores? Droites numériques? Pourquoi?
- Est-ce qu’une équation peut avoir plus d’une solution?
Exemples d’équations à compléter
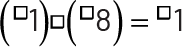
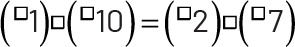 Image La séquence va comme suit : parenthèse ouvrante, case vide, un, parenthèse fermante, case vide,
parenthèse ouvrante, case vide, dix, parenthèse fermante, égale, parenthèse ouvrante, case vide, deux, parenthèse
fermante, case vide, parenthèse ouvrante, case vide, sept, parenthèse fermante.
Image La séquence va comme suit : parenthèse ouvrante, case vide, un, parenthèse fermante, case vide,
parenthèse ouvrante, case vide, dix, parenthèse fermante, égale, parenthèse ouvrante, case vide, deux, parenthèse
fermante, case vide, parenthèse ouvrante, case vide, sept, parenthèse fermante. 