B2.5 Additionner et soustraire des fractions, y compris en générant des fractions équivalentes, dans divers contextes.
Activité 1 : la fraction décisive (addition et soustraction de fractions équivalentes)
Préparer une série de mises en situation qui font appel à l’addition et à la soustraction de fractions. Diviser les élèves en équipes de 4. Distribuer une mise en situation à la fois. Chaque équipe doit proposer 2 démarches de résolution. Leur demander de les comparer et vérifier celle qui selon eux est la plus efficace. Les élèves doivent justifier leur choix. Faire un retour en groupe classe afin que les élèves puissent verbaliser leur analyse et leurs observations.
Exemples de mise en situation
Exemple 1
Arrivée à \(\frac{1}{4}\) du parcours, le coureur prend une boisson énergisante. L’autre point de rafraichissement se trouve à \(\frac{2}{8}\) plus loin sur le parcours. Quelle fraction de la course lui reste-t-il à courir après ce point de rafraichissement?
Exemple 2
Les élèves de 7e année proposent, à la direction d’école, un plan d’aménagement de la cour de récréation. Elles et ils divisent celui-ci en différents secteurs.
- Jardin : \(\frac{1}{{10}}\) de la superficie de la cour
- Terrain de soccer : \(\frac{6}{{15}}\) de la superficie de la cour
- Endroit pour modules de jeux extérieurs : \(\frac{2}{5}\) de la superficie
Quelle fraction de la superficie de la cour est considérée dans le plan d’aménagement des élèves?
Exemple 3
Pendant une journée typique du calendrier scolaire, Olivia dort \(\frac{3}{8}\) du temps et passe \(\frac{1}{3}\) de sa journée à l’école. De plus, elle danse pendant \(\frac{1}{{12}}\) de celle-ci. Quelle fraction de la journée lui reste-t-elle pour faire autre chose?
Exemple 4
Le charpentier doit couper 3 planches pour faire une bordure pour un jardin qui est derrière un cabanon. 2 des planches mesurent \(5\frac{3}{4}\) pieds chacune et l’autre mesure \(7\frac{2}{{16}}\) pieds. Quelle est la longueur totale des 3 planches?
Activité 2 : trouver l’intrus (addition et soustraction de fractions équivalentes)
Préparer un PowerPoint avec des exemples qui comprennent 4 images représentant des situations d’addition et de soustraction de fractions. L’élève doit analyser, prendre position et justifier pourquoi 1 des 4 images est considérée comme l’INTRUS. Les élèves partagent en petit groupe ou au groupe classe. Il est important d’écouter les commentaires des élèves afin de vérifier leur compréhension.
Note : Il y a plusieurs possibilités.
Exemple 1
Image Un rectangle est divisé en deux rangées de deux rectangles. La
description va de gauche à droite et de haut
en bas. Dans le premier rectangle, il y a un plein cercle violet, un cercle dont la moitié est violette, le tout
additionné
à un cercle dont un quart est violet. Dans le deuxième rectangle, il est écrit : un plus un demi plus un quart. Dans
le troisième rectangle, il y a un triangle bleu, un triangle dont la moitié est bleue, et un triangle dont le
tiers est bleu. Dans le quatrième rectangle, il y a une ligne graduée de zéro à cinq. Une flèche part de zéro et se
rend légèrement
après deux en indiquant un. Une flèche se rend de légèrement après deux à légèrement avant quatre en indiquant un
demi. Une flèche part de quatre et s’arrête à environ quatre virgule cinq en indiquant un quart. En dessous, il y a
une autre ligne graduée, de zéro à deux, au-dessus de laquelle il y a des marques d’intervalles aux cinquièmes
subdivisées par cinq, et sous laquelle il y a des marques d’intervalles aux quarts, subdivisées par quatre.
Justifications possibles des élèves :
- L’image en bas à gauche est l’intrus, car elle n’est pas équivalente aux 3 autres.
- Le contenu dans la case en haut à droite est l’intrus, car la représentation est seulement symbolique.
- Autres possibilités.
Exemple 2
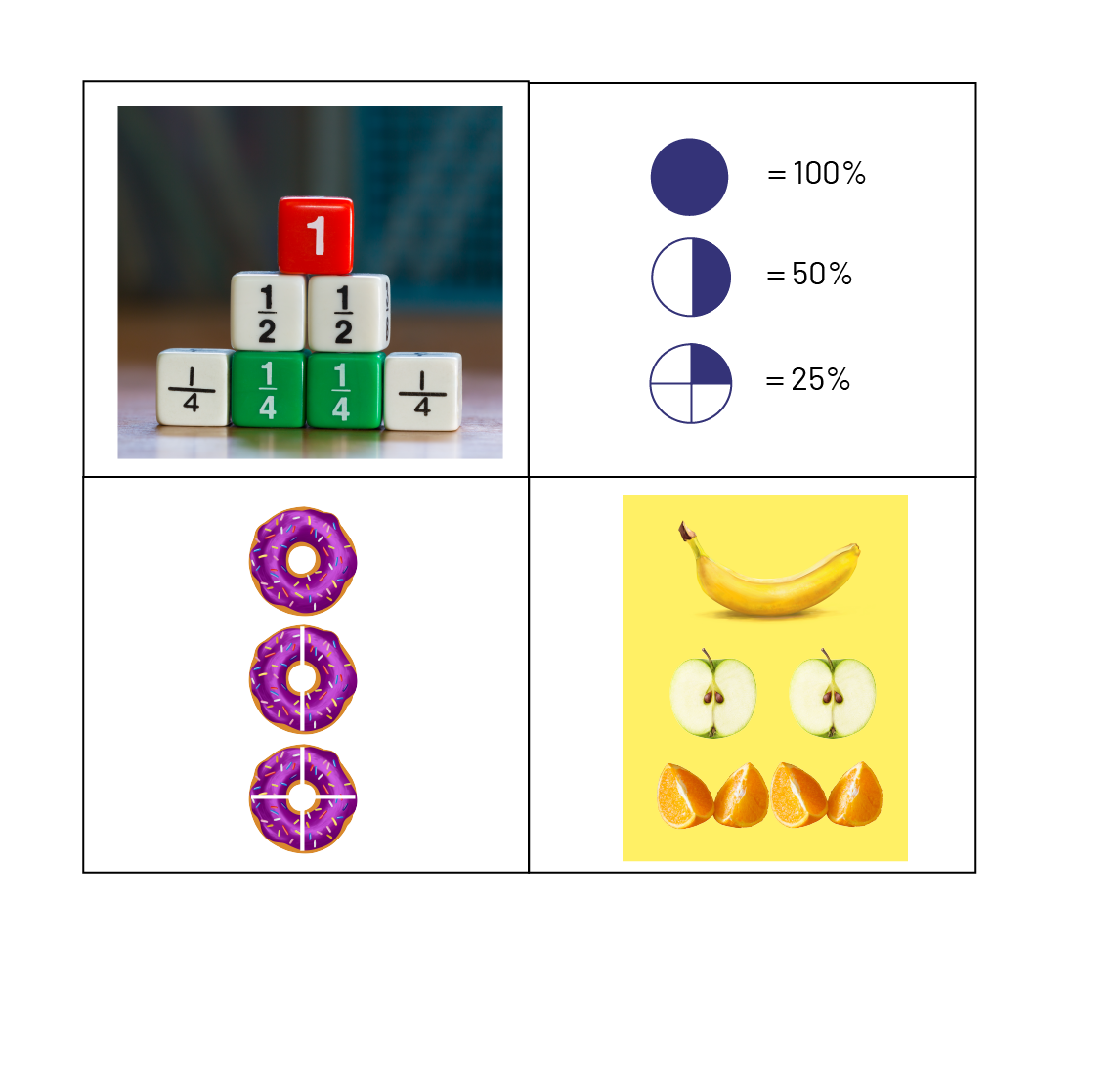Image Un rectangle est divisé en deux rangées de deux rectangles. La description va de gauche à droite et de haut
en bas. Dans le premier rectangle, il y a une pyramide de dés à jouer. Le dé du dessus est rouge et indique le
chiffre un.
Les deux dés du centre sont blancs et affichent tous deux un demi. Les quatre dés de la base vont comme suit : dé
blanc affichant un quart, deux dés verts affichant un quart, un dé blanc affichant un quart. Dans le deuxième
rectangle, il y a trois cercles placés l’un sous l’autre. Le premier est complètement bleu et
indique 100 pourcent. Le deuxième est à moitié bleu et indique 50 poucent. Le troisième au quart bleu et affiche 25
pourcent. Dans le troisième rectangle, il y a trois beignets identiques placés l’un sous l’autre. Le premier est
entier, le
deuxième est coupé en deux et le troisième est coupé en quatre. Dans le troisième rectangle, il y a une banane
au-dessus de deux demi-pommes au-dessus de quatre quarts d’orange.
Justification possible des élèves :
- L’image en haut à droite est l’intrus, car pour chaque image si on additionne les parties fractionnaires on obtient un tout équivalent à 1, mais pas celle-là.
Source : Inspiré du site https://wodb.ca