B1.1 Représenter et comparer des nombres naturels de 0 jusqu’à un milliard, y compris ceux exprimés sous forme développée à l’aide des puissances de 10, et décrire de quelles façons ils sont utilisés dans la vie quotidienne.
Habileté : représenter des nombres naturels de 0 jusqu’à un milliard
Le système de numération à base 10 couramment utilisé aujourd’hui dans bon nombre de pays fait appel à 10 symboles différents, soit les chiffres 0, 1, 2, 3, 4, 5, 6, 7, 8 et 9. C’est un système dit de position puisqu’une valeur différente est accordée aux symboles selon leur position dans un nombre. Par exemple, le chiffre 2 a une valeur de 2 unités dans le nombre 1 356 742, alors qu’il a une valeur de 20 000 unités dans le nombre 5 623 487. La compréhension des relations entre la valeur des chiffres et leur position dans un nombre est essentielle au développement du sens du nombre.
Au cycle primaire, les élèves développent une compréhension des relations entre les valeurs de position des unités, des dizaines et des centaines. Cependant, aux cycles moyen et intermédiaire, elles et ils ne transposent pas automatiquement cette compréhension aux plus grands nombres. C’est pourquoi le personnel enseignant doit s’assurer de leur faire comprendre que la valeur de n’importe quelle position dans un nombre est toujours 10 fois plus grande que la valeur de la position immédiatement à droite, et 10 fois plus petite que la valeur de la position immédiatement à gauche. Il est aussi important d’examiner les relations de 100 fois ou de 1 000 fois plus grand ou plus petit entre les valeurs de position afin de développer chez les élèves un sens du nombre approfondi, notamment le sens des grands nombres.
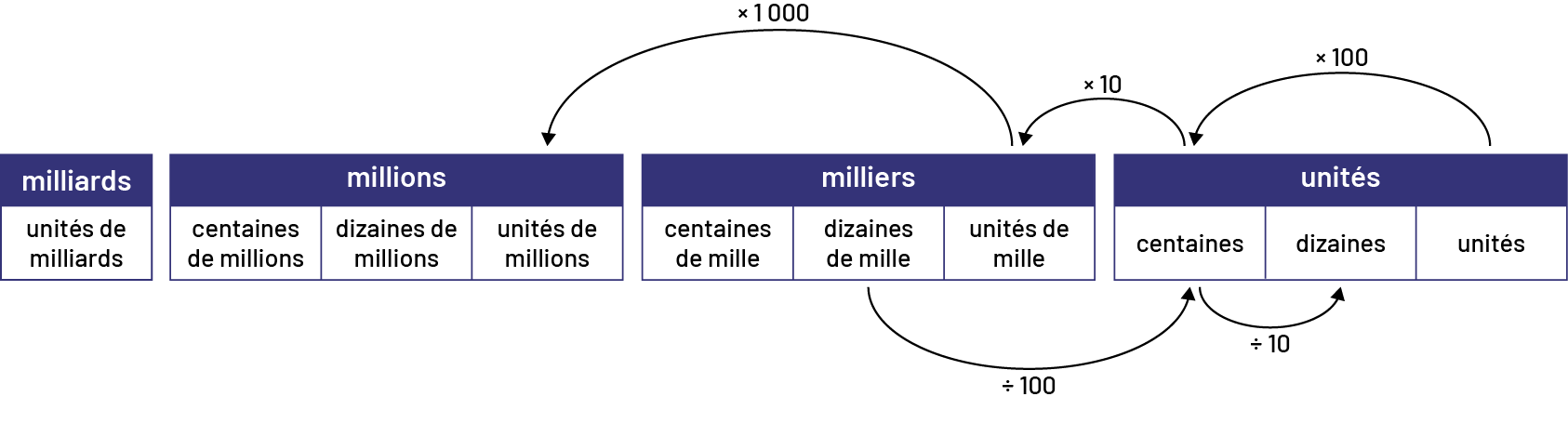 Image De gauche à droite, le schéma va comme suit : millions,
milliers, unités. Sous « millions », il est écrit «
unités de millions ». Sous « milliers », il est écrit « centaines de mille », « dizaines de mille » et « unités de
mille ». Sous « unités », il est écrit « centaines », « dizaines » et « unités ». En haut du schéma, l’on trouve trois
flèches courbes. La première part des unités de mille et se rend aux unités de
million avec la mention « fois mille ». La deuxième part des centaines et se rend aux unités de mille avec la
mention « fois dix ». La troisième part des unités et se rend aux centaines avec la mention « fois cent ». Sous le
schéma, il y a deux flèches courbes. La première part des dizaines de mille et se rend aux centaines avec
la mention « divisé par cent ». Et la deuxième part des centaines et se rend aux dizaines avec la mention « divisé
par dix ».
Image De gauche à droite, le schéma va comme suit : millions,
milliers, unités. Sous « millions », il est écrit «
unités de millions ». Sous « milliers », il est écrit « centaines de mille », « dizaines de mille » et « unités de
mille ». Sous « unités », il est écrit « centaines », « dizaines » et « unités ». En haut du schéma, l’on trouve trois
flèches courbes. La première part des unités de mille et se rend aux unités de
million avec la mention « fois mille ». La deuxième part des centaines et se rend aux unités de mille avec la
mention « fois dix ». La troisième part des unités et se rend aux centaines avec la mention « fois cent ». Sous le
schéma, il y a deux flèches courbes. La première part des dizaines de mille et se rend aux centaines avec
la mention « divisé par cent ». Et la deuxième part des centaines et se rend aux dizaines avec la mention « divisé
par dix ».
Les élèves doivent aussi reconnaître, par exemple, qu’une (1) dizaine de mille représente un regroupement de 100 centaines, un regroupement de 1 000 dizaines ou même un regroupement de 10 000 unités. Ces regroupements permettent de reconnaître des représentations équivalentes de nombres (par exemple, 2 534 est égal à 25 centaines et 34 unités).
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 44-45.
Les élèves doivent apprendre à représenter les nombres de diverses façons et à les reconnaître sous leurs multiples représentations. Ces habiletés les aident à établir des liens entre un nombre, sa représentation et la quantité qu’il représente. Il est donc essentiel d’exposer les élèves à différentes représentations des nombres. Il importe aussi de les exposer à divers contextes qui les mènent à représenter un nombre selon chacun des modes de représentation illustrés dans le schéma suivant ainsi qu’à passer d’un mode de représentation à un autre.
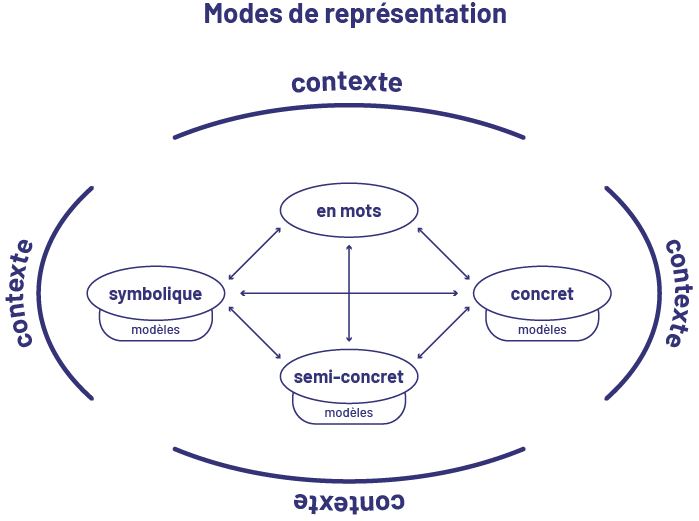 Image Le schéma s’intitule « Modes de représentation ». En haut, en bas, à gauche et à droite, il y a quatre arcs
qui, sans se toucher, forment une espèce d’ovale. Au-dessus du sommet de chaque arc est écrit le mot « contexte ».
Sous chaque creux d’arc apparaissent différents termes, disposés en forme de losange, chacun écrit dans un ovale.
En haut, l’ovale contient l’expression « en mots ». À droite, l’ovale contient le mot « concret ». Sous cet ovale
est écrit le mot « modèles ». En bas, l’ovale contient le mot « semi-concret ». Sous cet ovale est écrit le mot «
modèles ». Et à gauche, l’ovale contient le mot « symbolique ». Sous cet ovale est écrit le mot « modèles ». Tous les
termes sont reliés les uns aux autres par des flèches à double sens.
Image Le schéma s’intitule « Modes de représentation ». En haut, en bas, à gauche et à droite, il y a quatre arcs
qui, sans se toucher, forment une espèce d’ovale. Au-dessus du sommet de chaque arc est écrit le mot « contexte ».
Sous chaque creux d’arc apparaissent différents termes, disposés en forme de losange, chacun écrit dans un ovale.
En haut, l’ovale contient l’expression « en mots ». À droite, l’ovale contient le mot « concret ». Sous cet ovale
est écrit le mot « modèles ». En bas, l’ovale contient le mot « semi-concret ». Sous cet ovale est écrit le mot «
modèles ». Et à gauche, l’ovale contient le mot « symbolique ». Sous cet ovale est écrit le mot « modèles ». Tous les
termes sont reliés les uns aux autres par des flèches à double sens.
Le personnel enseignant doit être conscient de l’ordre dans lequel il exploite ces 4 modes de représentation avec les élèves. Baroody et Coslick (1998, p. 3-8 à 3-16) suggèrent de présenter un nouveau concept dans un contexte réel et significatif pour que les élèves puissent d’abord se créer des représentations à l’aide de mots, puis des représentations concrètes et semi-concrètes. Ce n’est que lorsqu’elles et ils auront développé une certaine compréhension du concept qu’elles et ils pourront passer à sa représentation symbolique. Les élèves doivent être en mesure d’établir des liens entre les représentations et de passer aisément d’une représentation à une autre.
Représentations à l’aide de mots
Le nombre est une représentation abstraite d’un concept très complexe. C’est pourquoi le rapport entre la façon de nommer un nombre et la quantité qu’il représente n’est pas évident pour les élèves. Plusieurs adultes croient à tort que si les élèves savent compter, elles et ils comprennent de facto le sens de chacun de ces nombres. Pourtant, un ou une élève peut bien être en mesure de lire et de nommer un nombre, par exemple 3 000 047, sans vraiment avoir un sens de la quantité qu’il exprime.
Au cycle moyen, les élèves apprennent à lire et à écrire en lettres les nombres jusqu’au million et au cycle intermédiaire, jusqu’à 1 milliard. Il ne faut pas sous-estimer les défis que pose l’écriture des nombres en lettres. Pour aider les élèves à surmonter ces défis, le personnel enseignant devrait inclure les nombres au mur de mots et construire avec eux des référentiels pour résumer les règles d’accord en nombre de 20, 100 et 1 000.
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 64-66.
Représentations symboliques
Les nombres sont représentés symboliquement à l’aide des chiffres qui les composent. Ils s’écrivent de gauche à droite par tranches de 3 chiffres qui constituent les billions, les milliards, les millions, les milliers et les unités. Chacune des tranches regroupe les centaines (c), les dizaines (d) et les unités (u).

Notes :
- En français, le terme « billion » n’a pas le même sens que le terme anglais billion. En français, un billion correspond à 1 000 milliards (\({10^{12}}\)) alors qu’en anglais il correspond à 1 000 millions (\({10^9}\)). En d’autres mots, le terme anglais billion correspond au terme français « milliard ».
- En français, l’écriture des nombres se fait en ajoutant un espace entre les tranches de 3 chiffres (par exemple, 13 567 232). Quoique l’écriture des nombres à 4 chiffres sans utiliser d’espace est acceptée (par exemple, 3543), l’écriture avec un espace (par exemple, 3 543) est privilégiée.
L’écriture des grands nombres nécessite une bonne maîtrise du concept de valeur de position, faute de quoi l’élève à qui l’on demande d’écrire symboliquement « mille deux cent treize » pourrait écrire 1 000 200 13 ou 1 000 213 ou 1 200 13. Elle nécessite aussi une compréhension du rôle du 0 pour indiquer l’absence d’une quantité dans une des positions.
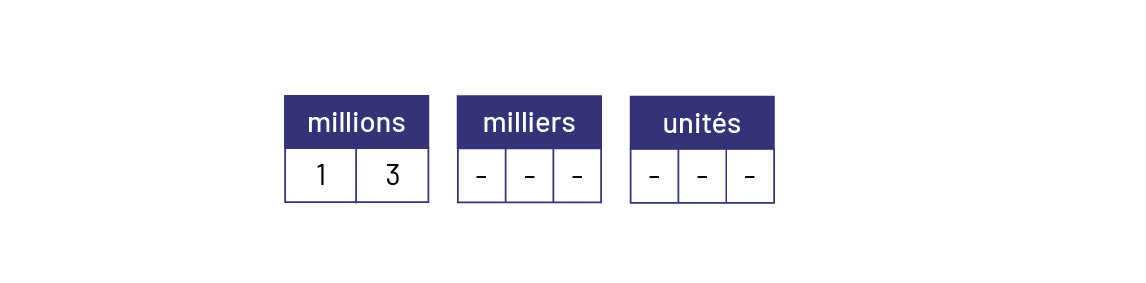
Voici un exemple d’un raisonnement que les élèves pourraient utiliser pour représenter symboliquement un grand nombre tel que « treize millions vingt-six mille quatre cents » :
- treize millions est représenté par 1 et 3 dans la tranche des millions, ce qui implique qu’il y a 6 positions à sa droite à combler;
- vingt-six mille est représenté par 2 et 6 dans la tranche des milliers, mais il faut insérer un 0 dans la position des centaines de mille, car dans le mot « cent » n’est pas entendu dans cette tranche du nombre;
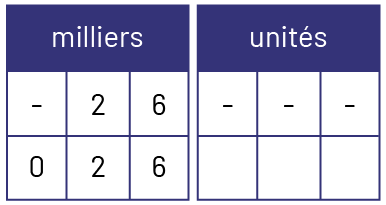 Image Deux tableaux de deux rangées de trois cases : milliers et unités. Le tableau des milliers se lit comme suit :
Tiret, deux six. Zéro, deux, six. Le tableau des unités contient trois tirets dans la première rangée et des cases
vides dans la deuxième rangée.
Image Deux tableaux de deux rangées de trois cases : milliers et unités. Le tableau des milliers se lit comme suit :
Tiret, deux six. Zéro, deux, six. Le tableau des unités contient trois tirets dans la première rangée et des cases
vides dans la deuxième rangée.
- quatre cents est représenté par un 4 dans la position des centaines de la tranche des unités. Puisqu’il n’y a aucune indication pour la position des dizaines et des unités, il faut ajouter deux 0 pour combler ces positions.
 Image Un tableau nommé « unités » possède deux rangées de trois cases. Dans la première rangée, on
trouve le chiffre quatre, un tiret et un tiret. Dans la deuxième rangée, on trouve le chiffre quatre, un zéro et un
zéro.
Image Un tableau nommé « unités » possède deux rangées de trois cases. Dans la première rangée, on
trouve le chiffre quatre, un tiret et un tiret. Dans la deuxième rangée, on trouve le chiffre quatre, un zéro et un
zéro.
- treize millions vingt-six mille quatre cents écrit symboliquement donne 13 026 400.
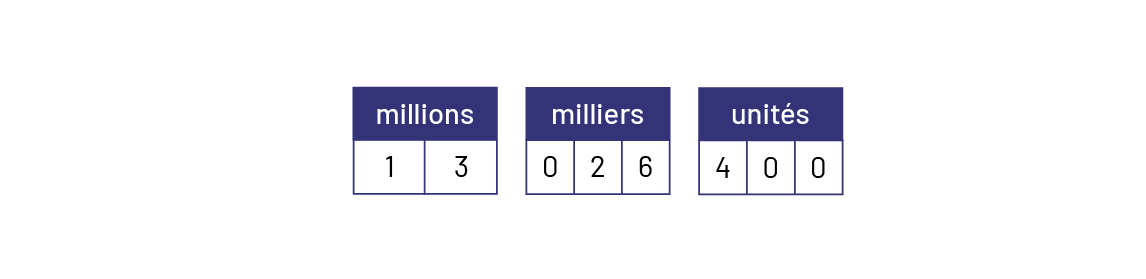 Image
Trois petits tableaux : millions, milliers et unités. Le tableau des millions possède les chiffres un et trois. Le
tableau des milliers possède les chiffres zéro, deux et six. Et le tableau des unités possède les chiffres quatre,
zéro, zéro.
Image
Trois petits tableaux : millions, milliers et unités. Le tableau des millions possède les chiffres un et trois. Le
tableau des milliers possède les chiffres zéro, deux et six. Et le tableau des unités possède les chiffres quatre,
zéro, zéro.
Un nombre peut être représenté de différentes façons à l’aide de symboles mathématiques, soit en respectant la valeur de la position de chaque chiffre (1 236 est égal à \(1\;000\; + \;200\; + \;30\; + \;6\)), soit d’après quelques valeurs de position (1 236 est égal à 12 centaines et 36 unités) ou encore en effectuant différentes opérations (1 236 est égal à \(1\;000\; + \;236\) ou \(1\;240\; - \;4\) ou \(1\;200\; + \;36\) ou \(1\;000\; + \;100\; + \;100\; + \;15\; + \;15\; + \;6\)). En fait, il existe une infinité de façons de représenter un nombre, chacune permettant aux élèves de se donner une autre façon de l’interpréter et d’en comprendre le sens.
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 70-71.
Relations d’égalité
Un nombre est représenté symboliquement à l’aide de chiffres. Par exemple, le nombre mille deux cent cinquante-six écrit symboliquement donne 1 256. Il peut aussi être représenté à l’aide de diverses expressions numériques. Par exemple, la représentation \(1\;000\; + \;200\; + \;50\; + \;6\) permet de reconnaître 1 256 en fonction de la valeur de position des chiffres qui le composent. Il y a de nombreuses autres façons de décomposer ou de représenter ce nombre.
 Image Un phylactère de pensée contient les opérations suivantes. 1 200
plus 56. 12 fois cent fois 56. Douze centaines plus 56 unités. 1 260 moins quatre. Parenthèse ouvrante un fois mille
parenthèse fermante plus parenthèse ouvrante deux fois cent parenthèse fermante plus parenthèse ouvrante cinq fois dix
parenthèse fermante plus six. 1 000 plus 60 moins quatre. Mille plus 256. Mille plus cent plus cent plus 25 plus 25
plus six. 1 255 plus un. Une unité de mille plus deux centaines plus cinq dizaines plus six unités.
Image Un phylactère de pensée contient les opérations suivantes. 1 200
plus 56. 12 fois cent fois 56. Douze centaines plus 56 unités. 1 260 moins quatre. Parenthèse ouvrante un fois mille
parenthèse fermante plus parenthèse ouvrante deux fois cent parenthèse fermante plus parenthèse ouvrante cinq fois dix
parenthèse fermante plus six. 1 000 plus 60 moins quatre. Mille plus 256. Mille plus cent plus cent plus 25 plus 25
plus six. 1 255 plus un. Une unité de mille plus deux centaines plus cinq dizaines plus six unités.
Les relations d’égalité permettent d’établir l’équivalence entre diverses représentations d’une même quantité. L’exploration des multiples représentations d’un nombre aide les élèves à acquérir une meilleure compréhension du sens de ce nombre. En situation de résolution de problèmes, les élèves doivent apprendre à choisir la représentation la plus appropriée au contexte et à l’intention.
Voici quelques exemples :
Pour comparer des nombres
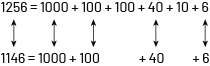 Image Deux équations sont écrites l’une sous l’autre en étant vis-à-vis. Première équation : 1
256 égale mille plus cent plus cent plus quarante plus dix plus six. Deuxième équation : 1 146 égale mille plus
cent plus quarante plus six. 1 256 et 1 146 sont liés par une flèche double sens. Tous les nombres de la
deuxième équation se lient au
même nombre de la première équation par des flèches double sens.
Image Deux équations sont écrites l’une sous l’autre en étant vis-à-vis. Première équation : 1
256 égale mille plus cent plus cent plus quarante plus dix plus six. Deuxième équation : 1 146 égale mille plus
cent plus quarante plus six. 1 256 et 1 146 sont liés par une flèche double sens. Tous les nombres de la
deuxième équation se lient au
même nombre de la première équation par des flèches double sens.
Pour calculer
\(\ 25\; \times \;9\; = \;25\; \times \;(10\; - \;1)\)
\(\ 25\; \times \;9\; = \;(25\; \times \;10)\; - \;(25\; \times \;1)\)
\(\ 25\; \times \;9\; = \;(250\; - \;25)\)
Alors \(\ 25 \times \;9\; = \;225\)
Pour faire un calcul mental
\(\begin{array}{l}325\; + \;527\; = \;325\; + \;525\; + \;2\\325\; + \;527\; = \;850\; + \;2\\325\; + \;527\; = \;852\end{array}\)
Pour estimer
\(\ 24\; \times \;26\) est près de \(\ 25\; \times \;25\)
\(\ 25\; \times \;25\; = \;25\; \times \;(20\; + \;5)\)
\(\ 25\; \times \;25\; = \;(25\; \times \;20)\; + \;(25\; \times \;5)\)
\(\ 25\; \times \;25\; = \;500\; + \;125\)
\(\ 25\; \times \;25\; = \;625\)
Ainsi, on peut donc dire que \(\ 24\; \times \;26\) est environ \(\ 625\)
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 48-49.
Les grands nombres peuvent être exprimés sous forme de nombres décimaux en exprimant la valeur de position en mots. Par exemple, 36,2 millions équivaut à 36 200 000 = \(36,2\; \times \;{10^6}\).
La forme développée avec des puissances de 10 montre un nombre sous forme d’expression en utilisant l’addition, la multiplication et les exposants. Le nombre « trois cent sept millions vingt mille cinquante » peut être exprimé comme 307 020 050 et \(3\; \times \;{10^8}\; + \;7\; \times \;{10^6}\; + \;2\; \times \;{10^4} + \;5\; \times \;10\).
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
Habileté : comparer des nombres naturels de 0 jusqu’à un milliard
Les nombres peuvent être comparés à l’aide de leur valeur de position ou en utilisant le raisonnement proportionnel. Par exemple, 1 milliard est 1 000 fois supérieur à 1 million.
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
Relations d’ordre
L’habileté à reconnaître des relations d’ordre s’acquiert en comparant des nombres, en les décomposant, en les plaçant en ordre croissant et décroissant, en comptant à rebours et en analysant la proximité relative de 2 nombres.
Au cycle intermédiaire, les élèves doivent reconnaître la relation d’ordre entre les nombres en les comparant. Elles et ils peuvent décrire la relation en précisant, par exemple, que 350 198 052 est plus petit que 432 840 590. Voici quelques exemples de stratégies qu’elles et ils peuvent utiliser pour comparer de grands nombres.
Comparaison des nombres 23 942 et 12 273
Les élèves peuvent reconnaître que 23 942 est plus grand que 12 273 :
- en ciblant une partie importante de chaque nombre (constater que 23 000 est plus grand que 12 000);
- en visualisant les quantités importantes (visualiser 23 regroupements de 1 000 et 12 regroupements de 1 000);

- en situant les nombres sur une droite numérique (le nombre 23 942 est situé à la droite du nombre 12 273);
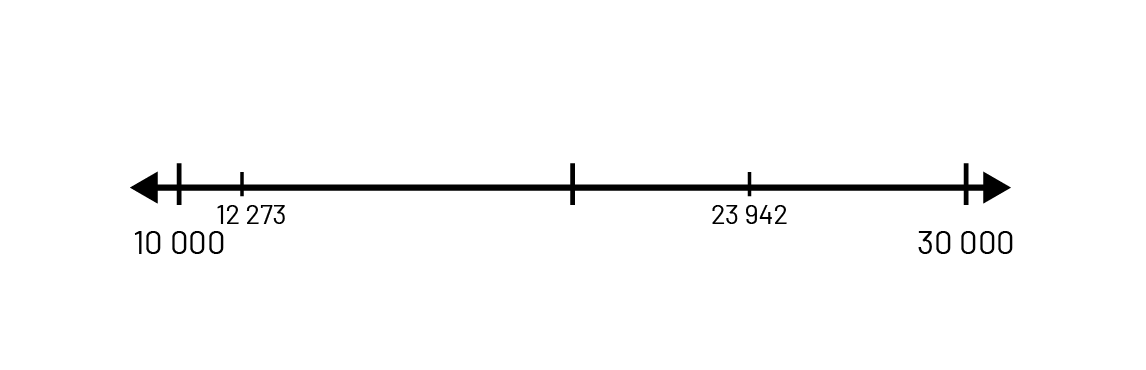 Image Une droite numérique est graduée de 10 000 à 30 000. Deux nombres ont été ajoutés : 12 273, qui
se situe légèrement à droite de 10 000, et 23 942, qui se situe environ au centre entre 20 000 et 30 000.
Image Une droite numérique est graduée de 10 000 à 30 000. Deux nombres ont été ajoutés : 12 273, qui
se situe légèrement à droite de 10 000, et 23 942, qui se situe environ au centre entre 20 000 et 30 000.
- en comparant les chiffres dans les diverses positions en partant de la gauche (le 2 représente 20 000 alors que le 1 représente 10 000);
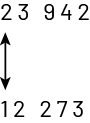
- en comparant les valeurs de position exprimées à l’aide de la puissance de 10.
| Shanghai | \[2\; \times \;{10^7}\; + \;7\; \times \;{10^6}\; + \;7\; \times \;{10^5} + \;9\; \times \;{10^4}\; + \;6\; \times \;{10^3}\] |
| Tokyo | \[3\; \times \;{10^7}\; + \;7\; \times \;{10^6}\; + \;3\; \times \;{10^5} + \;4\; \times \;{10^4}\] |
| Sao Paulo | \[2\; \times \;{10^7}\; + \;2\; \times \;{10^6}\; + \;2\; \times \;{10^5} + \;3\; \times \;{10^4}\; + \;7\; \times \;{10^3}\] |
| Delhi | \[3\; \times \;{10^7}\; + \;1\; \times \;{10^6}\; + \;1\; \times \;{10^5} + \;8\; \times \;{10^4}\; + \;1\; \times \;{10^3}\] |
Tokyo et Delhi ont une valeur à la position des dizaines de millions (107) plus élevée (3 dizaines de millions comparativement à 2 dizaines de millions)
Source : En avant, les maths! 7e année, CM, Nombres, p. 5.
Afin d’aider les élèves à développer l’habileté à reconnaître les relations d’ordre entre les grands nombres, le personnel enseignant peut, à partir d’un nombre donné, leur demander de compter par 1 (par exemple, 12 998, 12 999, 13 000, 13 001…) ou par intervalles (par exemple, 32 200, 32 400, 32 600…) et de compter à rebours par 1 (par exemple, 26 271, 26 270, 26 269…) ou par intervalles (par exemple, 45 650, 45 600, 45 550…).
Ces activités aident les élèves à reconnaître qu’en comptant par 1 ou par intervalles, tout nombre nommé est supérieur à ceux qui le précèdent et inférieur à ceux qui le suivent, alors qu’en comptant à rebours par 1 ou par intervalles, tout nombre nommé est inférieur à ceux qui le précèdent et supérieur à ceux qui le suivent. Bien que ces relations puissent sembler évidentes aux adultes, les élèves, pour leur part, se trompent souvent, car elles et ils ne tiennent pas compte du concept de regroupement. Par exemple, lorsqu’on leur demande quel nombre précède 300, plusieurs ont tendance à répondre spontanément 399 parce qu’ils portent leur attention sur les deux 0; ils savent qu’un nombre qui se termine avec deux 0 est toujours précédé d’un nombre qui se termine par deux 9 et elles et ils oublient de tenir compte du regroupement par centaines. En revanche, lorsque le même problème est posé en contexte, les élèves ont davantage tendance à donner des réponses réfléchies. Par exemple, dans une situation où un enfant a 300 cartes de hockey et qu’il en donne une, les élèves répondront facilement qu’il lui reste 299 cartes de hockey.
Une fois que les élèves maîtrisent les relations plus grand que et plus petit que, elle et ils doivent apprendre à préciser ces relations en faisant appel à leur compréhension du concept de quantité. Elles et ils emploient alors des expressions telles que : près de, environ, la même chose que, beaucoup plus que et un peu moins que. Par exemple, les élèves peuvent dire que la population d’un village de 15 239 habitants est d’environ 15 000 habitants; que 304 est un peu plus que 300; que 12 894 est un peu moins que 13 000; que 32 523 contient environ une centaine de plus que 32 432 et que 620 et 618 sont plus près l’un de l’autre que 630 et 680.
Cette habileté à préciser les relations d’ordre entre les nombres prend toute son importance lorsque les élèves utilisent les nombres en contexte de résolution de problèmes, d’arrondissement, d’estimation et de comparaison. L’activité suivante permet aux élèves de démontrer cette habileté.
Tracer au tableau une droite numérique pour représenter un intervalle quelconque (par exemple, de : 1 000 000 à 2 000 000). Placer quelques lettres (par exemple, A, B, C, D) dans cet intervalle tel qu’illustré ci-dessous.
 Image Une double droite numérique est graduée de mille à deux
mille avec une marque d’intervalle au centre. Entre mille et 1 500, au-dessus de la droite, on trouve la lettre «
A » puis les lettres « BC », ces deux dernières collées ensemble. Entre 1 500 et 2 000, au-dessus de la droite, on
trouve la lettre D.
Image Une double droite numérique est graduée de mille à deux
mille avec une marque d’intervalle au centre. Entre mille et 1 500, au-dessus de la droite, on trouve la lettre «
A » puis les lettres « BC », ces deux dernières collées ensemble. Entre 1 500 et 2 000, au-dessus de la droite, on
trouve la lettre D. Demander à quelques élèves de venir situer certains nombres sur la droite (par exemple, 1 873 000, 1 332 000, 1 167 000). Leur demander ensuite de décrire des relations d’ordre qui existent entre les nombres et les lettres.
Les élèves pourraient, par exemple, dire :
- que 1 167 000 se situe entre A et B;
- que les lettres B et C se situent entre 1 167 000 et 1 332 000;
- que le nombre 1 873 000 est plus près de 2 000 000 que de la lettre D;
- que la lettre B semble être plus au centre de l’intervalle entre 1 000 000 et 1 500 000 que la lettre C.
Source : adapté de Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 45-48.
Habileté : décrire de quelles façons les nombres sont utilisés dans la vie quotidienne
Le contexte est l’ensemble des informations entourant une situation donnée. Ces informations aident à cerner la situation dans laquelle les quantités sont utilisées et facilitent l’exercice d’un regard critique sur les nombres en question. En outre, le contexte facilite l’établissement de liens entre les nombres, les concepts mathématiques et le monde mathématisé. Pour toutes ces raisons, on préconise l’exploration des mathématiques en situation de résolution de problèmes.
Que veut dire 21 560 814 au juste? On parle de 21 560 814 « quoi »? Bref, un nombre sans contexte a peu de sens. C’est pourquoi on doit lui adjoindre des unités si on veut qu’il soit compris. Les élèves du cycle primaire ont déjà réalisé des activités avec les nombres dans différents contextes en utilisant diverses unités. Au cycle moyen et au cycle intermédiaire, on doit maintenir cette contextualisation afin de développer le sens des quantités, et ce, avec des nombres jusqu’à 1 milliard.
Un pas important à franchir est d’amener les élèves à comprendre que le même nombre représente la même quantité même si les contextes sont différents. Le nombre n’est qu’une représentation symbolique de la quantité. Si l’on a 100 000 pommes, 100 000 battements de cœur ou 100 000 immeubles, la quantité qu’est le regroupement de 100 000 ne change pas. Pourtant, si on demande aux élèves si elles ou s’ils croient qu’il y a plus de pommes que d’immeubles, un bon nombre risque de répondre qu’il y a plus d’immeubles que de pommes. Ils se sont attardés à l’espace occupé par les objets plutôt qu’à la quantité d’objets (100 000).
Il faut aussi que les élèves reconnaissent que selon le contexte de la situation donnée, différentes interprétations peuvent être dégagées d’une même quantité. Par exemple, pour des jeunes, une somme de 100 $ peut représenter beaucoup d’argent. Cependant, en contexte, le sens du nombre invite à nuancer : c’est beaucoup pour le prix d’un chandail, mais peu pour celui d’une bicyclette neuve. Le contexte change, mais la quantité demeure inchangée. De même, 200 000 blocs de bois représentent beaucoup de blocs, alors que 200 000 cheveux sur la tête équivalent à une chevelure moyenne. Ou encore, les élèves peuvent considérer que 13 ne représente pas une grande quantité, mais si on ajoute qu’il est le nombre de nos frères et sœurs, il prend une tout autre valeur. Ces exemples concrets et simples incitent à réfléchir et à analyser les quantités de façon critique.
À partir du cycle moyen et au cycle intermédiaire, la compréhension des nombres en contexte devient de plus en plus importante. Les élèves doivent commencer à porter des jugements critiques quant aux quantités et à faire preuve de discernement par rapport aux nombres. Les activités d’apprentissage doivent donc aider les élèves à développer d’autres habiletés, telles que reconnaître la vraisemblance d’un nombre donné, reconnaître qu’il s’agit d’une valeur exacte, ou au contraire, reconnaître qu’il s’agit d’un nombre approximatif provenant d’une estimation ou même d’un arrondissement. Le développement de ces habiletés peut être amorcé en ayant en classe des échanges sur le sens de nombres provenant de journaux et en discutant de leur signification réelle et de leur pertinence.
Le contexte permet aussi de reconnaître qu’un même nombre n’a pas toujours le même sens. En effet, lorsqu’il est question de nombres, l’interprétation courante les associe à la quantité, soit aux nombres cardinaux. Pourtant, en examinant le contexte, on remarque que certains nombres ne représentent pas des quantités, mais une position. C’est le cas des nombres ordinaux. Par exemple, lors d’un marathon, la coureuse ou le coureur qui est à la position 11 582 ne compte pas 11 582 objets. Le nombre indique la position d’une seule personne dans la série donnée. Les chiffres et les nombres sont aussi utilisés comme code d’identification. Les numéros d’assurance sociale, de codes à barres, de plaques d’immatriculation et d’adresses appartiennent à cette catégorie.
 Image Sous l’image d’un bac à sable, il est écrit : « Un million de grains de sable. Nombre cardinal. » Vue d’une
foule participant à un marathon de course sur un boulevard fermé pour l’occasion. Sous la photo, il est écrit : « Le
coureur portant un chandail rouge à la droite de l’image est au 11 582e rang.
Nombre ordinal. ». Un code à barres présente la série de chiffres suivante : zéro, un, deux, trois, quatre, cinq six,
sept, huit,
sept, neuf, zéro, deux.
Image Sous l’image d’un bac à sable, il est écrit : « Un million de grains de sable. Nombre cardinal. » Vue d’une
foule participant à un marathon de course sur un boulevard fermé pour l’occasion. Sous la photo, il est écrit : « Le
coureur portant un chandail rouge à la droite de l’image est au 11 582e rang.
Nombre ordinal. ». Un code à barres présente la série de chiffres suivante : zéro, un, deux, trois, quatre, cinq six,
sept, huit,
sept, neuf, zéro, deux.
Repères
De façon générale, un repère est une marque, un jalon, un élément de référence. Dans le cadre du développement du sens du nombre, l’utilisation de repères favorise la représentation mentale et, de ce fait, facilite la compréhension du nombre et de la notion du « combien ». Les repères, sans lesquels il est difficile de comprendre la quantité, sont des nombres ou des quantités aisément représentables mentalement puisque ceux-ci ont déjà été vus et manipulés. Les élèves auront de la difficulté à comprendre la quantité si elles ou s’ils n’utilisent pas de repères.
Les repères sont particulièrement utiles pour comprendre les grands nombres, puisqu’il est généralement impossible de reconnaître globalement ces quantités ou de les saisir par le dénombrement. Les élèves doivent alors s’en faire une idée en la comparant avec un repère. Par exemple, l’école vient de recevoir 10 000 feuilles pour des photocopies. Le concierge devrait-il ou devrait-elle demander de l’aide pour les transporter? Afin que les élèves puissent vraiment comprendre la situation et la quantité en jeu, elles et ils doivent se créer une image mentale de ce que 10 000 feuilles peuvent représenter. En utilisant un paquet de 500 feuilles comme repère, elles et ils peuvent imaginer cette quantité et appliquer la relation de proportionnalité pour déduire que 2 paquets contiennent 1 000 feuilles. Donc, 10 000 feuilles, ce sera 10 fois plus de paquets, soit 20 paquets de feuilles. On peut même reconnaître que 20 paquets équivalent à 2 boîtes de papier. La représentation mentale de l’espace qu’occupent ces 10 000 feuilles devient alors possible. Et la réponse à la question de départ, à savoir si le concierge devrait demander de l’aide pour transporter les feuilles, peut alors être débattue en toute connaissance de cause.
Les élèves doivent s’approprier des repères afin d’y avoir plus facilement recours selon le contexte et les nombres traités. Il n’existe pas de liste de repères. Ceux-ci sont personnels et proviennent des expériences vécues par chacun et chacune. Toutefois, les situations de la vie courante fournissent au personnel enseignant suffisamment d’occasions d’attirer l’attention de leurs élèves sur la quantité et la création de repères.
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 31-35.
Connaissance : forme développée
La forme développée montre un nombre sous forme d’expression en utilisant l’addition, la multiplication et les exposants.
Exemple
Le nombre trois cent sept millions vingt mille cinquante peut être exprimé comme 307 020 050 ou \(3\; \times {10^8}\; + \;7\; \times {10^6}\; + \;2\; \times {10^4}\; + \;5\; \times {10^1}\).
Connaissance : puissance de 10
Nombre 10 multiplié par lui-même le nombre de fois indiqué par l’exposant.
Exemple
\({10^2}\; = \;(10 \times 10 \;) = 100\)
Source : En avant, les maths! 7e année, CM, Nombres, p. 3.
