À vue d'oeil...

B1.4 Utiliser des fractions équivalentes pour réduire des fractions à leur plus simple expression, si nécessaire, dans divers contextes.

Habileté : utiliser des fractions équivalentes pour réduire des fractions à leur plus simple expression

---

Déterminer des fractions équivalentes, c’est déterminer des fractions qui représentent la même quantité. On cherche alors un nombre de « petites parties » d’un tout qui correspondent à un nombre particulier de « grandes parties » du même tout. Par exemple, si on cherche le nombre de seizièmes qui correspond à un quart (\(\frac{1}{4}\) = \(\frac{?}{{16}}\)) :

\(\frac{4}{{16}}\) de la même tablette de chocolat

\(\frac{1}{4}\) d’une tablette de chocolat

Les seizièmes sont 4 fois plus petits que les quarts. Dans un tout, il y a donc 4 fois plus de seizièmes que de quarts (\(4\; \times \;4\; = \;16\)). Afin de représenter la même quantité, il doit y avoir 4 fois plus de parties identifiées (\(4\; \times \;1\; = \;4\)). Donc, 4 seizièmes c’est équivalent à 1 quart. Voilà ce qui explique l’algorithme ci-dessous.

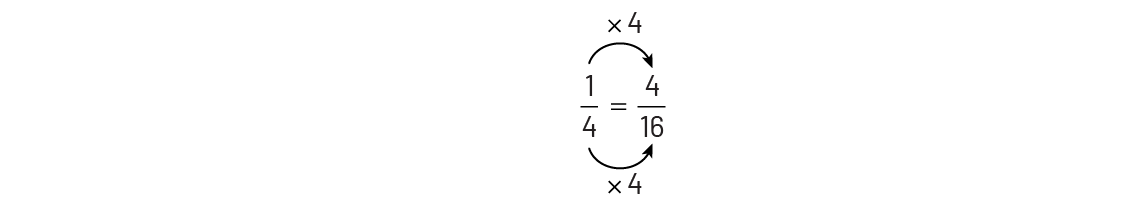Image Un quart égale quatre seizièmes. Une flèche relie le premier numérateur au second en indiquant multiplié par quatre. Une flèche relie le premier dénominateur au second en indiquant multiplié par quatre.

On peut voir que l’inverse est aussi vrai. Puisque les quarts sont 4 fois plus grands que les seizièmes, il en faut 4 fois moins (\(16\; \div \;4\; = \;4\)). Afin de représenter la même quantité, il doit y avoir 4 fois moins de parties identifiées (\(4\; \div \;4\; = \;1\)). Donc, 1 quart c’est équivalent à 4 seizièmes. Voilà ce qui explique l’algorithme ci-dessous.

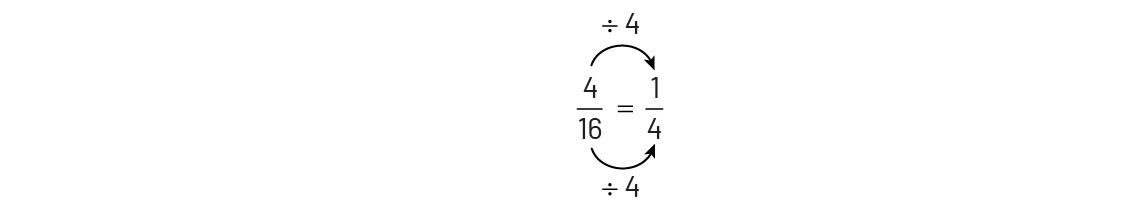Image Quatre seizièmes égale un quart. Une flèche relie le premier nominateur au second en indiquant divisé par quatre. Une flèche relie le premier dénominateur au second en indiquant divisé par quatre.

Il est essentiel que les élèves comprennent et puissent expliquer cette relation afin de donner un sens à l’algorithme utilisé pour déterminer des fractions équivalentes.

Source : Guide d'enseignement efficace des mathématiques de la 4^e à la 6^e année, p. 51.

Note : Une fraction est simplifiée lorsque le numérateur et le dénominateur n’ont aucun facteur commun naturel autre que 1. Le numérateur et le dénominateur sont des nombres naturels qui ne peuvent plus être réduits.

Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1^re à la 8^e année, 2020, Ministère de l’Éducation de l’Ontario.

Or, il n’est pas toujours aussi facile de reconnaître des fractions équivalentes. Prenons, par exemple, \(\frac{4}{6}\) et \(\frac{6}{9}\). On ne voit pas l’équivalence comme le résultat d’une multiplication du numérateur et du dénominateur par un nombre entier, soit l’algorithme usuel. On peut réduire chaque fraction à sa plus simple expression pour constater que chacune est équivalente à \(\frac{2}{3}\). On peut aussi faire appel à une représentation semi-concrète :

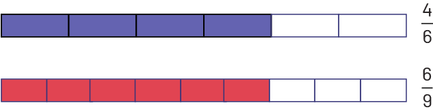Image Deux longs rectangles minces de la même longueur sont placés l’un sous l’autre en étant vis-à-vis. Le premier rectangle est divisé en six parties égales. Quatre d’entre elles sont violettes. À côté, il est écrit quatre sixièmes. Le deuxième rectangle est divisé en neuf parties égales. Six d’entre elles sont rouges, ce qui équivaut aux quatre parties violettes du haut. À côté du rectangle, il est écrit six neuvièmes.

Cette représentation permet de voir la relation multiplicative. On voit que les sixièmes sont une fois et demie plus grands que les neuvièmes. Pour passer des sixièmes aux neuvièmes, il faut donc 1,5 (\(1\frac{1}{2}\)) fois plus de morceaux. Cependant, ce type de situation est d’un niveau plus avancé que celui attendu au cycle intermédiaire.

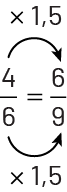Image Quatre sixièmes égale six neuvièmes. Une flèche relie le premier numérateur au second en indiquant multiplié par un virgule cinq. Une flèche relie le premier dénominateur au second en indiquant multiplié par un virgule cinq.

La relation d’équivalence doit aussi être explorée par rapport aux fractions d’un ensemble. Dans l’image ci-dessous, les élèves voient aisément que \(\frac{{12}}{{18}}\) des bonbons sont emballés dans des papillotes mauves. Toutefois, ils ont de la difficulté à déterminer d’autres fractions équivalentes (par exemple, \(\frac{2}{3}\), \(\frac{4}{6}\), \(\frac{6}{9}\)). Il importe alors de présenter des activités qui leur permettent de manipuler les éléments de l’ensemble. Ainsi, les élèves peuvent les grouper en ensembles de 6, de 3 ou de 2 et déterminer des fractions équivalentes.

Image Trois colonnes de six bonbons papillotes. Première colonne : un rouge, deux bleus, un rouge, deux bleus. Deuxième colonne : six bleus Troisième colonne : un bleu, quatre rouges, un bleu.

\(\frac{2}{3}\) des bonbons sont emballés dans des papillotes mauves.

\(\frac{4}{6}\) des bonbons sont emballés dans des papillotes mauves.

\(\frac{6}{9}\) des bonbons sont emballés dans des papillotes mauves.

L’expérience concrète avec les fractions équivalentes est le fondement du raisonnement proportionnel. On ne saurait lui accorder trop d’importance. C’est pourquoi le personnel enseignant doit planifier des activités qui reposent sur les notions informelles reliées aux fractions équivalentes.

Quelques remarques s’imposent par rapport à l’apprentissage des fractions équivalentes. Premièrement, il ne faut pas mettre l’accent sur le concept de fraction irréductible. Il est préférable de traiter ces fractions comme toutes les autres et de mettre l’accent sur les fractions équivalentes, c’est-à-dire sur les fractions qui sont des représentations différentes d’une même quantité. Deuxièmement, il faut accorder de l’importance au vocabulaire que l’on utilise et à la compréhension qu’en ont les élèves, ainsi qu’au vocabulaire que les élèves utilisent et comprennent. Par exemple, des élèves affirment que \(\frac{3}{4}\) et \(\frac{9}{{12}}\) sont des fractions équivalentes, mais que \(\frac{3}{4}\) est plus grand ou plus petit que \(\frac{9}{{12}}\), ou même qu’il s’agit d’une « meilleure » fraction. De même, certains élèves pensent que la fraction \(\frac{2}{3}\) est plus petite que la fraction \(\frac{4}{6}\), puisque \(\frac{2}{3}\) a été obtenu lorsqu’on a « réduit » \(\frac{4}{6}\). Il est important de déterminer la source des méprises des élèves et de chercher à corriger toute conception erronée.

Source : Guide d'enseignement efficace des mathématiques de la 4^e à la 6^e année, p. 52-53.