B2.2 Comprendre et se rappeler des pourcentages, des fractions et des nombres décimaux équivalents couramment utilisés.
Habileté : comprendre et se rappeler les pourcentages, les fractions et les nombres décimaux équivalents couramment utilisés
On sait qu’un nombre décimal représente une fraction dont le dénominateur est une puissance de 10 (par exemple, \(\ 0,3 = \frac{3}{10} \) ; \(\ 0,47 = \frac{{47}}{{100}}\)). Le concept de pourcentage étant intimement lié au concept de fraction, il n’y a qu’un pas à faire pour relier le pourcentage, le nombre décimal et la fraction décimale. À la fin du cycle moyen, les élèves qui ont acquis un bon sens du nombre peuvent passer d’une notation à une autre sans difficulté.
Exemple
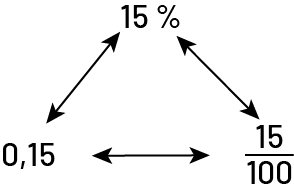 Image Nombres disposés en forme de triangle. En haut, 15 pourcent, en
bas à gauche, zéro virgule 15, et en bas à droite, 15 sur cent. Ils sont tous reliés entre eux par des flèches à
double sens.
Image Nombres disposés en forme de triangle. En haut, 15 pourcent, en
bas à gauche, zéro virgule 15, et en bas à droite, 15 sur cent. Ils sont tous reliés entre eux par des flèches à
double sens.
Pour aider les élèves à développer cette habileté, il faut régulièrement les inviter à exprimer leurs réponses en utilisant une autre notation. Par exemple, le personnel enseignant peut inciter l’élève qui a répondu que \(\frac{3}{4}\) des jeunes de la classe ont les cheveux noirs à exprimer aussi cette réponse en notation décimale (0,75) et en pourcentage (75 %).
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 50-51.
Repères
Les représentations mentales utilisées par les élèves sont renforcées par l’utilisation de repères. De façon générale, un repère est un élément de référence. Les repères utilisés pour l’étude des nombres décimaux et des pourcentages ressemblent à ceux employés pour l’étude des fractions. En créant des liens entre les nombres décimaux, les pourcentages et les repères fractionnaires, les élèves approfondissent leur sens du nombre.
Le tableau ci-après présente quelques repères qui devraient faire partie du bagage des élèves. Tout pourcentage peut être créé à l’aide des pourcentages repères.
Repères pour les fractions, les pourcentages et les nombres décimaux
| Fraction | Pourcentage | Nombre décimal | Exemple de représentation mentale |
|---|---|---|---|
| \(\frac{1}{{100}}\) | 1 % | 0,01 |  |
| \(\frac{1}{20}\) | 5 % | 0,05 |  |
| \(\frac{1}{10}\) | 10 % | 0,1 |  |
| \(\frac{15}{100}\) | 15 % | 0,15 |  |
| \(\frac{1}{4}\) | 25 % | 0,25 |  |
| \(\frac{1}{2}\) | 50 % | 0,5
|
 |
Ces repères, ainsi que les liens entre les fractions, les pourcentages et les nombres décimaux favorisent l’approfondissement du sens du nombre et s’avèrent fort utiles en situation de résolution de problèmes. L’habileté à passer d’une notation à une autre est avantageuse, car elle permet d’utiliser celle qui répond le mieux aux besoins du moment. Par exemple, un client qui veut calculer un rabais de 50 % sur le prix d’un article peut aisément le faire s’il reconnaît que 50 % équivalent à la moitié (\(\frac{1}{2}\)).
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 38-40.
Calculer 1 % (\(\frac{1}{{100}}\) ou 0,01) et 10 % (\(\frac{1}{{10}}\) ou 0,1) d’une quantité peut être fait mentalement en visualisant comment les chiffres d’un nombre changent de valeur de position.
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario
\(\begin{array}{l}10\;\% \;\;{\rm{de \;\;\; 23}}\;\\23\; \times \;0,1\; = \;2,3\end{array}\)
Je visualise un déplacement d’une colonne vers la droite dans le tableau de valeur de position.
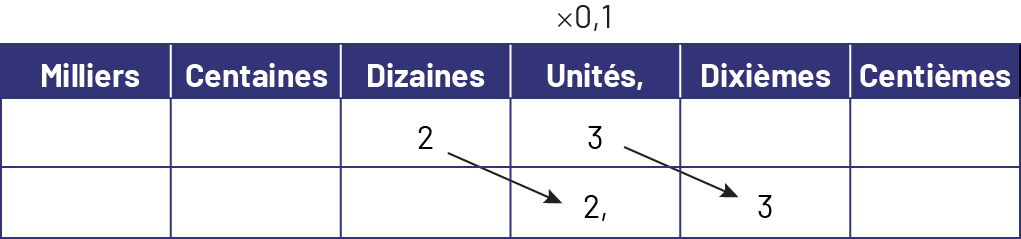 Image
Voici un tableau dont chaque colonne présente deux cases. Les colonnes vont comme suit : milliers, centaines,
dizaines, unités, dixièmes, centièmes. Dans la première case des dizaines, il y a le chiffre deux, relié par une
flèche à la deuxième case des unités laquelle contient aussi le chiffre deux. Dans la première case des unités, il y a
le chiffre trois, relié par une flèche à la deuxième case des dixièmes laquelle contient aussi le chiffre trois.
Toutes les autres cases sont vides. Au-dessus de la colonne unités, il est écrit fois zéro virgule un.
Image
Voici un tableau dont chaque colonne présente deux cases. Les colonnes vont comme suit : milliers, centaines,
dizaines, unités, dixièmes, centièmes. Dans la première case des dizaines, il y a le chiffre deux, relié par une
flèche à la deuxième case des unités laquelle contient aussi le chiffre deux. Dans la première case des unités, il y a
le chiffre trois, relié par une flèche à la deuxième case des dixièmes laquelle contient aussi le chiffre trois.
Toutes les autres cases sont vides. Au-dessus de la colonne unités, il est écrit fois zéro virgule un.
\(\begin{array}{l}1\;\% \;\;{\rm{de}}\;\;{\rm{\;23}}\\23\; \times \;0,01\; = \;0,23\end{array}\)
Je visualise un déplacement de 2 colonnes vers la droite dans le tableau de valeur de position.
 Image
Voici un tableau dont chaque colonne présente deux cases. Les colonnes vont comme suit : milliers, centaines,
dizaines, unités, dixièmes, centièmes. Dans la première case des dizaines, il y a le chiffre deux, relié par une
flèche à la deuxième case des dixièmes, qui est vide. Dans la première case des unités, il y a le chiffre trois, relié
par une flèche à la deuxième case des centièmes, qui est vide. Dans la deuxième case des unités, il y a un zéro avec
une virgule. Toutes les autres cases sont vides. Au-dessus du tableau, entre unités et dixièmes, il est écrit fois
zéro virgule zéro un.
Image
Voici un tableau dont chaque colonne présente deux cases. Les colonnes vont comme suit : milliers, centaines,
dizaines, unités, dixièmes, centièmes. Dans la première case des dizaines, il y a le chiffre deux, relié par une
flèche à la deuxième case des dixièmes, qui est vide. Dans la première case des unités, il y a le chiffre trois, relié
par une flèche à la deuxième case des centièmes, qui est vide. Dans la deuxième case des unités, il y a un zéro avec
une virgule. Toutes les autres cases sont vides. Au-dessus du tableau, entre unités et dixièmes, il est écrit fois
zéro virgule zéro un.
Les élèves croient souvent, à tort, qu’un pourcentage ne peut dépasser 100 (100 %). Or, certaines situations de la vie courante mènent à des pourcentages supérieurs à 100 %. Pour bien comprendre, ces situations peuvent être explorées au moyen de représentations concrètes ou semi-concrètes où les quantités sont mises en relation avec le tout. On peut aussi utiliser la notation fractionnaire ou décimale.
Exemple 1
À la suite d’une augmentation de 25 %, on peut affirmer que la nouvelle quantité représente 125 % de la quantité initiale.
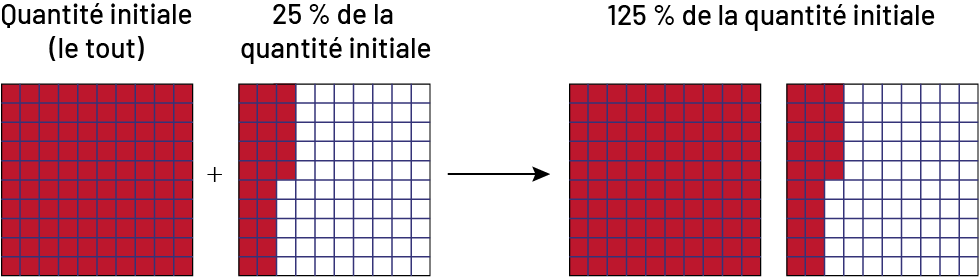 Image Quatre grilles de cent unités sont présentées côte à côte. La
première grille possède 100 unités rouges. Au-dessus, il est écrit : Quantité initiale, le tout. Entre la première et
la deuxième grille, il y a un symbole plus. La deuxième grille possède 25 unités rouges et 75 unités blanches.
Au-dessus, il est écrit : 25 pourcent de la quantité initiale. Elle se lie à la troisième grille par une flèche. La
troisième grille est identique à la première, et la quatrième grille est identique à la deuxième. Au-dessus des deux
dernières grilles, il est écrit : 125 pourcent de la quantité initiale.
Image Quatre grilles de cent unités sont présentées côte à côte. La
première grille possède 100 unités rouges. Au-dessus, il est écrit : Quantité initiale, le tout. Entre la première et
la deuxième grille, il y a un symbole plus. La deuxième grille possède 25 unités rouges et 75 unités blanches.
Au-dessus, il est écrit : 25 pourcent de la quantité initiale. Elle se lie à la troisième grille par une flèche. La
troisième grille est identique à la première, et la quatrième grille est identique à la deuxième. Au-dessus des deux
dernières grilles, il est écrit : 125 pourcent de la quantité initiale.
Ainsi, la nouvelle quantité représente \(\frac{{125}}{{100}}\) (125 centièmes) de la quantité initiale ou 125 % de la quantité initiale. Cependant, une augmentation de 125 % signifie que 125 % du tout est ajouté à la quantité initiale. La nouvelle quantité représente alors \(\frac{{225}}{{100}}\) (225 centièmes) de la quantité initiale ou 225 % de la quantité initiale.
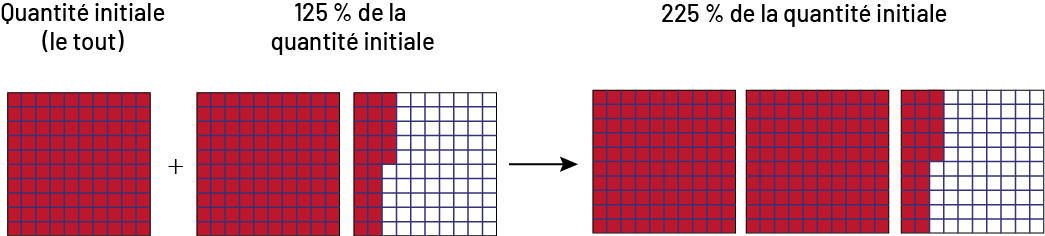 Image Six grilles de cent unités sont présentées côte à côte. La première grille possède 100 unités
rouges. Au-dessus, il est écrit : Quantité initiale, le tout. Entre la première et la deuxième grille, il y a un
symbole plus. La deuxième grille possède 100 unités rouges tandis que la troisième possède 25 unités rouges. Au-dessus
des deuxième et troisième grilles, il est écrit : 125 pourcent de la quantité initiale. La troisième grille se lie à
la quatrième par une flèche. La quatrième et la cinquième grilles possèdent 100 unités rouges, et la sixième possède
25 unités rouges. Au-dessus de ces trois dernières, il est écrit : 225 pourcent de la quantité initiale.
Image Six grilles de cent unités sont présentées côte à côte. La première grille possède 100 unités
rouges. Au-dessus, il est écrit : Quantité initiale, le tout. Entre la première et la deuxième grille, il y a un
symbole plus. La deuxième grille possède 100 unités rouges tandis que la troisième possède 25 unités rouges. Au-dessus
des deuxième et troisième grilles, il est écrit : 125 pourcent de la quantité initiale. La troisième grille se lie à
la quatrième par une flèche. La quatrième et la cinquième grilles possèdent 100 unités rouges, et la sixième possède
25 unités rouges. Au-dessus de ces trois dernières, il est écrit : 225 pourcent de la quantité initiale.
Exemple 2
Lors d’une collecte de fonds, les élèves de l’école L’Envolée se sont fixé un objectif de 2 000 $. À la fin de la collecte, elles et ils ont amassé 4 000 $. Quel pourcentage de leur objectif a été amassé?
\(\begin{array}{l}100\;\% \;\;{\rm{de}}\;\;{\rm{\;2}}\;{\;\rm{000}}\;{\rm{\$ }}\;\;{\rm{ = }}\;{\rm{2}}\;{\rm{000}}\;{\rm{\$ }}\\200\;\% \;\;{\rm{de}}\;\;{\rm{\;2}}\;{\;\rm{000}}\;{\rm{\$ }}\;\;{\rm{ = }}\;{\rm{4}}\;{\rm{000}}\;{\rm{\$ }}\end{array}\)
Puisque 100 % de la quantité équivaut à la quantité totale, soit 2 000 $, alors 200 % sont le double de cette quantité, soit 4 000 $.
Connaissance : nombre décimal
Un nombre décimal est un nombre qui peut être exprimé en notation décimale avec une partie décimale finie.
Exemple
\(3,72\;\;{\rm{et}} \; 12,135\;64\)
L’ensemble des nombres décimaux inclut tous les entiers, car ces derniers peuvent être exprimés avec une partie décimale.
Exemple
\(3\; = \;3,0\)
Il inclut aussi certaines fractions, comme \(\frac{2}{5}\) et \(\frac{3}{{16}}\), puisque \(\frac{2}{5}\; = \;0,4\;\)et \(\frac{3}{{16}}\; = \;0,187\;5\). On remarque alors que \(\frac{1}{2}\), \(\frac{5}{{10}}\) et \(0,5\) sont des représentations symboliques du même nombre décimal.
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 28.
Connaissance : fraction
Le mot fraction vient du latin fractio qui veut dire « rupture ». Une partie d’un objet brisé peut donc représenter une fraction, car c’est une partie d’un tout. Toutefois, pour déterminer une fraction d’un objet divisé en plusieurs parties, il faut que les parties soient équivalentes. Précisons que lorsqu’il est question de parties équivalentes, il ne s’agit pas nécessairement de formes identiques, bien que celles-ci soient plus faciles à utiliser. Les représentations de 1 quart (\(\frac{1}{4}\)) dans l’exemple ci-dessous sont basées sur l’aire du tout. Puisque chaque tout a une aire de 16 unités carrées, chaque quart (\(\frac{1}{4}\)) a une aire de 4 unités carrées. Malgré leurs formes différentes, chacun de ces quarts représente une partie équivalente d’un même tout.
Exemple
6 représentations équivalentes de 1 quart (\(\frac{1}{4}\)) du même tout.
 Image Six grilles de cinq points par cinq points sont disposées en deux rangées de trois. Nous
pouvons imaginer que
les points sont reliés horizontalement et verticalement pour former des carrés et
faciliter la description. Dans la première grille, quatre carrés dans le coin supérieur gauche sont verts. Dans la
deuxième grille, les quatre carrés de la première rangée sont en vert. Dans la troisième grille, le premier carré en
haut à gauche est en vert, le carré d’à côté est aux trois quarts
vert et le carré d’à côté est au quart vert. Le premier carré de la deuxième rangée est vert. Le premier carré de la
troisième rangée est aux trois quarts vert et le premier carré de la quatrième rangée est au quart vert. Dans la
quatrième grille, le deuxième et le troisième carré de la rangée du haut sont pleinement verts. Le premier
et le dernier carré de la rangée du haut sont à moitié vert, et le deuxième et le troisième carré de la deuxième
rangée sont à moitié vert. Le tout forme un triangle. Dans la cinquième grille, les trois premiers carrés de la
rangée du haut et le premier carré de la deuxième rangée
sont verts. Dans la sixième grille, les deux premiers carrés de la rangée du haut et le deuxième de la deuxième
rangée sont
pleinement verts. Le troisième carré de la rangée du haut et le premier carré de la deuxième rangée sont à moitié
verts.
Image Six grilles de cinq points par cinq points sont disposées en deux rangées de trois. Nous
pouvons imaginer que
les points sont reliés horizontalement et verticalement pour former des carrés et
faciliter la description. Dans la première grille, quatre carrés dans le coin supérieur gauche sont verts. Dans la
deuxième grille, les quatre carrés de la première rangée sont en vert. Dans la troisième grille, le premier carré en
haut à gauche est en vert, le carré d’à côté est aux trois quarts
vert et le carré d’à côté est au quart vert. Le premier carré de la deuxième rangée est vert. Le premier carré de la
troisième rangée est aux trois quarts vert et le premier carré de la quatrième rangée est au quart vert. Dans la
quatrième grille, le deuxième et le troisième carré de la rangée du haut sont pleinement verts. Le premier
et le dernier carré de la rangée du haut sont à moitié vert, et le deuxième et le troisième carré de la deuxième
rangée sont à moitié vert. Le tout forme un triangle. Dans la cinquième grille, les trois premiers carrés de la
rangée du haut et le premier carré de la deuxième rangée
sont verts. Dans la sixième grille, les deux premiers carrés de la rangée du haut et le deuxième de la deuxième
rangée sont
pleinement verts. Le troisième carré de la rangée du haut et le premier carré de la deuxième rangée sont à moitié
verts.
Il est important pour les élèves de comprendre que plus le tout est fractionné, plus ses parties sont petites
Exemple

Les quarts d’un tout sont plus gros que les dixièmes du même tout.
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 33.
Connaissance : pourcentage
Le pourcentage est une façon particulière de présenter une fraction. Il est souvent employé dans la vie courante. Une expression numérique comme 30 % (qui se lit « 30 pour cent ») est en réalité une autre notation du nombre 30 centièmes, soit \(\frac{{30}}{{100}}\) ou 0,30. Afin de faciliter la compréhension du concept de pourcentage, il faut d’abord amener les élèves à établir le lien entre le pourcentage et la fraction dont le dénominateur est 100, et ce, à l’aide de matériel concret ou semi-concret.
Exemple
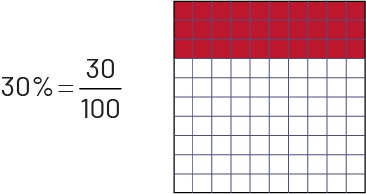
Les élèves doivent aussi réaliser qu’un pourcentage représente un rapport à 100 (par exemple, 30 % représentent le rapport 30 : 100). Il est important de souligner qu’un résultat exprimé en pourcentage ne signifie pas que la quantité en question est nécessairement composée de 100 parties, comme expliqué dans le tableau suivant.
| Représentation | Pourcentage | Notes pédagogiques |
|---|---|---|
 
|
75 % des cercles sont verts. | Même si 75 % des cercles sont verts, cela ne veut pas dire qu’il y a 100 cercles dans l’ensemble. Cependant, s’il y avait 100 cercles, il y aurait 75 cercles verts. De plus, la fraction des cercles qui sont verts est équivalente à \(\frac{{75}}{{100}}\)(par exemple, \(\frac{3}{4}\; = \;\frac{{75}}{{100}}\) et \(\frac{{150}}{{200}}\; = \;\frac{{75}}{{100}}\)). |
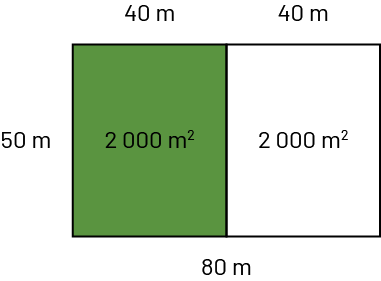 Image Un rectangle de 50 mètres par 80 mètres est découpé en deux parties égales sur la
largeur : une partie verte et une partie blanche. Ces deux dernières mesurent respectivement 2 000 mètres
carrés ainsi que 50 mètres par 40 mètres. Image Un rectangle de 50 mètres par 80 mètres est découpé en deux parties égales sur la
largeur : une partie verte et une partie blanche. Ces deux dernières mesurent respectivement 2 000 mètres
carrés ainsi que 50 mètres par 40 mètres.
|
50 % du terrain est recouvert de pelouse. | Même si 50 % du terrain est recouvert de pelouse, on ne peut pas affirmer que le terrain a une aire de
100 m2. Mais on peut affirmer que pour chaque 100 m2 de terrain,
50 m2 sont recouverts de pelouse. Ainsi, \(\frac{{2\;000}}{{4\;000}}\; = \;\frac{1}{2}\; =
\;\frac{{50}}{{100}}\; = \;50\;\% \).
|
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 34-35.
