B2.3 Utiliser des stratégies de calcul mental pour augmenter et diminuer un nombre naturel de 1 %, 5 %, 10 %, 25 %, 50 % et 100 %, et expliquer les stratégies utilisées.
Habileté : utiliser des stratégies de calcul mental pour augmenter et diminuer un nombre naturel de 1 %, 5 %, 10 %, 25 %, 50 % et 100 %
Représentation mentale
Les élèves doivent être capables de se créer une représentation mentale d’un pourcentage, comme ils le font pour les nombres décimaux. La nature même du pourcentage leur permet de visualiser plus facilement une quantité, car il s’agit toujours d’un rapport avec 100. Il faut aussi bien comprendre qu’un pourcentage est une autre façon de représenter une quantité.
Exemple
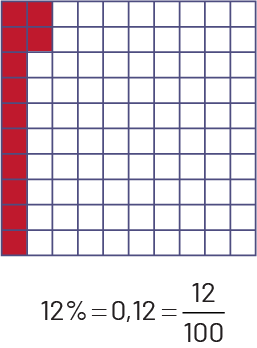Image Une grille de cent unités possède 12 unités rouges et le reste
en blanc. Sous la grille il est écrit : douze pourcent égale zéro virgule douze égale douze sur cent.
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 37.
Repères
Les représentations mentales utilisées par les élèves sont renforcées par l’utilisation de repères. De façon générale, un repère est un élément de référence. Les repères utilisés pour l’étude des nombres décimaux et des pourcentages ressemblent à ceux employés pour l’étude des fractions. En créant des liens entre les nombres décimaux, les pourcentages et les repères fractionnaires, les élèves approfondissent leur sens du nombre.
Le tableau ci-après présente quelques repères qui devraient faire partie du bagage des élèves.
Repères pour les fractions, les pourcentages et les nombres décimaux
| Fraction | Pourcentage | Nombre décimal | Exemple de représentation mentale |
|---|---|---|---|
| \(\frac{1}{{100}}\) | 1 % | 0,01 |  |
| \(\frac{1}{20}\) | 5 % | 0,05 |  |
| \(\frac{1}{10}\) | 10 % | 0,1 |  |
| \(\frac{15}{100}\) | 15 % | 0,15 |  |
| \(\frac{1}{4}\) | 25 % | 0,25 |  |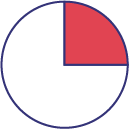
| \(\frac{1}{2}\) | 50 % | 0,5
|
 |
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 39.
Calcul mental
La vie quotidienne présente de nombreuses occasions d’effectuer des opérations sur les pourcentages. Par exemple, la taxe de vente provinciale sur les achats et les données sportives font appel aux pourcentages. L’habileté à estimer et l’habileté à calculer mentalement sont des caractéristiques du sens du nombre et du sens des opérations. Diverses stratégies de calcul mental peuvent être utilisées dont l’arrondissement, la décomposition et l’utilisation de repères. Voici quelques exemples de leur utilisation en situation de calcul mental.
Décomposition et arrondissement à l’aide des repères
Exemple 1
Abdul achète une salade et un jus pour son dîner. Le coût est 9 $ plus 13 % de taxe de vente provinciale. Approximativement combien coûtera le dîner d’Abdul?
Afin de connaître le coût approximatif de son dîner, Abdul peut :
- Arrondir au dollar près (10 $).
- Le coût total augmentera, car la taxe est ajoutée au montant du dîner.
- Arrondir au pourcentage repère supérieur près (15 %); l’élève peut décomposer le 15 %= 10 % et 5 % et ensuite calculer les montants 10 % de 10 $ + 5 % de 10 $ (moitié du 10 %) = 1 $ + 0,50 $ =1,50.
- Additionner le coût et la taxe (10 $ + 1,50 $ = 11,50 $).
*Arrondir le coût ainsi que la taxe de vente provinciale permet à Abdul de connaître le total approximatif de son dîner.
Exemple 2
Une gérante achète une machine en rabais de 25 %. La machine coûte 184 $. Combien d’argent la gérante épargnera-t-elle?
Le coût total diminuera, car il y a un rabais.
Décomposer 184 \((\ 100 + 80 + 4 \)).
Équivalence : \(\ \;25\;\% = \frac{1}{4}\).
Calcul
25 % de 100 $ est 25 $
25 % de 80 $ est 20 $
25 % de 4 $ est 1 $
La gérante épargnera 25 $ + $ 20 + $ 1 = 46 $.
Décomposition
Dans cette vidéo, les élèves réfléchissent, partagent et développent différentes stratégies de calcul mental en lien avec le calcul de pourcentages.
Description de la vidéo
Description à venir
Utilisation de repères
Exemple
Au cours des 10 dernières années, la polyvalente a une diminution de 30 % au niveau des inscriptions d’élèves. Il y avait 800 élèves d’inscrits. Combien d’élèves sont présentement inscrits?
Une diminution amène une soustraction; le nombre d’élèves sera plus bas.
Décomposer le 30 % en utilisant les repères (exemple : \(25\;\% \; + \;5\;\% \)).
25 % représentent le quart du total, donc diviser \(\frac{{800}}{4}\; = \;200\) élèves.
5 % sont la moitié de 10 %, donc \(10\;\% \; = \;\frac{1}{{10}}\), diviser 800 par 10 = 80 élèves et diviser 80 élèves par 2 pour obtenir le 5 % qui équivaut à 40 élèves.
Donc, il y a une diminution de 240 élèves ce qui veut dire qu’il y a maintenant 560 élèves d’inscrits.
Utiliser la valeur de position
Exemple
Un magasin annonce que la moyenne de ses ventes quotidiennes a augmenté de 10 % comparativement à la semaine dernière. La moyenne des ventes était de 1 250 $ la semaine dernière. Quelle est la moyenne des ventes de cette semaine?
Augmentation des ventes, donc la valeur sera plus grande :
- Le montant 1 250 $ représente le 100 % et l’ajout est le 10 %.
- 10 % sont égaux à 0,1.
- Pour calculer l’ajout (10 % de plus) : décomposer le 1 250 (\(1\;000\; + \;100\; + \;100\; + \;50\)).
- 0,1 de 1 000 sont 100 (autre option: \(0,1\; = \;\frac{1}{{10}}\), donc diviser le montant par 10).
- 0,1 de 100 sont 10 (2 fois).
- 0,1 de 50 (moitié de 100) sont 5.
Le 10 % de plus équivaut à 125 $ donc le montant des ventes est de 1 375 $.
Connaissance : pourcentage
Le pourcentage est une façon particulière de présenter une fraction. Il est souvent employé dans la vie courante. Une expression numérique comme 30 % (qui se lit « 30 pour cent ») est en réalité une autre notation du nombre 30 centièmes, soit \(\frac{{30}}{{100}}\) ou 0,30. Afin de faciliter la compréhension du concept de pourcentage, il faut d’abord amener les élèves à établir le lien entre le pourcentage et la fraction dont le dénominateur est 100, et ce, à l’aide de matériel concret ou semi-concret.
Exemple
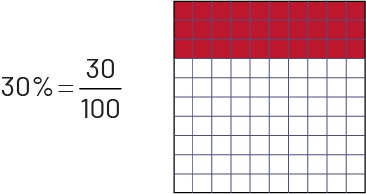Image À côté de l’équation trente pourcent égale trente sur cent, il y
a une grille de cent unités où les trois premières rangées de dix carrés sont rouges, et le reste est blanc.
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 34.
Connaissance : calcul mental
La plupart des calculs effectués au quotidien sont reliés à un calcul mental. Les personnes qui acquièrent de bonnes habiletés de calcul mental ne dépendent pas de l’électronique ou du papier pour effectuer les calculs de la vie courante. Or, il est important de démystifier le calcul mental. « Le calcul mental consiste à effectuer des calculs sans l’aide ou presque d’un crayon et d’un papier, ou d’une calculatrice. Il représente une composante essentielle d’un enseignement efficace. » (Ministère de l’Éducation de l’Ontario, 2004 a, p. 24) Ainsi, il ne s’agit pas d’utiliser un algorithme dans sa tête, mais de calculer avec souplesse et efficacité.
Selon les situations, on fait appel au calcul mental pour déterminer des résultats approximatifs ou exacts. On estime souvent mentalement lorsque c’est l’ordre de grandeur qui est recherché. Par exemple, pour avoir une idée du coût de la taxe de ses achats, on utilise des nombres plus simples. Il est important aussi de savoir calculer mentalement avec précision (par exemple, un serveur qui doit rendre la monnaie à un client). Plusieurs stratégies de calcul mental sont basées sur la relation entre le tout et ses parties (décomposition et regroupement), sur l’établissement de relations entre les nombres et sur les propriétés des opérations. Souvent, ces stratégies proviennent d’un transfert de modèles utilisés au cours de l’apprentissage des opérations.
Exemple
Arrondir :
1,2 % de 100
1 % de 100 est 1
1,2 % de 100 est un peu plus de 1
Utiliser des repères :
23 % de 400
25 % de 400 est 100
23 % de 400 est un peu moins de 100
Utiliser les valeurs de position :
10 % de 500
10 % = 0,1
0,1 de 500 sont 50
Décomposer les nombres :
50 % de 355
50 % de 300 = 150
50 % de 50 = 25
50 % de 5 = 2,5
\(150\; + \;25\; + \;2,5\; = \;177,5\)
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 111-112.