B2.6 Déterminer le plus grand facteur commun pour une variété de nombres naturels jusqu’à 144 ainsi que le plus petit commun multiple pour 2 ou 3 nombres naturels.
Habileté : déterminer le plus grand facteur commun pour une variété de nombres naturels jusqu’à 144 ainsi que le plus petit commun multiple pour 2 ou 3 nombres naturels
L’habileté à reconnaître qu’un nombre est premier ou composé, s’il est pair ou impair ou s’il est divisible par un nombre quelconque peut faciliter l’élève à utiliser diverses stratégies pour trouver le plus petit commun multiple ou le plus grand facteur commun de nombres naturels.
Multiple d’un nombre
Un multiple d’un nombre naturel correspond au produit de ce nombre par un autre nombre naturel. Par exemple, le nombre 12 est un multiple de 4 parce que \(12\; = \;4\; \times \;3\). Il est aussi un multiple de 1 (\(12\; = \;1\; \times \;12\)), de 2 (\(12\; = \;2\; \times \;6\)), de 3 (\(12\; = \;3\; \times \;4\)), de 6 (\(12\; = \;6\; \times \;2\)) et de 12 (\(12\; = \;12\; \times \;1\)). Les élèves doivent être en mesure de déterminer si un nombre est un multiple ou pas d’un autre nombre (par exemple, « Est-ce que 42 est un multiple de 7? »). Elles et ils doivent aussi être capables de dresser une liste des multiples d’un nombre quelconque (par exemple, les multiples de 7 sont : 7, 14, 21, 28, 35, 42, 49…). La liste des multiples d’un nombre est infinie. L’important n’est donc pas de connaître par cœur une liste partielle de ces multiples, mais bien de pouvoir en produire une au besoin.
Note : Conformément à la définition d’un multiple d’un nombre, le nombre 0 est un multiple de tout nombre naturel. Par exemple, 0 est un multiple de 7 puisque \(7\; \times \;0\; = \;0\). Cependant, ce cas particulier n’est habituellement pas retenu lorsqu’on demande d’énumérer la liste des multiples d’un nombre naturel quelconque. Dans plusieurs situations, il est utile d’identifier un multiple qui est commun à 2 nombres. La recherche d’un tel multiple commun, qui consiste habituellement à comparer les listes de multiples de chacun des 2 nombres, devrait se faire dans un contexte de résolution de problèmes.
Exemple
Un élève sonne une cloche toutes les 6 secondes et une élève siffle toutes les 8 secondes.
a) Quand produiront-ils leurs sons en même temps pour la 1re fois?
b) À quels autres moments les sons coïncideront-ils?
Pour résoudre ce problème, les élèves peuvent construire une table de valeurs ou écrire une liste des multiples de 6 (6, 12, 18, 24…) et de 8 (8, 16, 24, 32…). Elles et ils seront alors en mesure de déterminer que les 2 élèves produiront leurs sons en même temps pour la 1re fois à la 24e seconde. Ceci est le plus petit commun multiple (PPCM).
| Nombre de sons | 1 | 2 | 3 | 4 | … |
|---|---|---|---|---|---|
|
Son de la cloche |
6 | 12 | 18 | 24 | |
|
Son du sifflement |
8 | 16 | 24 | 32 |
Pour répondre à la 2e question, elles et ils doivent établir l’ensemble des prochains multiples communs de 6 et de 8, soit 48, 72, 96… Même si le concept de plus petit commun multiple (PPCM) fait l’objet d’un contenu d’apprentissage en 7e année seulement, plusieurs problèmes en algèbre au cycle moyen impliquent la recherche d’un multiple commun de 2 nombres.
Facteur et diviseur d’un nombre
Dans une multiplication de 2 ou de plusieurs nombres naturels, chacun de ces nombres est appelé un facteur du nombre qui constitue le produit. Par exemple, 2 et 8 sont des facteurs de 16.
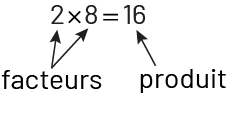
Note : Si on veut énumérer tous les nombres naturels qui sont des facteurs de 16, il faut ajouter 1, 4 et 16 puisque \(\ 1 \times 16 = 16\) et que \(\ 4 \times 4 = 16\).
Dans une division, la relation entre le dividende et le diviseur donne un quotient. Un nombre naturel est dit être un diviseur d’un autre nombre naturel si leur quotient est un nombre entier. Ainsi, 3 est un diviseur de 21 puisque le quotient donne l’entier 7.
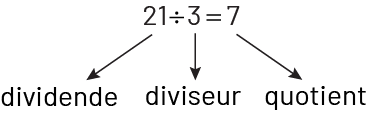
Note : Si on veut énumérer tous les diviseurs possibles de 21, il faut ajouter 1, 7 et 21 puisque \(21\; \div \;1\; = \;21\), \(21\; \div \;7\; = \;3\) et \(21\; \div \;21\; = \;1\). Les élèves pourraient constater que tout nombre naturel a au moins 2 diviseurs, soit le nombre lui-même et le nombre 1.
Puisque la multiplication et la division sont des opérations inverses, il est possible d’établir des relations entre les concepts de multiple, de facteur, de dividende, de diviseur et de quotient.
Par exemple, tout facteur d’un nombre est aussi un diviseur de ce nombre (4 est à la fois un facteur et un diviseur de 28). Ainsi, les relations entre les nombres peuvent être exprimées différemment selon l’analyse que l’on fait d’une situation donnée. Les élèves pourraient notamment dire que 8 est un multiple de 4, que 4 est un facteur de 8, que 8 est divisible par 4 ou que 4 est un diviseur de 8.
Elles et ils pourraient aussi reconnaître que le nombre 24 est un multiple de l’ensemble des nombres {1, 2, 3, 4, 6, 8, 12 et 24} et que ces nombres sont ses facteurs ou ses diviseurs.
Certaines situations impliquent la recherche d’un diviseur commun à 2 nombres. Cette recherche, tout comme la recherche de multiples communs, devrait être effectuée dans un contexte de résolution de problèmes.
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 56-58.
Le plus grand facteur commun (PGFC)
L’élève utilise les stratégies pour trouver le plus grand facteur commun afin d’être efficace lors de la simplification d’une fraction.
Exemple
Simplifie la fraction \(\frac{{36}}{{54}}\).
Stratégie :
Pour simplifier cette fraction, l’élève trouve le PGFC de 36 et 54.
Elle ou il trouve toutes les combinaisons de facteurs qui donnent 36 et 54. Lui suggérer de commencer avec 1.
Par exemple, l’élève peut se poser la question suivante : 1 fois quel nombre donne 36 ou 36 divisé par 1 donne quel nombre? Continuer avec 2 et ainsi de suite.
 Image
Voici deux listes de multiplications. Première liste : facteurs de 36. Une fois 36 égale 36. Deux fois dix-huit égale
36. Trois fois douze égale 36.
Quatre fois neuf égale 36. Et six fois six égale 36. Deuxième liste : Facteurs de 54. Une fois 54 égale 54. Deux fois
27 égale 54. Trois fois 18 égale 54. Et six fois neuf égale 54.
Image
Voici deux listes de multiplications. Première liste : facteurs de 36. Une fois 36 égale 36. Deux fois dix-huit égale
36. Trois fois douze égale 36.
Quatre fois neuf égale 36. Et six fois six égale 36. Deuxième liste : Facteurs de 54. Une fois 54 égale 54. Deux fois
27 égale 54. Trois fois 18 égale 54. Et six fois neuf égale 54.
Les facteurs de 36 sont 1, 2, 3, 4, 6, 9, 12, 18, 36.
Les facteurs de 54 sont 1, 2, 3, 6, 9, 18, 27, 54.
Par conséquent, l’élève choisit le plus grand facteur des 2 listes.
Le PGFC est 18.
L’élève peut maintenant simplifier la fraction à sa forme irréductible.
\(\frac{{36\; \div \;18}}{{54\; \div \;18}}\; = \;\frac{2}{3}\)
L’élève factorise le numérateur et le dénominateur à partir du PGFC.
Exemple
M. Theis a 36 stylos rouges et 120 stylos bleus. Il veut répartir tous ces stylos en paquets de stylos rouges et en paquets de stylos bleus. Il veut aussi faire en sorte que le nombre de stylos dans les paquets de stylos bleus soit le même que dans les paquets de stylos rouges.
a) Combien de stylos peut-il mettre dans chaque paquet?
b) Quel est le plus grand nombre de stylos qu’il peut mettre dans chaque paquet?
Pour résoudre ce problème, les élèves peuvent dresser la liste des diviseurs possibles de 36 et de 120.
 Image Voici deux listes de divisions. Première liste : diviseurs de 36. 36 divisé par un égale 36. 36 divisé par deux
égale 18. 36 divisé par trois égale
douze. 36 divisé par quatre égale neuf. 36 divisé par six égale six. Et 36 divisé par douze égale trois. Deuxième
liste : diviseurs de 120. 120 divisé par un égale 120. 120 divisé par deux égale 60. 120 divisé par trois
égale 40. 120 divisé par quatre égale 30. 120 divisé par six égale 20. Et 120 divisé par 12 égale dix.
Image Voici deux listes de divisions. Première liste : diviseurs de 36. 36 divisé par un égale 36. 36 divisé par deux
égale 18. 36 divisé par trois égale
douze. 36 divisé par quatre égale neuf. 36 divisé par six égale six. Et 36 divisé par douze égale trois. Deuxième
liste : diviseurs de 120. 120 divisé par un égale 120. 120 divisé par deux égale 60. 120 divisé par trois
égale 40. 120 divisé par quatre égale 30. 120 divisé par six égale 20. Et 120 divisé par 12 égale dix.
En comparant les listes et en statuant que 1 stylo ne constitue pas un « paquet », elles et ils pourront constater que M. Theis peut faire des paquets de 2, de 3, de 4, de 6 ou de 12 stylos et que 12 est le plus grand nombre de stylos qu’il peut mettre dans un paquet.
12 est donc le plus grand facteur commun (PGFC).
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 58.
Le plus petit commun multiple (PPCM)
L’élève doit connaître le plus petit commun multiple (PPCM) afin d’additionner et soustraire des fractions sans dénominateur commun. L’élève trouve des fractions équivalentes afin de pouvoir effectuer ses calculs. Dans ce cas, le plus petit commun multiple est déterminé pour tous les dénominateurs.
Exemple
\(\frac{5}{{12}}\; + \;\frac{1}{{18}}\; = \;?\)
Stratégies possibles :
L’élève trouve le PPCM de 12 et 18 afin d’avoir un dénominateur commun.
- L’élève trouve les multiples de 12 et 18. Elle ou il s’arrête lorsque le 1er multiple commun est identifié.

Donc, le PPCM de 12 et 18 est 36.
- L’élève trouve tous les facteurs premiers des 2 nombres à l’aide d’arbres de facteurs.
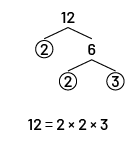 Image Le nombre douze se relie par deux branches au chiffre
deux, qui est encerclé, et au chiffre six. Le chiffre six se relie par deux branches aux chiffres deux et trois,
tous deux encerclées. En dessous, il est écrit : douze égale deux fois deux fois trois.
Image Le nombre douze se relie par deux branches au chiffre
deux, qui est encerclé, et au chiffre six. Le chiffre six se relie par deux branches aux chiffres deux et trois,
tous deux encerclées. En dessous, il est écrit : douze égale deux fois deux fois trois. 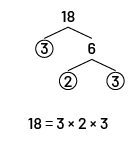 Image
Le nombre 18 se relie par deux branches au chiffre trois, qui est encerclé, et au chiffre six. Le chiffre six se
relie par deux branches aux chiffres deux et trois, tous deux encerclées. En dessous, il est écrit : 18 égale trois
fois deux fois trois.
Image
Le nombre 18 se relie par deux branches au chiffre trois, qui est encerclé, et au chiffre six. Le chiffre six se
relie par deux branches aux chiffres deux et trois, tous deux encerclées. En dessous, il est écrit : 18 égale trois
fois deux fois trois. Pour trouver le PPCM, l’élève ressort les facteurs premiers qui sont communs aux deux nombres (biffés ici-bas). Par la suite, il identifie les facteurs premiers restants.
Facteurs premiers communs aux 2 nombres : 2 et 3
 Image
Dans la séquence « douze deux-points deux, deux, trois », le premier deux et le trois sont raturés en rouge. Dans la
séquence « 18 deux-points deux, trois, trois », le deux et le premier trois sont raturés en rouge.
Image
Dans la séquence « douze deux-points deux, deux, trois », le premier deux et le trois sont raturés en rouge. Dans la
séquence « 18 deux-points deux, trois, trois », le deux et le premier trois sont raturés en rouge.
Facteurs premiers restant aux 2 nombres : 2 et 3
Donc, le PPCM est le produit de la multiplication des facteurs premiers communs par les facteurs premiers restants.
PPCM : \((2\; \times \;3)\; \times \;(2\; \times \;3)\; = \;36\)
L’élève peut maintenant poursuivre avec l’addition des 2 fractions avec un dénominateur commun de 36.
\(\frac{5}{{12}}\; + \;\frac{1}{{18}}\; = \;\frac{{5\; \times \;3}}{{12\; \times \;3}}\; + \;\frac{{1\; \times \;2}}{{18\; \times \;2}}\; = \;\frac{{15}}{{36}}\; + \;\frac{2}{{36}}\; = \;\frac{{17}}{{36}}\)
Connaissance : multiple
Nombre naturel correspondant au produit de ce nombre par un autre nombre naturel. Par exemple, certains multiples de 4 sont 4, 8, 12, 16 et 20 (\(4\; \times \;1\), \(4\; \times \;2\), \(4\; \times \;3\), \(4\; \times \;4\), \(4\; \times \;5\)).
Connaissance : plus petit commun multiple (PPCM)
Le plus petit de tous les multiples entiers communs à 2 ou à plusieurs nombres entiers. Par exemple, le plus petit commun multiple (PPCM) des nombres 10 et 12 est 60.
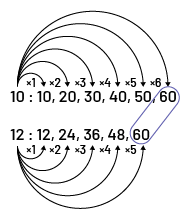 Image Deux séquences sont présentées. Première séquence : dix deux-points dix, 20, 30, 40, 50, 60. Une flèche relie
le premier dix au deuxième dix en
indiquant fois un. Une flèche relie le premier dix à 20 en indiquant fois deux. Une flèche relie le premier dix à 30
en indiquant fois trois. Une flèche relie le premier dix à 40 en indiquant fois quatre. Une flèche relie le premier
dix à 50 en indiquant fois cinq. Et une flèche relie le premier dix à 60 en indiquant fois six. Deuxième séquence :
douze deux-points douze, 24, 36, 48, 60. Une flèche relie le premier douze au deuxième douze en
indiquant fois un. Une flèche relie le premier douze à 24 en indiquant fois deux. Une flèche relie le premier douze
à 36 en indiquant fois trois. Une flèche relie le premier douze à 48 en indiquant fois quatre. Et une flèche relie
le premier douze à 60 en indiquant fois cinq. Les deux nombres 60 sont encerclés ensemble.
Image Deux séquences sont présentées. Première séquence : dix deux-points dix, 20, 30, 40, 50, 60. Une flèche relie
le premier dix au deuxième dix en
indiquant fois un. Une flèche relie le premier dix à 20 en indiquant fois deux. Une flèche relie le premier dix à 30
en indiquant fois trois. Une flèche relie le premier dix à 40 en indiquant fois quatre. Une flèche relie le premier
dix à 50 en indiquant fois cinq. Et une flèche relie le premier dix à 60 en indiquant fois six. Deuxième séquence :
douze deux-points douze, 24, 36, 48, 60. Une flèche relie le premier douze au deuxième douze en
indiquant fois un. Une flèche relie le premier douze à 24 en indiquant fois deux. Une flèche relie le premier douze
à 36 en indiquant fois trois. Une flèche relie le premier douze à 48 en indiquant fois quatre. Et une flèche relie
le premier douze à 60 en indiquant fois cinq. Les deux nombres 60 sont encerclés ensemble.
Connaissance : facteur
Nom donné à un nombre entier qui intervient dans une multiplication.
Exemple
Les facteurs de 12 sont 1, 2, 3, 4, 6 et 12.
Note : Généralement, les facteurs d’un nombre sont des nombres entiers positifs. Puisque la multiplication et la division sont des opérations inverses, il est possible d’établir des relations entre les concepts de multiple, de facteur, de dividende, de diviseur et de quotient. Par exemple, tout facteur d’un nombre est aussi un diviseur de ce nombre (4 est à la fois un facteur et un diviseur de 28).
Connaissance : facteur premier
Facteur qui est un nombre premier dans la décomposition en facteurs d’un nombre. Par exemple, \(90\; = \;2\; \times \;3\; \times \;3\; \times \;5\).
Les facteurs premiers du nombre 90 sont 2, 3 et 5.
Connaissance : arbre de facteurs
Schéma servant à dresser une liste de facteurs premiers.
Exemple :
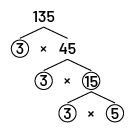 Image Le nombre 135 se relie par deux branches à trois, qui est
encerclé, et à 45. 45 se relie par deux branches à trois et à 15, tous deux encerclés. Quinze se relie par deux
branches à trois et à cinq, tous deux encerclés.
Image Le nombre 135 se relie par deux branches à trois, qui est
encerclé, et à 45. 45 se relie par deux branches à trois et à 15, tous deux encerclés. Quinze se relie par deux
branches à trois et à cinq, tous deux encerclés.
Connaissance : diviseur
Nom donné à un nombre entier qui en divise un autre.
Exemple : Les diviseurs de 6 sont 1, 2, 3 et 6.
Note : Généralement, les diviseurs d’un nombre sont des nombres entiers positifs. Puisque la multiplication et la division sont des opérations inverses, il est possible d’établir des relations entre les concepts de multiple, de facteur, de dividende, de diviseur et de quotient. Par exemple, tout facteur d’un nombre est aussi un diviseur de ce nombre (4 est à la fois un facteur et un diviseur de 28).
Source : En avant les maths! 7e année, CM, Nombres, p. 2.
