À vue d'oeil...

B2.9 Multiplier et diviser des nombres décimaux par d’autres nombres décimaux, dans divers contextes.

Habileté : multiplier et diviser des nombres décimaux par d’autres nombres décimaux, dans divers contextes

---

Multiplication

Les élèves du cycle moyen ont déjà une expérience du concept de multiplication et comprennent que la multiplication de nombres naturels a pour effet de générer un produit supérieur aux quantités en cause, sauf dans les situations de multiplications par 1 et par 0.

En 5^e année, elles et ils sont alors souvent surpris de constater qu’une multiplication dont l’un des facteurs est un nombre décimal inférieur à 1 donne un produit inférieur à l’autre facteur (par exemple, \(10\; \times \;0,5\; = \;5\); \(20\; \times \;0,1\; = \;2\)).

Ces résultats sont surprenants pour quiconque ne traite pas les nombres en contexte ou n’a pas acquis une compréhension de la multiplication lui permettant d’expliquer de tels résultats.

Exemple

Si les élèves doivent déterminer la distance parcourue par un lapin qui fait 8 bonds de 0,5 m, elles et ils sont confrontés à une multiplication qui donne un produit inférieur au facteur 8, car \(0,5\; \times \;8\; = \;4\) (le lapin a fait un bond de 0,5 m 8 fois). Pour évaluer l’expression \(0,5\; \times \;8\), on peut utiliser une droite numérique et représenter les 8 bonds. On obtient une distance totale de 4 m.

Image Une droite numérique est graduée de zéro à cinq par marques d’intervalles de zéro virgule cinq. Des flèches relient chaque marque d’intervalle à la suivante, de zéro à quatre, en indiquant zéro virgule cinq à chaque reprise.

Même s’il peut paraître surprenant que le produit soit inférieur au facteur 8, le contexte permet aux élèves d’en saisir la raison. Les élèves acquièrent alors une meilleure compréhension de la multiplication qui tient compte de telles situations.

Source : Guide d'enseignement efficace des mathématiques de la 4^e à la 6^e année, p. 79.

En général, il existe 2 façons d’interpréter une multiplication écrite de façon symbolique, par exemple \(3\; \times \;4\). On peut l’interpréter comme étant 3 fois le nombre 4, ce qui est équivalent à 3 groupes de 4, ou comme étant le nombre 3 multiplié par 4, ce qui est équivalent à 4 groupes de 3. Selon Baruk (1995, p. 737), une expression comme le nombre 3 multiplié par 4 est « lourde et peu en accord avec l’expression naturelle dans la langue d’une quantité qui se répète ». Dans ce document, l’expression \(3\; \times \;4\) sera interprétée comme étant 3 fois le nombre 4 ou 3 groupes de 4 afin de respecter le sens le plus naturel.

Si les élèves ont bien saisi que \(3\; \times \;4\) signifie 3 groupes de 4, ils pourront comprendre le sens de \(8\; \times \;0,5\), soit 8 groupes de 0,5 comme le montre l’illustration suivante dans laquelle une planchette représente l’unité.

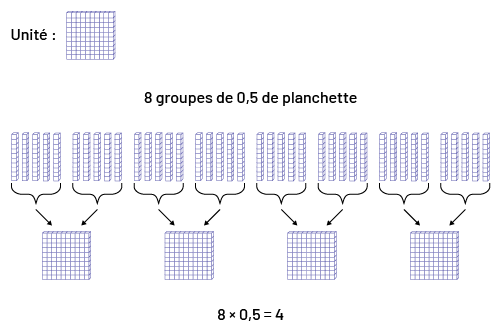Image Dans ce schéma, un carré représente une unité. Huit groupes de zéro virgule cinq de planchette sont alignés côte à côte. Sous ceux-ci, il y a quatre carrés. Les deux premiers groupes de demi-planchette pointent vers le premier carré à l’aide de flèches. Les troisième et quatrième groupes de demi-planchette pointent vers le deuxième carré. Les cinquième et sixième groupes de demi-planchette pointent vers le troisième carré. Et les septième et huitième groupes de demi-planchette pointent vers le quatrième carré. Sous les carrés, il est écrit : huit fois zéro virgule cinq égale quatre.

Lorsqu’on multiplie un nombre naturel par 0,1 la valeur devient 10 fois plus petite, qui est la même chose que diviser par 10.

Lorsqu’on multiplie un nombre naturel par 0,01, la valeur devient 100 fois plus petite, qui est la même chose que diviser par 100.

• Multiplication effectuée à l’aide du tableau de valeur de position

\(23\; \times \;0,1\; = \;2,3\)

Je visualise un déplacement de 1 colonne vers la droite dans le tableau de valeur de position.

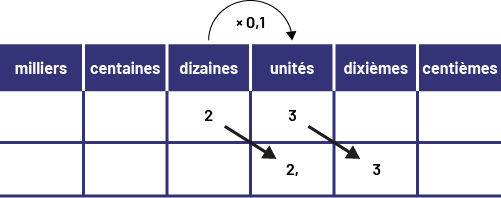Image Voici un tableau dont chaque colonne présente deux cases. Les colonnes vont comme suit : milliers, centaines, dizaines, unités, dixièmes, centièmes. Dans la première case des dizaines, il y a le chiffre deux, relié par une flèche à la deuxième case des unités laquelle contient aussi le chiffre deux. Dans la première case des unités, il y a le chiffre trois, relié par une flèche à la deuxième case des dixièmes laquelle contient aussi le chiffre trois. Toutes les autres cases sont vides. Au-dessus de la colonne unités, il est écrit fois zéro virgule un.

\(23\; \times \;0,01\; = \;0,23\)

Je visualise un déplacement de 2 colonnes vers la droite dans le tableau de valeur de position.

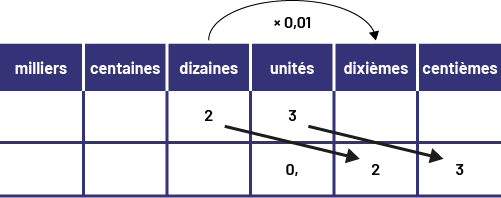Image Voici un tableau dont chaque colonne présente deux cases. Les colonnes vont comme suit : milliers, centaines, dizaines, unités, dixièmes, centièmes. Dans la première case des dizaines, il y a le chiffre deux, relié par une flèche à la deuxième case des dixièmes, qui contient le chiffre deux. Dans la première case des unités, il y a le chiffre trois, relié par une flèche à la deuxième case des centièmes, qui contient le chiffre trois. Dans la deuxième case des unités, il y a un zéro avec une virgule. Toutes les autres cases sont vides. Au-dessus du tableau, entre unités et dixièmes, il est écrit fois zéro virgule zéro un.

Au départ, il est très important de comprendre un élément du sens du nombre, soit la relation d’ordre de grandeur entre 2 nombres composés des mêmes chiffres dans le même ordre. Cette relation peut être reconnue en observant la position de la virgule dans les nombres.

Exemple

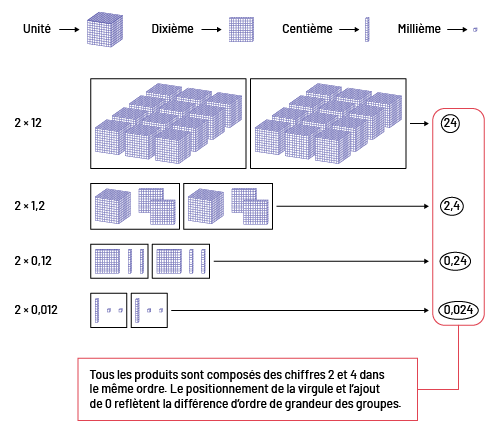
Cette compréhension rend inutile l’apprentissage de règles comme « lorsqu’on multiple par 10, on pousse la virgule d’une place vers la droite ». Les élèves peuvent plutôt analyser la situation d’une multiplication dont un des facteurs est un nombre décimal. Par exemple, elles et ils peuvent découvrir que les produits de \(2 \times 12\); de \(2 \times 1,2\); de \(2 \times 0,12\) et de \(2 \times 0,012\) sont apparentés. Dans ces expressions, les chiffres 1 et 2 paraissent ensemble dans le même ordre dans un des facteurs. De même, les chiffres 2 et 4 paraissent ensemble dans le même ordre dans le produit. Les élèves pourraient expliquer cette relation de la façon suivante :

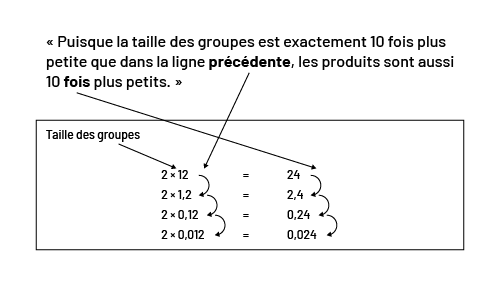Image Dans un grand rectangle, il est écrit « Taille des groupes », qui pointe avec une flèche vers la première équation d’une série de quatre. Première équation : deux fois douze égale 24. Deuxième équation : deux fois un virgule deux égale deux virgule quatre. Troisième équation : deux fois zéro virgule douze égale zéro virgule 24. Quatrième équation : deux fois zéro virgule zéro douze égale zéro virgule zéro quatre. Chaque multiplicateur se lie au multiplicateur suivant par une flèche, et chaque produit se lie au produit suivant par une flèche. Au-dessus du rectangle, il est écrit : « Puisque la taille des groupes est exactement dix fois plus petite que dans la ligne précédente, les produits sont aussi dix fois plus petits. ». Les mots « précédente » et « fois » sont en caractères gras. Le premier se lie par une flèche vers les multiplicateurs et le deuxième se lie par une flèche aux produits.

Le tableau suivant démontre cette même relation à l’aide de représentations concrètes.

Image Légende de l’illustration : un gros cube équivaut à une unité, une grille équivaut à un dixième, un bâtonnet équivaut à un centième et un petit cube équivaut à un millième. Quatre multiplications sont illustrées l’une sous l’autre. La multiplication deux fois douze est illustrée par deux ensembles de douze gros cubes. À droite, une flèche pointe vers le nombre 24. La multiplication deux fois un virgule deux est illustrée par deux ensembles d’un gros cube et de deux grilles. À droite, une flèche pointe vers le chiffre deux virgule quatre. La multiplication deux fois zéro virgule douze est illustrée par deux ensembles d’une grille et de deux bâtonnets. À droite, une flèche pointe vers le chiffre zéro virgule 24. La multiplication deux fois zéro virgule zéro douze est illustrée par deux ensembles d’un bâtonnet et de deux petits cubes. À droite, une flèche pointe vers le chiffre zéro virgule zéro zéro 24. Tous les produits sont encerclés ensemble et se lient au texte suivant : Tous les produits sont composés des chiffres deux et quatre dans le même ordre. Le positionnement de la virgule et l’ajout de zéro reflètent la différence d’ordre de grandeur des groupes

Ainsi, lorsque les élèves saisissent bien la relation entre les facteurs 12, 1,2, 0,12 et 0,012, soit que chacun est 10 fois plus petit que le précédent, et l’effet de cette relation sur le produit, elles et ils comprennent pourquoi il est possible de multiplier les nombres décimaux comme s’il s’agissait de nombres naturels, puis de positionner la virgule en se basant sur l’estimation et sa connaissance de l’ordre de grandeur. Comme le démontrent les exemples ci-dessus, c’est en développant et en utilisant leur sens du nombre que les élèves apprennent à déterminer la position de la virgule dans le produit et non en apprenant une règle de plus. Voici des exemples de l’utilisation de l’estimation pour déterminer la position de la virgule dans un produit.

Image Un tableau possède trois colonnes : Opération, Estimation, Produit. Dans la colonne opération il est écrit : « cinq fois 25 », avec une flèche pointant à droite, et « cinq fois deux virgule cinq », avec une flèche pointant à droite. Dans la colonne Estimation, vis-à-vis la première flèche, il est écrit : « cinq groupes de 25, donc 125 »; et vis-à-vis la deuxième flèche, il est écrit : « cinq groupes de deux, soit environ dix ». Dans la colonne estimation, il est écrit, entre parenthèses : « puisque les chiffres un, deux et cinq se retrouvent dans cet ordre dans le produit. » En dessous, il y a une flèche pointant à droite vers le nombre 125. Sous ceci, il y a une flèche pointant à droite vers le nombre douze virgule cinq.

Source : Guide d'enseignement efficace des mathématiques de la 4^e à la 6^e année, p. 81-83.

En 6^e année, l’élève multiplie un nombre naturel à 3 chiffres par un nombre décimal jusqu’aux dixièmes.

Dans l’enseignement traditionnel de la multiplication sur les nombres décimaux, on fait apprendre un algorithme. Par exemple, pour effectuer \(0,1\; \times \;125\), on procède d’abord comme pour des entiers :

\(\begin{align} 125 \;\;\;\;\;\; \\\underline { \times \;\;0,1} \\125 \;\;\;\;\;\;\end{align}\)

Ensuite, on compte le nombre de décimales dans les 2 facteurs (1 dans le présent exemple) et on place la virgule dans le produit afin qu’il ait le même nombre de décimales. On obtient alors :

\(\begin{align} 125 \;\;\;\;\;\; \\\underline { \times \;\;0,1} \\12,5\;\;\;\;\;\end{align}\)

Pour les élèves, il s’agit d’apprendre une règle de plus, ce qui renforce leur impression qu’apprendre les mathématiques consiste à apprendre à obéir à une multitude de règles. Or, l’apprentissage de cette règle a perdu de son importance avec l’avènement de la calculatrice. Il est plus important pour les élèves de bien intégrer les particularités de la multiplication de nombres décimaux à leurs connaissances de la multiplication de nombres naturels et d’accroître leur sens du nombre et leur sens des opérations de manière à prévoir l’ordre de grandeur du produit de 2 nombres donnés.

Source : Guide d'enseignement efficace des mathématiques de la 4^e à la 6^e année, p. 80-81.

Lorsque les élèves représentent la multiplication d’un nombre naturel par un nombre décimal de façon concrète ou semi-concrète (par exemple, à l’aide de matériel de base 10, d’une droite numérique, d’une disposition rectangulaire), ils saisissent mieux le sens de la multiplication. Les stratégies pour multiplier les nombres décimaux sont essentiellement les mêmes que celles utilisées pour multiplier les nombres naturels. Voici différentes stratégies de multiplication d’un nombre décimal par un nombre naturel.

Exemple

\(1,3\; \times \;300\)

Afin d’estimer le produit, il est possible de raisonner comme suit : 1,3 se situe entre 1 et 2; donc \(1,3\; \times \;300\), c’est entre \(300\;\;\;\;\;(300\; \times \;1)\) et \(600\;\;\;\;\;(300\; \times \;2)\). Il y a un peu plus qu’un groupe de 300.

• Multiplication à l’aide de matériel de base 10

Je décompose 1,3 en \(1\; + \;0,3\). Je multiplie \(1\; \times \;300\).

Ensuite, je décompose 0,3 en \(0,1\; + \;0,1\; + \;0,1\) puisque je sais que 0,1 de 300 est 30. Alors, j’additionne \(30\; + \;30\; + \;30\; = \;90\).

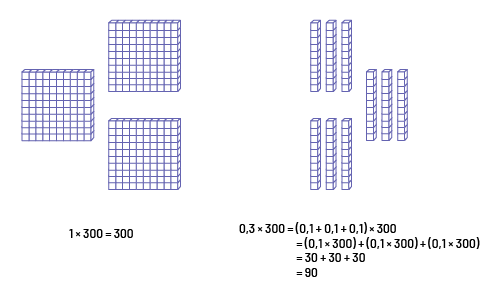Image Deux ensembles de cubes sont présentés côte à côte. Le premier ensemble se constitue de trois grilles de cent cubes unités. En dessous il est écrit : une fois 300 égale 300. Le deuxième ensemble se constitue de trois ensembles de trois bâtonnets de dix unités. En dessous, il est écrit : zéro virgule trois fois 300 égale parenthèse ouvrante zéro virgule un plus zéro virgule un plus zéro virgule un parenthèse fermante fois 300, égale parenthèse ouvrante zéro virgule un fois 300 parenthèse fermante plus zéro virgule un fois 300 parenthèse fermante plus parenthèse ouvrante zéro virgule un parenthèse fermante, égale 30 plus 30 plus 30, égale 90.

• Multiplication à l’aide d’une disposition rectangulaire

J’ai décomposé les 2 facteurs, 1,3 en \(1\; + \;0,3\) pour les rangées et 300 en \(100\; + \;100\; + \;100\) pour les colonnes.

Image Un rectangle est divisé en six parties. Dans le sens de la largeur, la partie du haut mesure un virgule zéro et la partie du bas mesure zéro virgule trois. Dans le sens de la longueur, les trois parties mesurent chacune cent. Dans chacune des trois parties du haut, il est écrit cent; tandis que dans chacune des trois parties du bas, il est écrit trente. À droite du rectangle, il est écrit : 300 plus 90 égale 390.

J’ai multiplié chaque centaine par un (\(100\; + \;100\; + \;100\)).

Ensuite, j’ai multiplié chaque centaine par 0,3 (\(30\; + \;30\; + \;30\)).

\(300\; + \;90\; = \;390\).

• Multiplication à l’aide d’une droite numérique
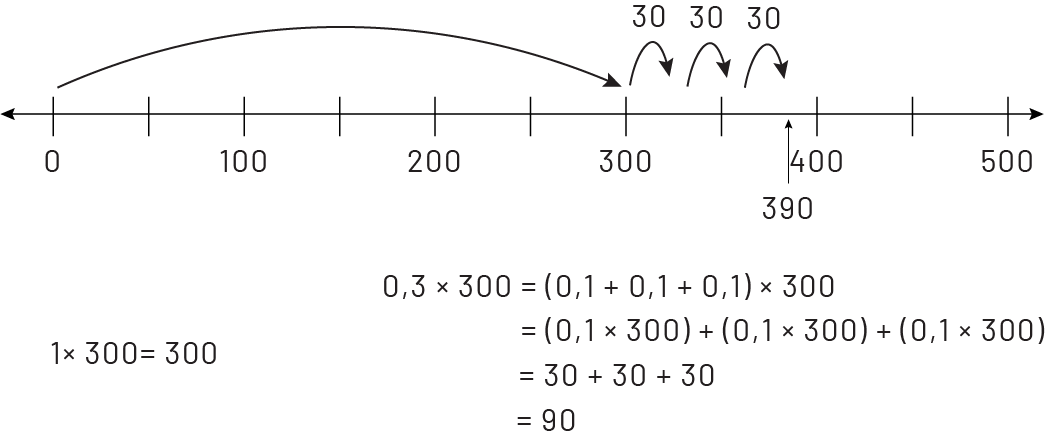Image Une double droite numérique est graduée de zéro à 500, par intervalles de cent, avec des marques d’intervalles de cinquante. Une flèche relie zéro à 300. Une flèche part de 300 et s’arrête entre 300 et 350 en indiquant 30. Une flèche part de cet endroit et se rend légèrement passé 350 en indiquant 30. Une flèche part de cet endroit et se rend à 390, le nombre a été ajouté, en indiquant 30.

• Multiplication à l’aide d’un algorithme personnel

Exemple

Les calculs sont effectués en partant de la gauche et selon la valeur de position.

• Multiplication à l’aide de l’algorithme usuel de la multiplication

Note : Dans le cas de l’algorithme usuel, il est important que les élèves n’apprennent pas une procédure par cœur, mais qu’elles et ils comprennent chacune des étapes de la procédure et qu’ils puissent l’expliquer et l’associer à une représentation concrète ou semi-concrète.

Source : Guide d'enseignement efficace des mathématiques de la 4^e à la 6^e année, p. 104-107.

L’élève de 7^e année multiplie un nombre décimal par un autre nombre décimal. Au fil de son apprentissage, elle ou il devient plus sélectif dans le choix de sa stratégie pour résoudre un problème, représente ses calculs de façon plus structurée et adopte des démarches qui sont de plus en plus efficaces.

Puisque les élèves ont déjà développé et utilisé plusieurs algorithmes personnels comprenant des nombres naturels, elles et ils pourront établir des liens entre ces stratégies et celles utilisées pour effectuer des opérations sur les nombres décimaux. Ces algorithmes permettront aux élèves de donner un sens à la multiplication et la division.

Source : Les mathématiques… un peu, beaucoup, à la folie!, Guide pédagogique, Numération et Sens du nombre/Mesure, 8^e année, Module 2, Série 1, p. 16-17.

Exemple

\(16,5\; \times \;1,5\)

• Multiplication effectuée à l’aide de la disposition rectangulaire

Je me sers de la distributivité afin de décomposer 16,5 et 1,5 en (\(16\; + \;0,5\)) et (\(1\; + \;0,5\)). Je divise le rectangle en rangées et en colonnes.

Image Un rectangle est divisé par une ligne verticale près de son côté droit et par une ligne horizontale près de sa base. Le long côté de sa longueur mesure 16 et le court côté mesure zéro virgule cinq. Le long côté de sa largeur mesure un et le court côté mesure zéro virgule cinq. À l’intérieur, le côté en haut à gauche a une superficie de 16, le côté en haut à droite a une superficie de zéro virgule cinq, le côté gauche en bas a une superficie de huit et le côté droit en bas a une superficie de zéro virgule 25.

Pour trouver le produit, j’additionne tous les produits partiels.

\(16\; + \;8\; + \;0,5\; + \;0,25\; = \;24,75\)

\(16,5\; \times \;1,5\; = \;24,75\)

• Multiplication effectuée à l’aide de l’algorithme usuel

Notons que les algorithmes usuels de multiplication pour les nombres naturels peuvent s’appliquer aux nombres décimaux. Comme pour les nombres naturels, ces algorithmes additionnent des produits partiels pour créer un total.

Estimation

\(\begin{array}{l}{\rm{1}}{\rm{,5 \ est \ entre \ 1 \ et \ 2}}\\16,5\; \times \;1,5\;\;{\rm{est \ entre \ 16 \ et \ 32}}{\rm{, \ puisque \ 16}}\; \times \;{\rm{1}}\;{\rm{ = }}\;{\rm{16 \ et \ 16}}\; \times {\rm{2}}\;{\rm{ = }}\;{\rm{32}}{\rm{.}}\end{array}\)

Une « bonne » estimation aide à vérifier la vraisemblance du produit (surtout au niveau du placement de la virgule).

Image Deux colonnes de calculs sont présentées côte à côte. La première colonne s’intitule « Comment l’écrire ». Le calcul est disposé de façon verticale, les entiers sous les entiers, les décimaux sous les décimaux, le tout bien vis-à-vis. Le calcul est : 16 virgule cinq fois un virgule cinq égale zéro virgule 25 plus trois plus cinq plus zéro virgule cinq plus six plus dix égale 24 virgule 75. La deuxième colonne s’intitule « Ce qui se passe ». Chaque multiplication est écrite l’une sous l’autre : à zéro virgule cinq fois zéro virgule cinq; à zéro virgule cinq fois six; à zéro virgule cinq fois dix; à une fois zéro virgule cinq; à une fois six; à une fois dix.

• Multiplication effectuée à l’aide de la relocalisation

Une stratégie pour multiplier les nombres décimaux est de les décomposer comme un produit de nombres naturels multipliés par 10, 100 ou 1 000, afin d’obtenir des nombres naturels. Lorsque le produit est obtenu, il faut diviser par le même nombre.

Je multiplie 16,5 par 10 et 1,5 par 10 afin de relocaliser la virgule.

\((16,5\; \times \;10)\; \times \;(1,5\; \times \;10)\; = \;165\; \times \;15\)

Je poursuis avec la multiplication les nombres naturels \(165\; \times \;15\).

\(\begin{array}{r} 165\\\underline { \times 15} \\\ 25\\\ 300\\\ 500\\\ 50\\\ 600 \;\\\underline { + 1\;000} \\\ 2\;475\end{array}\)

Lorsque le produit des nombres naturels est obtenu, pour maintenir l’équivalence, il faut diviser le produit par \(100\;\;\;\;\;\;(10\; \times \;10)\) puisqu’on a multiplié chaque facteur par 10 (stratégie de compensation).

\(2\;475\; \div \;100\; = \;24,75\)

Donc, \(16,5\; \times \;1,5\; = \;24,75\)

Note : Au départ, si l’élève a estimé que le nombre est entre 16 et 32, elle ou il peut déduire que la virgule est placée entre le 4 et le 7.

• Multiplication effectuée à l’aide d’une multiplication équivalente

Une stratégie pour multiplier les nombres décimaux est de les décomposer comme un produit de nombres naturels multipliés par des dixièmes, des centièmes ou des millièmes, afin d’obtenir des nombres naturels.

Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1^re à la 8^e année, 2020, Ministère de l’Éducation de l’Ontario.

\(\begin{align}16,5 \times \;1,5\; &= \;165\; \times \;0,1\; \times 15\; \times \;0,1\\ &= \;165\; \times \;15\; \times \;0,01\\ &= \;(165\; \times \;10)\; + \;(165\; \times \;5)\; \times \;0,01\\ &= \;(1\;650\; + \;825)\; \times \;0,01\\ &= \;2\;475\; \times \;0,01\\ &= \;24,75\end{align}\)

Division

Au cours de leur apprentissage, les élèves ont appris qu’une division comme \(12\; \div \;3\) s’effectue selon un contexte où l’on crée des groupes de 3 éléments (sens de groupement) ou selon celui où l’on crée 3 groupes égaux (sens de partage). Ces 2 contextes existent aussi en présence d’une division d’un nombre décimal par un nombre naturel.

Source : Guide d'enseignement efficace des mathématiques de la 4^e à la 6^e année, p. 83.

Cependant, en 6^e année, les élèves effectuent la division d’un nombre naturel par un nombre décimal. Lors de ce type de division, les contextes appellent en général à une division qui a le sens de groupement, la question étant : « Combien de dixièmes y a-t-il dans cette quantité? ».

Source : modifié du Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1^re à la 8^e année, 2020, Ministère de l’Éducation de l’Ontario.

Exemple

Un ruban mesurant 110 cm est coupé en morceau de 5,5 cm pour fabriquer des boucles. Combien de boucles peuvent être créées?

\(110\; \div \;5,5\; = \;?\)

Estimation

\(\begin{align}110\; \div \;5,5\; &\approx \;100\; \div \;5\\ &\approx \;20\end{align}\)

• Division effectuée à l’aide d’une multiplication

\(5,5\; \ \times \;?\; = \;110 \)

\(5,5\; \times \;20\; = \;110\)

20 boucles peuvent être créées.

• Division effectuée à l’aide d’une disposition rectangulaire

Image Un rectangle est traversé par une ligne horizontale juste au-dessus de sa base. Au-dessus du rectangle, il est écrit le nombre 20 encerclé en rouge. À l’intérieur, il est écrit cent. À droite, il est écrit 110 avec une accolade qui englobe toute sa largeur. En bas, il est écrit dix avec une flèche qui pointe vers la ligne horizontale. À gauche, entre la base et la ligne horizontale, il est écrit zéro virgule cinq. Et à gauche au-dessus de la ligne horizontale, il est écrit cinq.

Il est possible d’effectuer la division d’un nombre naturel par un nombre décimal en utilisant diverses stratégies, stratégies qui sont essentiellement les mêmes que celles utilisées dans les situations de divisions avec des nombres naturels. Cependant, il est important que les élèves interprètent correctement le résultat. Pour ce faire, elles et ils doivent se référer à l’estimation faite au préalable afin de s’assurer de l’ordre de grandeur du quotient. Elles et ils doivent aussi se référer à la situation-problème afin de s’assurer du sens à donner au quotient, à savoir que le résultat obtenu représente la taille ou le nombre de groupes. Les élèves doivent aussi comprendre et être en mesure d’expliquer la stratégie retenue pour effectuer l’opération.

Souvent, lorsque la division d’un nombre décimal représente le sens de groupement, l’opération n’est pas effectuée selon ce sens puisque représenter un raisonnement de groupement exige la création et l’interprétation d’une partie d’un groupe, ce qui rend la démarche plus difficile à saisir.

Source : Guide d'enseignement efficace des mathématiques de la 4^e à la 6^e année, p. 107-108.

Une stratégie pour diviser des nombres naturels par un nombre décimal consiste à créer une division équivalente utilisant des nombres naturels.

Source : modifié du Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1^re à la 8^e année, 2020, Ministère de l’Éducation de l’Ontario.

Exemple

Min lit un livre de 135 pages. Son objectif est de lire de livre dans 4,5 jours. Combien de pages doit-elle lire par jour afin d’atteindre son objectif?

Estimation

\(\begin{align}135\; \div \;4,5\; &\approx \;135\; \div \;5 \approx \;(100\; \div \;5)\; + \;(35\; \div \;5)\\ &\approx \;20\; + 7\\ &\approx \;27\end{align}\)

• Division effectuée à l’aide d’une division équivalente

Il faut diviser 135 pages par 4,5 jours. Une division équivalente utilisant des nombres naturels est 1 350 ÷ 45, puisque je multiplie chaque nombre par 10 pour éliminer la virgule.

\(\begin{align}135\; \times \;10\; &= \;1\;350\\4,5\; \times \;10\; &= \;45\end{align}\)

\(1\;350\; \div \;45\; = \;30\)

Alors \(135\; \div \;4,5\; = \;30\)

Min doit lire 30 pages par jour.

• Division effectuée à l’aide de la disposition rectangulaire

Image Un rectangle est traversé par une ligne horizontale juste au-dessus de sa base. Au-dessus du rectangle, il est écrit le nombre 30 encerclé en rouge. À l’intérieur, il est écrit 120. À droite, il est écrit 135 avec une accolade qui englobe toute sa largeur. En bas, il est écrit 15 avec une flèche qui pointe vers la ligne horizontale. À gauche, entre la base et la ligne horizontale, il est écrit zéro virgule cinq. Et à gauche au-dessus de la ligne horizontale, il est écrit quatre.

Le reste

Dans une division, le concept de reste survient lorsque le quotient n’est pas un nombre entier. Pour plusieurs élèves, le reste n’est qu’un nombre qui paraît dans la « recette » de la division (par exemple, \(178\; \div \;0,8\; = \;222\) reste 4).

Cependant, lorsque l’opération surgit d’un contexte, le reste doit être traité afin de pouvoir répondre adéquatement au problème. Ainsi, les élèves peuvent développer l’habileté à traiter le reste si elles ou s’ils sont en situation de résolution de problèmes. Voici plusieurs façons de traiter le reste :

• le reste est réparti équitablement et exprimé sous la forme d’un nombre décimal;
• le reste est réparti équitablement et exprimé sous la forme d’une fraction;
• le reste est réparti parmi les groupes;
• le reste entraîne la majoration du quotient de 1;
• le reste est la réponse.

Source : Guide d'enseignement efficace des mathématiques de la 4^e à la 6^e année, p. 86-87.

En 7^e année, les élèves effectuent la division d’un nombre décimal par un nombre décimal.

Exemple

La distance de la capitale provinciale, Toronto à la capitale nationale, Ottawa est de 450,5 km. Un chauffeur d’autobus a pris 4,75 heures pour parcourir ce trajet. Quelle est la vitesse approximative, en kilomètre-heure, de l’autobus?

Estimation

Ça a pris environ 5 h pour parcourir à peu près 450 km. Combien de groupes de 5 y a-t-il dans 450? (\(5\; \times \;?\; = \;450\))

J’estime que l’autobus voyage à une vitesse moyenne d’environ 90 (km/h).

• Division effectuée à l’aide d’une division équivalente

Comme la multiplication, la division avec les nombres décimaux peut se calculer comme celle faite avec des nombres naturels. Donc, j’effectue la division comme si le quotient et le diviseur sont des nombres naturels.

\(\begin{align}450,5\; \div \;4,75\; &= \;(450,5\; \times \;100)\; \div \;(4,75\; \times \;100)\\ &= \;45\;050\; \div \;475\end{align}\)

Note : Depuis le cycle moyen, l’élève explore et utilise des algorithmes personnels ainsi que des algorithmes usuels pour trouver le quotient.

*Pour trouver la vitesse moyenne, la distance est divisée par le temps du trajet.

• Division effectuée à l’aide de l’algorithme usuel

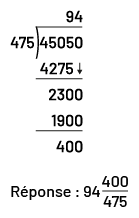Image Représentation d’un algorithme personnel d’un élève pour la division 45050 divisé par 475. Premièrement, peut-on diviser également les unités? Combien doit-on en placer dans chacun des 475 groupes? On doit placer 4 unités dans chaque groupe. J’inscris un 4 par-dessus le 0 des unités. Ceci me donne 1 900 et il reste 400. Il nous reste 400 unités qui ne peuvent être partagés en parts égales. Peut-on diviser également les unités? Combien doit-on en placer dans chacun des 475 groupes? On doit placer 4 unités dans chaque groupe. J’inscris un 4 par-dessus le 0 des unités. Ceci me donne 1 900 et il reste 400. Il nous reste 400 unités qui ne peuvent être partagés en parts égales. Peut-on diviser également les dizaines? Combien doit-on en placer dans chacun des 475 groupes? On doit placer 9 dizaines dans chaque groupe. J’inscris un 9 par-dessus le 5 des dizaines. Ceci me donne 4 275 et il reste 230. Si on échange 10 dizaines qui reste pour 1 unités, combien d’unités aurons-nous? Nous aurons 2 300 unités. Peut-on diviser également les dizaines? Combien doit-on en placer dans chacun des 475 groupes? On doit placer 9 dizaines dans chaque groupe. J’inscris un 9 par-dessus le 5 des dizaines. Ceci me donne 4 275 et il reste 230. Si on échange 10 dizaines qui reste pour 1 unités, combien d’unités aurons-nous? Nous aurons 2 300 unités. Peut-on diviser également les unités? Combien doit-on en placer dans chacun des 475 groupes. On doit placer 4 unités dans chaque groupe. J’inscris 4 par-dessus le 0 des unités. Ceci me donne 1900 et il reste 400. La réponse est donc 94 400/475.

Je peux donc dire que la vitesse approximative de l’autobus est de 94 km/h.

Généralisation

Le raisonnement utilisé ici haut permet de faire une généralisation concernant la division des nombres décimaux.

Par exemple, \(45,5\; \div \;0,45\) est équivalent à \(455\; \div \;4,5\) et \(4\;550\; \div \;45\).

Connaissance : nombre décimal

---

Nombre rationnel composé d’une partie entière (à gauche de la virgule) et d’une partie décimale (à droite de la virgule), soit une suite finie de chiffres.

Exemple

4,873; quatre et huit cent soixante-treize millièmes

Source : En avant, les maths! 7^e année, CM, Nombres, p. 2.