La vue d'ensemble

À vue d'oeil...

un remaniement des guides d'enseignement efficace en mathématiques

FrançaisEnglish

E1.1 Classer des solides et des figures planes selon un attribut à la fois et déterminer le critère de classement utilisé.

HABILETÉ : CLASSER DES SOLIDES ET DES FIGURES PLANES

Classer consiste à considérer ou à concevoir des classes dans lesquelles il est possible de grouper des objets, des figures planes ou des solides qui se différencient les uns des autres et à les placer en fonction de ces classes.

En 1re année, l’élève classe des solides et des figures planes.

Lorsque l’élève peut faire ressortir des ressemblances et des différences, elle ou il peut classer des objets, des figures planes ou des solides selon un attribut (par exemple, la grandeur, l’aire ou la couleur) en se servant par exemple de deux cerceaux ou de deux boîtes.

Plus tard, l’élève pourra classer des formes géométriques selon une propriété (par exemple, nature de la forme, nombre de sommets, nombre d’axes de symétrie).

Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 34.

Différentes façons de classer des solides

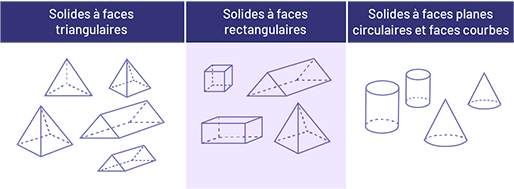
Tableau à 3 colonnes. La première colonne est nommée : « solides à faces triangulaires. » La deuxième colonne est nommée: « solides à faces rectangulaires. » La troisième colonne est nommée: « solides à faces planes circulaires et faces courbes. » Le tableau contient des exemples de chaque catégorie.

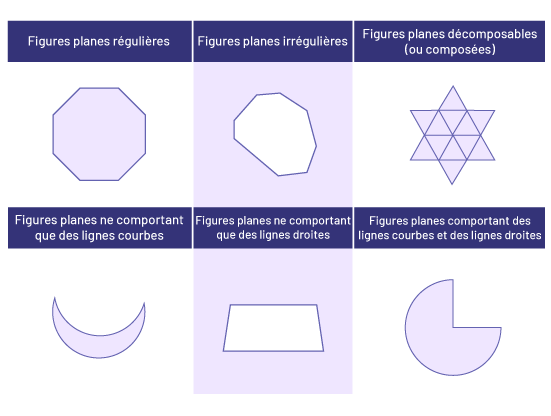
Types de figures planes à inclure dans une activité de classement 

Image tableau à 3 colonnes et 2 rangées. La première colonne, la première rangée: « figures planes régulières. » L’exemple est un octogone. La deuxième colonne, la première rangée: « figures planes irrégulières. » La troisième colonne, la première rangée: « figures planes décomposables (ou composées). » L’exemple est une étoile à 6 branches formées de 12 petits triangles. La première colonne, deuxième rangée: « figures planes ne comportant que lignes courbes. » L’exemple est un croissant de lune. La deuxième colonne, la deuxième rangée: « figures planes ne comprenant que des lignes droites. » L’exemple est un parallélépipède. La troisième colonne, deuxième rangée: « figures planes comportant des lignes courbes et des lignes droites. » L’exemple est un trois quart de cercle.

Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.

Lorsque l’élève a classé plusieurs formes selon un critère déjà choisi, le personnel enseignant lui demande de classer des figures planes ou des solides en choisissant son propre critère de classement.

Au moment de l’objectivation, le personnel enseignant demande à l’élève d’expliquer, par exemple, la propriété commune à toutes les formes de la même classe, afin de l’amener à distinguer les propriétés importantes de celles qui ne le sont pas dans l’identification d’une figure plane ou d’un solide.

Avec le temps, l’élève se rend compte que les familles de formes géométriques ont des propriétés communes (par exemple, tous les triangles ont trois côtés) et que les sous-ensembles ont des propriétés distinctes (par exemple, certains triangles ont deux côtés égaux).

Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 35.

CONNAISSANCE : PROPRIÉTÉ GÉOMÉTRIQUE

Une propriété géométrique est un attribut particulier à une figure plane ou à une famille de figures planes, à un solide ou à une famille de solides.

Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 32.

De la 1re à la 3e année, l’élève doit continuellement redéfinir l’image mentale qu’elle ou il se fait d’une figure plane ou d’un solide, car sa représentation mentale est souvent limitée à celle qu’on lui présente le plus souvent ou à une représentation stéréotypée. Une variété de représentations des formes géométriques aide l’élève à comprendre l’invariance des propriétés de la forme, peu importe le matériau, la taille, l’orientation, la perspective, etc. Par exemple, toute forme à deux dimensions ayant quatre côtés congrus et quatre côtés droits est un carré.

Il importe donc que, au cours d’activités dirigées de mathématiques, le personnel enseignant profite de l’occasion pour présenter une grande variété de représentations :

  • de formes géométriques;
  • de figures planes de toutes sortes, de taille et d’orientation différentes;
  • de photos d’objets sous diverses perspectives;
  • de dessins d’objets à trois dimensions reproduits de façons différentes.
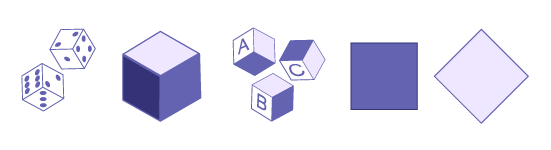
Des figures et solides carrées. La première figure est: « 2 dés. » La deuxième figure est: « un cube. » La troisième figure est: « 3 cubes. » La quatrième figure est: « un carré. » La cinquième figure est: « un carré plane donc le coin pointe en haut. »

Certaines et certains enfants peuvent se représenter certaines figures planes et certains solides, mais ne sont pas encore capables d’opérations réversibles. Dès que l’on modifie, par exemple, l’orientation d’un rectangle ou d’un cylindre, elles et ils ont tendance à penser que ce n’est plus la même figure ou le même solide. L’enfant ne comprend pas que certaines modifications topographiques ne changent pas les attributs mesurables de la figure plane ou du solide.

Exemple 1

Certaines et certains élèves croient que le premier carré est un bon carré alors que le second est un mauvais carré, puisque l’image mentale qu’elles et ils ont du carré correspond à celle qu’on leur a le plus fréquemment présentée.

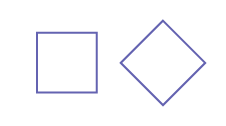
2 figures carrées. Le premier carré est: « sur la base. » La deuxième repose sur son sommet ».

Il faut donc les amener à réaliser qu’un carré reste un carré même s’il est placé différemment. La figure a toujours les mêmes propriétés : quatre côtés congrus et quatre coins droits.

Exemple 2

Certaines et certains élèves croient que le premier cylindre est un bon cylindre alors que le second est un mauvais cylindre, puisque l’image mentale qu’elles et ils ont du cylindre correspond à celle d’un cylindre déposé sur sa base.

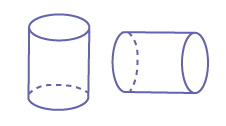
2 cylindres. Le premier cylindre est: « sur la base circulaire. » Le deuxième est : « placé sur son côté ».

Il faut donc les amener à réaliser qu’un cylindre reste un cylindre, même s’il est placé différemment. Le solide a toujours une face plane en forme de cercle et une surface courbe.

Exemple 3

Pour confirmer et compléter la représentation mentale que peut avoir l’élève d’une figure plane ou d’un solide, le personnel enseignant peut aussi utiliser les exemples et les non-exemples. Dans l’exemple qui suit, le terme waline est inventé. Ce genre de stratégie permet à l’élève de reconnaître un objet, une figure ou un solide en décrivant les propriétés qui les caractérisent et d’éliminer un objet, une figure ou un solide en décrivant les propriétés qui les différencient.

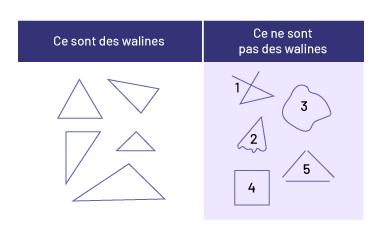
Tableau de 2 colonnes. La première colonne: « sont des walines. » La deuxième colonne: «Ce ne sont pas des walines. »

Figure 1 : Cette figure n’est pas une waline, car ce n’est pas un triangle. La figure 1 est formée d’une ligne brisée ouverte, tandis qu’un triangle est toujours formé d’une ligne brisée fermée.

Figure 2 : Cette figure n’est pas une waline, car ce n’est pas un triangle. La figure 2 est formée d’une ligne courbe et d’une ligne brisée, tandis qu’un triangle est toujours formé d’une ligne brisée fermée.

Figure 3 : Cette figure n’est pas une waline, car ce n’est pas un triangle. La figure 3 est formée d’une ligne courbe fermée, tandis qu’un triangle est toujours formé d’une ligne brisée fermée.

Figure 4 : Cette figure n’est pas une waline, car ce n’est pas un triangle. C’est un carré. Le carré est aussi formé d’une ligne brisée fermée, mais il a quatre côtés, quatre sommets et quatre coins.

Figure 5 : Cette figure n’est pas une waline, car ce n’est pas un triangle. Ce sont trois lignes droites. Un triangle est toujours formé d’une ligne brisée fermée.

Il est important de demander à l’élève non seulement d’encercler ou de reconnaître les walines, mais aussi d’expliquer son choix, et ce, afin de vérifier sa compréhension du concept de triangle et de modifier la façon de l’enseigner, si cela est nécessaire.

Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 36-38.

CONNAISSANCE : ATTRIBUT

Dès son arrivée à l’école, l’enfant reconnaît, nomme, compare et classe des objets en se servant d’attributs observables. Elle ou il peut identifier et décrire des objets en se servant d’un vocabulaire relatif aux caractéristiques de certains attributs tels la taille (par exemple, gros, petit, long, court, épais, mince), la couleur (par exemple, rouge, bleu), la texture (par exemple, doux, rugueux, soyeux, lisse), le déplacement (par exemple, roule, glisse), l’utilité (par exemple, pour construire une tour, pour produire une mosaïque) et le type de matériau des objets (par exemple, plastique, bois). Ces termes font partie de son vocabulaire usuel.

L’enfant repère visuellement des attributs semblables ou différents entre des objets et distingue facilement des formes d’objets familiers. Elle ou il est donc capable de reconnaître, de nommer, de comparer et de classer des objets en observant les ressemblances et les différences dans leur apparence.

Par l’observation et la manipulation, il s’agit d’amener l’enfant à reconnaître, à nommer, à comparer et à classer des objets ainsi que des figures géométriques en utilisant d’abord des mots qu’elle ou il connaît et en se servant d’un vocabulaire mathématique relatif aux propriétés géométriques (nombre de sommets, nombre de faces, nombre de côtés, nombre d’arêtes, sorte d’angles, sorte de lignes, axes de symétrie).

Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 32.

CONNAISSANCE : CRITÈRE DE CLASSEMENT

Voici des exemples de critères de classement qui peuvent être utilisés par les élèves.

  • Figures planes formées d’une ligne fermée brisée
  • Figures planes formées d’une ligne fermée courbe
  • Figures planes qui ont trois côtés
  • Figures planes qui ont quatre côtés
  • Figures planes sans côtés
  • Solides qui ont seulement des faces
  • Solides qui ont des faces et des surfaces
  • Solides qui ont seulement des surfaces

Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 35.