E1.2 Composer et décomposer des figures planes, et montrer que l’aire d’une figure reste constante, quelle que soit la façon dont ses parties sont organisées.
ACTIVITÉ 1 : TANGRAM (COMPOSER, DÉCOMPOSER DES FORMES GÉOMÉTRIQUES ET CONSERVATION DE L’AIRE)
Démarche
Remettre à chaque élève un carton carré.
Expliquer aux élèves qu’elles et ils vont créer leur propre tangram.
Présenter un tangram aux élèves, si cela est nécessaire.
Préciser que le carré doit être découpé en au moins six pièces.
Exemple
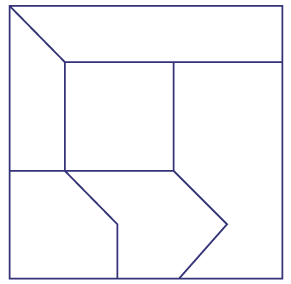
Demander aux élèves :
- de créer une autre forme avec les pièces de leur tangram et d’en tracer le contour;
- d’échanger leurs pièces et le contour tracé avec une ou un autre élève et d’essayer de recréer la forme.
Intervention
Inviter quelques élèves à venir expliquer, devant la classe, leur façon de procéder pour recréer la forme.
Poser des questions telles que :
- Que remarques-tu?
- Que peux-tu dire sur l’aire du carton carré?
- Si tu compares l’aire de ton tangram avec l’aire du tangram d’une ou d’un autre élève, que remarques-tu?
Faire ressortir que le carton carré peut être décomposé en figures planes plus petites et recomposé. L’aire demeure identique, même si cette figure plane a une apparence différente. L’aire demeure constante, peu importe les tangrams utilisés. Il s’agit du concept fondamental de conservation.
Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, p. 49-50.
ACTIVITÉ 2 : LES FIGURES EN ORDRE DE GRANDEUR (COMPARER)
Le personnel enseignant place, sur les quatre murs de la classe, six figures irrégulières différentes, parmi lesquelles deux paires de figures ont la même surface (voir Annexe 1). Il met à la disposition des élèves, des ciseaux, du papier cartonné, de la ficelle, des papillons adhésifs, des crayons, du papier quadrillé de 1 cm sur 1 cm (voir Annexe 2). Il présente la mise en situation suivante :
- Dans un concours de mathématiques, le défi suivant a été donné aux participants : « Sans utiliser de règle, place les figures suivantes en ordre, de celle ayant la plus petite surface à celle ayant la plus grande surface. »
- Vous avez le droit d’apporter une seule figure à la fois à votre pupitre et vous ne pouvez pas écrire dessus.
- Comment pouvez-vous résoudre ce problème?
Un échange mathématique doit suivre cette activité pour que les élèves puissent mettre en commun leur stratégie. Cette activité favorise la discussion et permet aux élèves de réaliser que plusieurs stratégies peuvent être adoptées pour résoudre le même problème.
Source : L'@telier - Ressources pédagogiques en ligne (atelier.on.ca), p. 1
