E1.2 Composer et décomposer des figures planes, et montrer que l’aire d’une figure reste constante, quelle que soit la façon dont ses parties sont organisées.
HABILETÉ : COMPOSER ET DÉCOMPOSER DES FIGURES PLANES
Composition et décomposition des figures planes
Lorsqu’elles et ils commencent l’école, la plupart des élèves sont en mesure de repérer des exemples de formes dans leur environnement. Les élèves savent aussi que les formes qu’elles et ils reconnaissent sont rarement isolées, et que plusieurs formes font partie de figures ou d’objets plus grands. Si on leur demandait par exemple de trouver des rectangles dans la classe, les élèves pourraient aussi remarquer que la fenêtre est constituée de panneaux de verre rectangulaire et que le couvercle fait partie d’une boîte où « les côtés et le fond sont des rectangles ».
L’enseignement doit aller au-delà de l’identification de figures planes et de solides. Il doit plutôt aider les élèves à comprendre les relations physiques entre les formes et les figures lorsqu’elles sont assemblées (composées) ou décomposées. Des activités de construction de structures à l’aide de formes géométriques (par exemple, mosaïques géométriques ou pièces de tangram), telles que créer de nouvelles formes par assemblage ou par décomposition, permettent aux élèves de réfléchir à la façon dont les formes géométriques s’assemblent à des fins fonctionnelles (par exemple, concevoir une machine) et esthétiques (par exemple, créer un modèle).
Créer des illustrations en assemblant des figures planes favorise la réflexion des élèves et les discussions sur la géométrie à deux dimensions. Les jeunes enfants traversent les étapes du développement (présentées ci-dessous) en assemblant des formes géométriques pour en faire des formes géométriques complexes (Clements, 2004). Même si des âges approximatifs sont indiqués pour chaque étape, la progression de l’élève dépend surtout de son expérience. Le personnel enseignant joue un rôle important à cet égard et doit proposer des activités créatives et démontrer la façon d’assembler des formes géométriques de plus en plus complexes.
Étapes du développement selon Clements
- Agencement (âge approximatif : 3 ans)
Les enfants utilisent des formes géométriques isolées pour représenter des objets ou des personnes, mais ne sont pas encore capables de les assembler pour créer une plus grande forme géométrique. Elles et ils pourraient par exemple utiliser trois formes géométriques pour représenter le soleil, une glissade et un bac à sable.
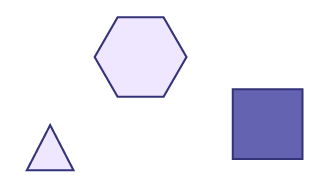
- Assemblage de formes individuelles (âge approximatif : 4 ans)
Les enfants assemblent des formes géométriques. Chaque forme géométrique représente une partie d’un objet ou d’une personne (par exemple, un losange pour représenter une jambe). Comme à l’étape précédente, l’enfant voit les formes géométriques comme un tout et ne perçoit que très peu de relations géométriques entre les formes géométriques ou les parties d’une forme géométrique.
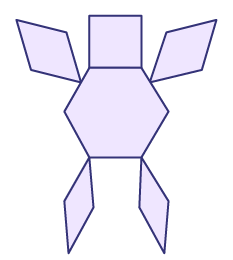
- Création par essais et erreurs (âge approximatif : 5 ans)
Les enfants assemblent des formes géométriques. Plusieurs formes géométriques représentent les parties d’un objet (par exemple, trois carrés pour le tronc d’un corps). Elles et ils procèdent par essais et erreurs pour créer de nouvelles formes géométriques.
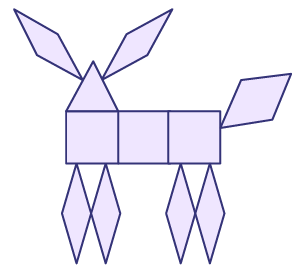
- Composition individuelle (âge approximatif : 5 ans)
Les enfants assemblent intentionnellement des formes géométriques et savent lesquelles s’agencent bien entre elles.
image Un animal qui ressemble à un ourson, et dont les parties du corps sont dessinées avec des
figures plane. La tête est un hexagone. Les oreilles sont des losanges. Le corps est un hexagone. Les bras et les
jambes sont formés de deux losanges, par membre.. Les pieds sont formés avec un losange.
- Substitution (âge approximatif : 6 ans)
Les enfants assemblent des ensembles de formes géométriques complexes et sont en mesure de substituer certaines formes géométriques pour d’autres (par exemple, six triangles verts pour créer un hexagone jaune à l’aide de mosaïques géométriques).
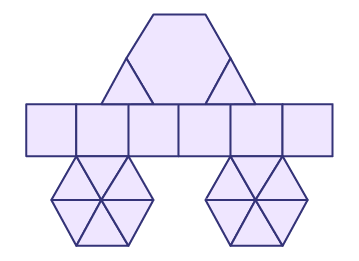image Un véhicule est formé de figures planes.La partie supérieure est faite d’un hexagone, deux
triangles sont placés l’un à la droite et le second à la gauche, pour servir de base à la partie supérieure. La partie
centrale est formée de 6 carrés égaux qui sont alignés. La partie inférieure représente les roues. Chaque roue est
formée de 6 triangles qui forment un hexagone.
- Reproduction de formes géométriques complexes (âge approximatif : 7 ans)
Les enfants construisent un motif à l’aide de formes géométriques et le répètent intentionnellement.
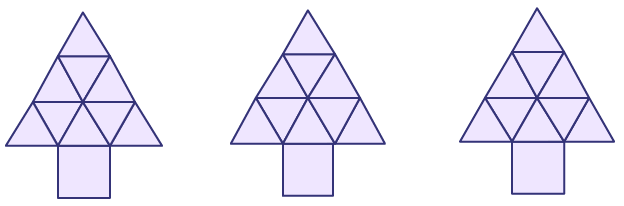
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 13-15.
HABILETÉ : MONTRER QUE L’AIRE D’UNE FIGURE RESTE CONSTANTE
Au cycle primaire, des concepts fondamentaux sont essentiels au développement de la compréhension des attributs mesurables. La conservation est un des concepts fondamentaux.
« Tant que les élèves n’ont pas appris à “conserverˮ, comme le dit Piaget, leurs comparaisons peuvent être déformées par un facteur conceptuel ou un autre. » [traduction libre]
(Copley, 2000, p. 132)
En mesure, la conservation désigne le concept selon lequel la mesure d’un attribut, en unités non conventionnelles ou conventionnelles, demeure la même que l’objet soit déplacé, transformé ou décomposé.
Il est important que le personnel enseignant demande régulièrement aux élèves de transformer, de déplacer ou de décomposer un objet et d’en comparer la mesure d’attributs quelconques, en unités non conventionnelles ou conventionnelles, avant et après la transformation.
Les élèves pourront ainsi se questionner, échanger leurs idées et découvrir les circonstances dans
lesquelles s’applique le concept de conservation.
Exemple du concept de conservation de l’aire
L’aire des figures 1 et 2 est la même que l’aire du carré, car les trois figures sont construites à partir des sept mêmes pièces d’un jeu de tangram.
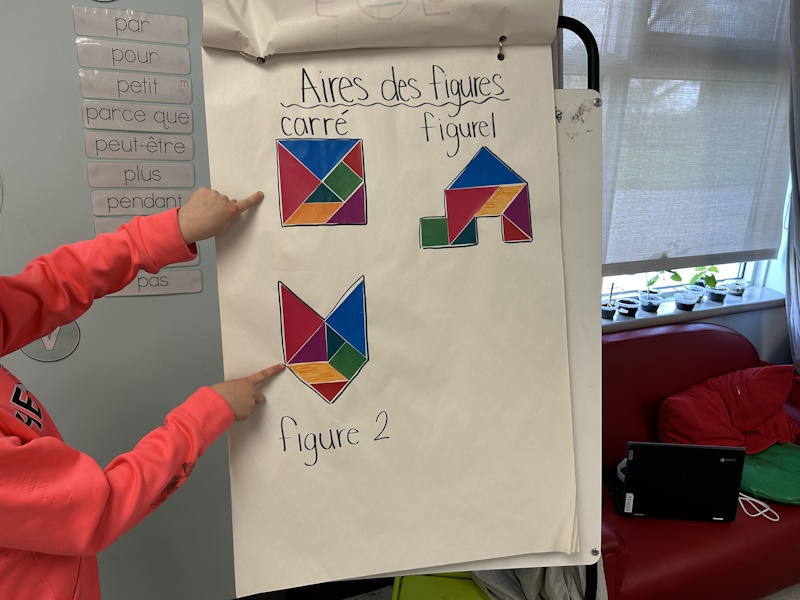
Source : Guide d'enseignement efficace des mathématiques de la maternelle à la 3e année, p. 53
L’élève qui comprend ce concept réalise que l’aire d’une surface demeure la même, que la surface soit déplacée, transformée ou décomposée.
Exemple
Luc choisit deux pentaminos et les assemble pour créer une figure. Il trace cette figure sur du papier quadrillé et colore les carrés qui font partie de cette figure. Il crée une autre figure avec les mêmes pentaminos. Que peut-on remarquer au sujet de l’aire des deux figures de Luc?
L’aire de chaque figure est identique; chacune occupe le même nombre de carrés, mais les pentaminos sont disposés différemment. L’aire n’a pas augmenté ou diminué; l’aire représente toujours l’aire de la surface des deux pentaminos choisis.
Additivité
Un autre concept fondamental à développer chez les élèves est celui de l’additivité. L’élève qui comprend ce concept réalise que l’aire d’une figure est égale à la somme de l’aire de chacune de ses parties.
Exemple
Sur un géoplan, une élève crée deux rectangles contigus. Elle estime et mesure l’aire de chaque rectangle. Avec un élastique de couleur différente, elle réunit les deux rectangles dans une même figure. Qu’observe-t-on en comparant l’aire de cette nouvelle figure avec celle des figures initiales?
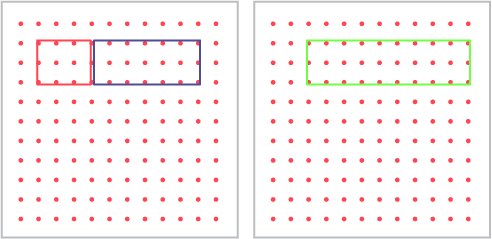
L’aire de la nouvelle figure est égale à la somme de l’aire des deux rectangles réunis. L’aire de l’exemple ci-dessus est : 6 unités carrées + 12 unités carrées = 18 unités carrées.
Source : Fiche de la maternelle à la 3e année Attribut, aire.
Une même aire peut prendre un nombre infini de formes.
On peut comparer deux aires directement en les superposant ou en les faisant correspondre pour déterminer celle des deux qui est la plus grande.
Pour mieux comparer deux aires en facilitant leur superposition et leur mise en correspondance, on peut décomposer l’une des deux aires et réorganiser ses parties pour former une nouvelle forme. Si l’aire reste la même, la comparaison est valide.
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020. Ministère de l'Éducation de l'Ontario.
CONNAISSANCE : AIRE
L’aire est le nombre servant à mesurer la surface d’une région plane ou l’espace qu’elle contient.
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020. Ministère de l'Éducation de l'Ontario.
Pour l’attribut aire, les élèves doivent visualiser un espace à deux dimensions, c’est-à-dire se faire une image mentale d’une surface plane ou courbe. Par exemple, dans une situation où il est question de déterminer l’aire d’un rectangle donné, les élèves doivent visualiser qu’il s’agit de déterminer la mesure de l’espace occupé par la surface de cette figure. Les élèves doivent aussi reconnaître que, dans certaines situations, l’attribut aire peut prendre un autre nom, par exemple :
- l’étendue d’un terrain;
- la superficie d’une ville.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3eannée, p. 21.
L’aire désigne la grandeur d’une surface ou d’un espace à deux dimensions.
Exemple
Je détermine l’aire de la face du haut de la boîte en la recouvrant de papillons adhésifs.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3eannée, p. 46.
Exemple
L’élève montre sa compréhension de l’aire en recouvrant la surface de mosaïques géométriques.
« J’ai utilisé quatre losanges bleus, quatre triangles verts et un hexagone jaune pour couvrir le cerf-volant. Les formes ne se chevauchent pas. »
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3eannée, p. 28.
Le personnel enseignant pose des questions telles que :
- Que remarques-tu?
- Quelle est l’aire du carré? Est-ce efficace comme stratégie pour mesurer l’aire? Quels changements pourrais-tu apporter?
- Peux-tu comparer l’aire de ton carré avec l’aire d’un carré d’une autre équipe? Que remarques-tu?
Le questionnement ouvert du personnel enseignant permet à l’élève d’approfondir sa compréhension du concept de l’aire. L’élève doit comprendre que, pour mesurer efficacement l’aire d’une figure plane, les unités de mesure doivent être placées sans espacement et sans chevauchement. Lorsque la figure plane est complètement recouverte de différentes unités de mesure non conventionnelles, une conversion est nécessaire pour arriver à une mesure de l’aire plus facile à communiquer. Par exemple, dans l’image précédente, l’élève peut remarquer que l’hexagone est formé de six triangles et que chacun des losanges contient deux triangles. L’aire pourrait donc être de 18 triangles.
L’élève modifie les mosaïques géométriques utilisées pour mesurer l’aire du carré en utilisant seulement des triangles verts et en s’assurant de ne laisser ni espace ni chevauchement entre les triangles.