E2.1 Utiliser des unités de mesure non conventionnelles de façon appropriée pour mesurer des longueurs, et décrire la relation inverse entre la taille de l’unité et le nombre d’unités nécessaire.
HABILETÉ : MESURER DES LONGUEURS AVEC DES UNITÉS DE MESURE NON CONVENTIONNELLES
La deuxième étape de l’acte de mesurer consiste, selon l’année d’études ou le degré de familiarité des élèves avec l’attribut à mesurer, à choisir une unité de mesure non conventionnelle ou conventionnelle appropriée pour mesurer un attribut quelconque d’un objet.
Pour ce faire, il importe de choisir une unité qui reflète l’attribut à mesurer et qui se prête bien à la situation. De plus, il est généralement préférable d’utiliser une même unité de mesure.
Étapes de l'acte de mesurer
- déterminer l'attribut à mesurer;
- choisir l'unité de mesure;
- déterminer la mesurer;
- communiquer le resultat.
Lors des premières explorations d’un attribut d’un objet, il est préférable que le personnel enseignant incite d’abord les élèves à choisir une unité de mesure non conventionnelle, et ce, afin de leur permettre de mieux comprendre le sens de l’attribut et de sa mesure.
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 83.
La troisième étape de l’acte de mesurer consiste à déterminer la mesure d’un attribut quelconque d’un objet, c’est-à-dire à donner un ordre de grandeur à l’attribut en le quantifiant en fonction d’une unité de mesure.
Selon la situation, l’élève utilise généralement l’une des stratégies ci-dessous pour déterminer une mesure :
- comparer et ordonner;
- juxtaposer des unités de mesure;
- utiliser un instrument de mesure.
Le choix de la stratégie dépend du contexte, de l’utilisation que l’on veut faire de la mesure, du degré de précision recherché et des instruments de mesure disponibles. Aux fins de ce contenu d’apprentissage, l’élève compare et ordonne puis juxtapose des unités de mesure non conventionnelles.
Comparer et ordonner
Comparer et ordonner implique la comparaison de deux objets en fonction d’un même attribut. Par exemple, pour donner une idée de la longueur de son crayon, une ou un élève peut comparer la longueur du crayon avec la longueur d’un stylo et conclure : « Mon crayon est un peu plus long que ce stylo. » Cette stratégie ne permet pas à proprement parler de quantifier la mesure d’un attribut d’un objet; elle permet simplement de fixer un ordre de grandeur de cet attribut en établissant qu’il est plus grand ou plus petit que le même attribut d’un autre objet connu. Soulignons que l’on utilise toutes et tous cette stratégie dans de nombreuses situations où l’on juge qu’il n’est pas vraiment nécessaire de quantifier la mesure.
Par exemple, afin de s’assurer qu’un papier d’emballage est suffisamment long pour permettre d’emballer une boîte, il suffit de comparer le périmètre de la boîte avec la longueur du papier en superposant successivement quatre des faces de la boîte sur le papier.
On compare la mesure d’un attribut de deux objets soit par comparaison directe, soit par comparaison indirecte.
Comparaison directe
Dès leur très jeune âge, les enfants comparent la mesure d’un attribut de deux objets par comparaison directe (par exemple, la longueur de deux tablettes de chocolat, leur taille par rapport à celle d’une ou d’un autre enfant). Elles et ils communiquent ensuite le résultat de façon descriptive plutôt que quantitative (par exemple, « cette tablette de chocolat est plus longue que celle-là », « je suis moins grand que toi »). La comparaison directe s’effectue habituellement soit en superposant un objet sur un autre, soit en plaçant les deux objets côte à côte ou dos à dos.
Exemple
Les élèves placent deux boîtes de céréales debout, l’une contre l’autre, et constatent qu’une boîte est plus haute que l’autre.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 89-91.
Comparaison indirecte
Lorsqu’il est difficile ou impossible de comparer directement deux objets en fonction d’un même attribut, on peut effectuer une comparaison indirecte, c’est-à-dire comparer la mesure de l’attribut pour chacun des objets avec une troisième mesure. Par exemple, on pourrait se servir d’enjambées pour mesurer la longueur d’un corridor de l’école et ensuite comparer cette mesure avec le nombre d’enjambées nécessaire pour parcourir la longueur d’un autre corridor.
L’habileté à comparer divers attributs d’objets par la comparaison indirecte contribue au développement du concept de transitivité. Il importe donc que le personnel enseignant incite les élèves à effectuer une comparaison directe ou indirecte avec autant d’attributs que possible.
Juxtaposer des unités de mesure
Juxtaposer des unités de mesure consiste à placer soigneusement un certain nombre d’objets étalons comme unités de mesure de façon à égaler une distance pour déterminer sa longueur.
Exemple
Une élève détermine la longueur d’un carton en utilisant de petits et de grands trombones comme objets étalons. Elle dispose bout à bout une série de trombones de chaque grandeur pour couvrir la distance entre les deux extrémités du carton. Elle dénombre ensuite les trombones utilisés et conclut, par exemple, que la longueur du carton est égale à la longueur de 14 petits trombones ou à la longueur de 8 grands trombones.
Juxtaposer des unités de mesure permet de quantifier la mesure d’un attribut quelconque d’un objet, habituellement en fonction d’unités de mesure non conventionnelles. Cette stratégie est particulièrement utile pour aider les élèves à développer leur compréhension de l’attribut longueur, puisque la mesure de l’attribut est exprimée en fonction d’objets étalons concrets plutôt que de mesures conventionnelles plus abstraites telles que des centimètres. Elle permet aussi aux élèves de mieux comprendre les concepts d’itération et de structure associée aux unités de mesure.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 91-93.
Concept fondamental : Structure associée aux unités de mesure
L’élève qui comprend ce concept réalise que les unités de mesure de longueur sont juxtaposées dans un espace à une dimension, sans espace ni chevauchement, de façon à recouvrir la distance entre deux extrémités d’un objet.
Exemple
« Quatre élèves de 1re année ont mesuré la largeur de napperons identiques à l’aide de bâtonnets, mais ont des résultats différents. Qui a mesuré avec exactitude? Explique pourquoi. »
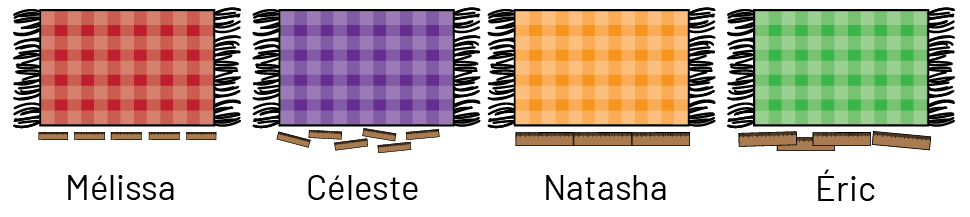image Le
napperon rouge de Mélissa est mesuré avec 5 petits bâtons qui sont légèrement espacés.Le napperon violet de Céleste
est mesuré avec 6 petits bâtons qui sont légèrement désalignés.Le napperon jaune de Natasha est mesuré avec 3 bâtons
plus grands, ils sont parfaitement disposés.Le napperon vert d’Éric est mesuré avec 4 grands bâtons désalignés
Natasha a mesuré avec exactitude, car elle a utilisé des bâtonnets identiques et les a placés en ligne droite le long d’un côté du napperon sans laisser d’espace et sans chevauchement.
Source : Fiche de la maternelle à la 3e année Attribut longueur, p. 4.
HABILETÉ : DÉCRIRE LA RELATION INVERSE ENTRE LA TAILLE DE L’UNITÉ ET LE NOMBRE D’UNITÉS NÉCESSAIRE POUR MESURER DES LONGUEURS
L’analyse de relations, qui est toute aussi importante dans le domaine Mesure (Sens de l’espace) que dans celui de l’Algèbre, mène les élèves à formuler une généralisation. Pour ce faire, elles et ils peuvent suivre un processus informel comme celui-ci :
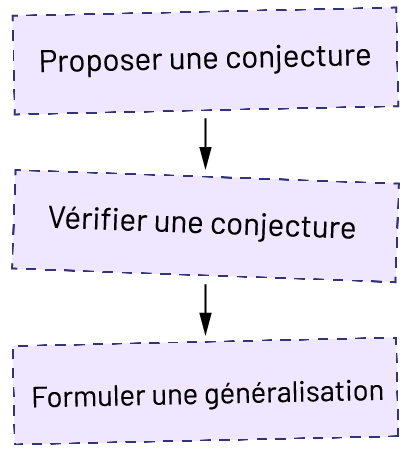
L’analyse des relations permet aux élèves de développer leur sens de la mesure, ainsi que leur compréhension des unités de mesure conventionnelles.
Relation inverse
Le nombre d’unités requis pour déterminer la mesure d’un attribut est inversement proportionnel à la grandeur de l’unité de mesure utilisée. Autrement dit :
- plus l’unité de mesure utilisée est petite, plus le nombre d’unités requis pour déterminer la mesure de l’attribut est grand;
- plus l’unité de mesure utilisée est grande, plus le nombre d’unités requis pour déterminer la mesure de l’attribut est petit.
Par exemple, si une élève utilise une cuillère à soupe et un autre élève utilise une cuillère à café pour déterminer la capacité d’un contenant, ils découvrent qu’ils utilisent un plus grand nombre de cuillères à café que de cuillères à soupe pour déterminer la capacité de ce contenant étant donné que l’unité de mesure de la cuillère à café est plus petite que l’unité de mesure de la cuillère à soupe.
Exemple
Le carton a une longueur de 14 petits trombones. Si je mesure le carton avec de grands trombones, j’aurai besoin de moins de trombones.
Quoique le concept de relation inverse puisse sembler évident dans ce genre de situation, il pose problème pour plusieurs élèves qui sont plus habituées et habitués à des situations de relation directe (par exemple, plus grande est la distance à parcourir en autobus, plus grande sera la durée du trajet). Afin de les aider à bien comprendre ce concept, le personnel enseignant doit leur présenter diverses situations concrètes de mesure qui les incitent à établir ce lien.
Lorsque les élèves saisissent bien le concept de relation inverse entre le nombre d’unités requis pour déterminer une mesure et la grandeur de cette unité, elles et ils peuvent plus facilement comprendre et établir des relations entre certaines des unités de mesure conventionnelles. Par exemple, établir et déterminer la relation entre le mètre (m) et le centimètre (cm).
Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, p. 60-61.
CONNAISSANCE : UNITÉS DE MESURE NON CONVENTIONNELLES
Une unité de mesure non conventionnelle ne fait pas partie d’un système uniforme et reconnu, comme le système métrique. L’interprétation d’une unité de mesure non conventionnelle peut donc différer d’une personne à une autre, étant donné la nature subjective du choix d’unité (par exemple, dire qu’une longueur mesure trois gommes à effacer peut être interprété différemment selon la gomme à effacer utilisée par une autre personne).
Les élèves peuvent utiliser une variété d’unités de mesure non conventionnelles pour mesurer des longueurs. En voici des exemples.
- Objets de la vie quotidienne : longueur d’un trombone, d’un cure-dents, d’un stylo, d’une paille
- Repères personnels : largeur d’un doigt, taille, longueur du pied, taille de la main ou longueur d’un bras, enjambées
- En classe : longueur d’une réglette
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
CONNAISSANCE : ATTRIBUT LONGUEUR
La longueur est le terme général utilisé pour désigner toute grandeur d’un espace à une dimension que l’on mesure à l’aide d’un objet étalon.
Une longueur peut désigner :
- la grandeur d’un segment, c’est-à-dire la distance entre deux points;
- la distance entre deux droites parallèles ou deux plans parallèles;
- un périmètre;
- une hauteur, une profondeur, une épaisseur, une largeur, une taille (d’une personne).
Note : Pour certaines et certains élèves, ces différents termes associés à la longueur peuvent prêter à confusion. Le terme « grandeur » utilisé dans la description des attributs longueur, aire et capacité désigne ce qui peut être estimé, évalué ou mesuré.
Exemples
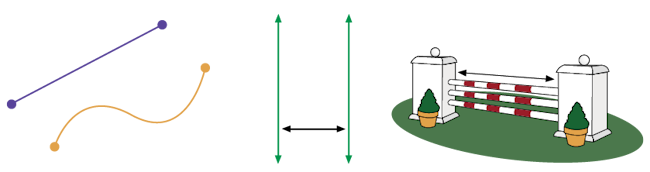image Deux points reliés par une droite.Deux points reliés par une ligne
courbe.Deux doubles flèches, vertes. Elles sont parallèles. Entre elles est placée une double flèche noire, elle se
place perpendiculairement par rapport aux autres doubles flèches.Un obstacle pour les chevaux. Une flèche est placée
entre les deux socles verticaux.
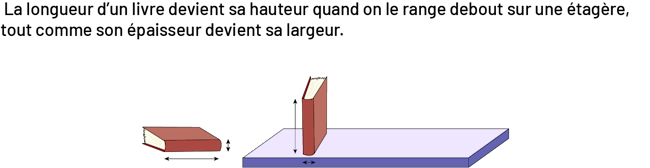image
Deux
livres. Le premier livre est déposé sur le plat de sa couverture. Une flèche montre la longueur du livre et une autre
flèche montre son épaisseur.Le second livre est debout sur une étagère, une flèche montre sa hauteur et une seconde
flèche montre son épaisseur.
Source : Fiche de la maternelle à la 3e année Attribut longueur,p. 2.
CONNAISSANCE : CONCEPT FONDAMENTAL D’ITÉRATION
En mesure, l’itération désigne l’acte de placer, à plusieurs reprises et d’une manière ordonnée, un même objet étalon ou une même unité de mesure de façon à déterminer la mesure d’un attribut quelconque. Le nombre de fois que l’unité de mesure est placée correspond alors à la mesure de l’attribut.
Exemple 1
On peut utiliser une main comme unité de mesure non conventionnelle pour mesurer la longueur d’une table. Il suffit de placer successivement la main, sans espace ni superposition, de façon à couvrir la distance d’une extrémité à l’autre de la table. On peut alors déterminer, par exemple, que la longueur de la table est équivalente à trois longueurs de main. Cette itération permet de visualiser la relation entre la longueur totale de la table et la longueur de la main, et donne un sens à la mesure obtenue.
L’itération implique une action concrète. Elle se prête particulièrement bien aux situations qui font appel aux attributs longueur et aire.
Voici une vidéo qui montre un exemple avec l’itération d’un pouce.
Source : Ministère de l’Éducation. (2007). La largeur du pouce.
Exemple 2
« Comment peux-tu utiliser la longueur d’une paille comme unité de mesure pour estimer et mesurer la hauteur d’une amie ou d’un ami? »
(Placer successivement la paille, sans espace ou superposition, de façon à couvrir la distance entre les pieds et la tête de la personne, et déterminer le nombre de fois que la paille a été placée.)
Source : Fiche de la maternelle à la 3e année Attribut longueur, p. 2.
Il importe donc que l’itération soit explorée tôt dans le cadre de l’enseignement de la mesure afin de bien construire ce concept fondamental. En effet, c’est ce concept qui permet aux élèves de comprendre qu’une grandeur peut être perçue non seulement comme un tout, mais aussi comme une somme de parties plus petites. C’est seulement après avoir compris cette relation entre la partie (l’unité de mesure) et le tout (l’attribut mesuré) que les élèves peuvent vraiment saisir le sens d’une mesure quelconque.
Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, p. 48-49.