E1.1 Classer, construire et identifier des cubes, des prismes, des pyramides, des cylindres et des cônes en comparant les faces, les sommets, les arêtes et les angles.
ACTIVITÉ 1 : ACTIVITÉS TECHNOLOGIQUES (CONSTRUIRE DES FORMES GÉOMÉTRIQUES)
Démarche
Construire à l’ordinateur, à l’aide du logiciel AppleWorks ou d’un autre logiciel, différentes formes géométriques.
Note : Ce genre d’activité permet de reconnaître et de comparer des solides en fonction du nombre d’arêtes, de sommets et de faces, du type de faces et de la congruence des faces ou des figures planes, du nombre de sommets, de côtés, de la longueur des côtés...
Intervention
Poser des questions telles que :
- Quel solide n’a que des faces triangulaires? Sont-elles congruentes?
- Quels solides ont une base carrée?
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 49.
ACTIVITÉ 2 : JE REMPLIS LE TABLEAU (RECONNAÎTRE, NOMMER, COMPARER ET CLASSER DES SOLIDES)
Démarche
Présenter aux élèves le tableau ci-dessous.
Demander aux élèves de mettre un crochet dans la deuxième colonne lorsque la propriété s’applique aussi au prisme à base carrée.
|
Propriétés du cube |
Propriétés du prisme à base carrée |
|
6 faces |
|
|
8 sommets |
|
|
12 arêtes |
|
|
6 faces congrues |
Intervention
Poser des questions telles que :
- Quelle différence y a-t-il entre un cube et un prisme à base carrée?
- Comment les deux solides sont-ils semblables?
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 50-51.
ACTIVITÉ 3 : SOLIDE MYSTÈRE (RECONNAÎTRE LES SOLIDES)
Matériel
solides
Déroulement
Placer sur une table à la vue des élèves les solides suivants : un cube, un prisme à base carrée, un prisme à base rectangulaire, une pyramide à base triangulaire, une pyramide à base carrée, une sphère, un cône et un cylindre.
Inviter une ou un élève à choisir, sans le pointer ni le nommer, un solide mystère et à vous informer discrètement de son choix.
Demander aux autres élèves de découvrir le solide mystère en posant des questions qui se répondent par oui ou par non. Préciser que les questions posées doivent porter sur les propriétés des solides. L’élève qui a choisi le solide répond aux questions.
L’élève qui trouve le solide mystère en choisit un à son tour et fait deviner son choix par les autres.
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 78.
ACTIVITÉ 4 : JEU DE DEVINETTES
Voici mon train composé de trois wagons :
- mon premier wagon a six faces congrues;
- mon dernier wagon a seulement un sommet remarquable (un apex).
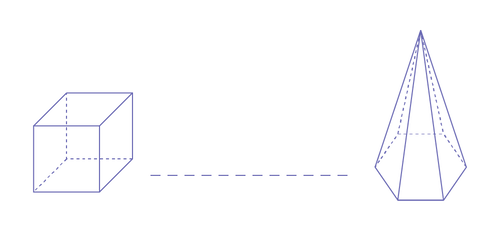
Trouver le wagon du milieu par son nom et en fonction de la propriété qui le relie aux deux autres. Plusieurs réponses sont possibles.
Exemple : Mon wagon du milieu est le prisme à base rectangulaire.
- Le prisme à base rectangulaire ressemble au cube, car il a aussi huit sommets.
- Le prisme à base rectangulaire ressemble à la pyramide à base hexagonale, car il a aussi 12 arêtes.
Demander aux élèves d’inventer leurs propres devinettes et de les poser en classe.
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 127-128.
ACTIVITÉ 5 : DES SOLIDES BIZARRES
Demander aux élèves de faire des cubes, des prismes et des sphères avec de la pâte à modeler.
Enlever un morceau des solides.
Demander aux élèves de nommer et de décrire les nouveaux solides.
Si le nouveau solide ne ressemble à aucun solide connu, créer un nom bizarre.
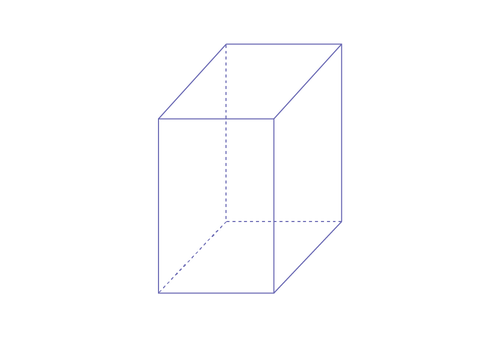
Exemple 1
Trancher le coin d’un cube, comme dans l’illustration ci-dessous.

On choisit d’appeler le nouveau solide un cubi, un presquecube, un cubo...
Il a sept faces, douze arêtes et sept sommets. Trois faces sont carrées et congruentes. Les quatre autres faces sont en forme de triangle. Une des faces est plus grande que les trois autres.
Exemple 2
Trancher le coin d’un prisme à base rectangulaire, comme dans l’illustration ci-dessous.
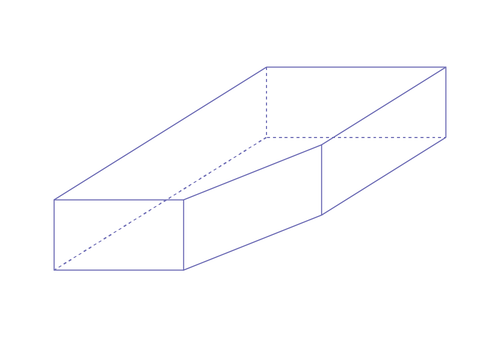
On choisit d’appeler le nouveau solide un prismo, un pentaprisme...
Il a sept faces, quinze arêtes et dix sommets. Il a cinq faces rectangulaires. Les deux autres faces sont en forme de pentagone et elles sont congruentes.
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 128-129.
