À vue d'oeil...

E2.9 Utiliser des centimètres carrés (cm²) et des mètres carrés (m²) pour estimer, mesurer et comparer l’aire de diverses figures planes, y compris celles avec des lignes courbes.

HABILETÉ : ESTIMER L’AIRE DE DIVERSES FIGURES PLANES, Y COMPRIS CELLES AVEC DES LIGNES COURBES

---

Habileté à estimer

Les adultes, tout comme les élèves, doivent déterminer des grandeurs de façon approximative dans une variété de situations quotidiennes. Autrement dit, elles et ils doivent estimer (par exemple, estimer le nombre de mosaïques qu’il faut pour couvrir une surface).

En mesure, estimer est un processus fondé sur des renseignements visuels et sur des expériences antérieures qui permet de porter un jugement par rapport à la grandeur approximative d’un attribut quelconque (par exemple, longueur, aire, capacité, temps) sans recourir à une stratégie de mesure.

Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3^e année, p. 16.

Le centimètre carré et le mètre carré servent à quantifier l’aire. Bien qu’ils soient tous deux des carrés à la base, ils peuvent être décomposés pour prendre n’importe quelle forme (par exemple, un carré peut devenir deux triangles, ou des figures planes ayant des lignes courbes et des lignes droites, ou encore quatre plus petits carrés).

Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1^re à la 8^e année, 2020, Ministère de l'Éducation de l'Ontario.

Habileté : mesurer et comparer l’aire de diverses figures planes, y compris celles des lignes courbes en utilisant Des centimètres carrés et des mètres carrés

---

En 3^e année, les élèves mesurent l’attribut de l’aire avec des unités non conventionnelles (par exemple, des mosaïques géométriques) et avec des unités conventionnelles, telles que des centimètres carrés et des mètres carrés.

Exemples 

• Utiliser des centimètres carrés pour estimer et mesurer l’aire d’une variété de figures planes, y compris des polygones.

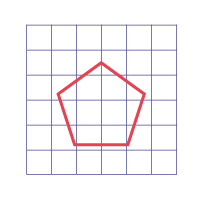
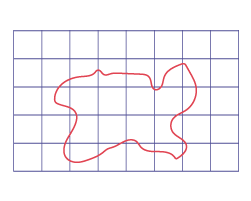
• Utiliser des centimètres carrés pour estimer et mesurer l’aire de diverses figures planes ayant des lignes courbes.

• Le carré permet de recouvrir un papier quadrillé ou une grille sans créer de chevauchement ni laisser d’espaces, et c’est la forme habituellement utilisée comme unité d’aire. Un carré dont un côté mesure une unité (c’est-à-dire un carré-unité) a une aire d’une unité carrée. Toute unité de mesure conventionnelle (c’est-à-dire une unité du système métrique ou du système impérial) peut devenir une unité d’aire conventionnelle.
• Le centimètre carré et le mètre carré servent à quantifier l’aire. Bien qu’ils soient tous deux des carrés à la base, ils peuvent être décomposés pour prendre n’importe quelle forme (par exemple, un carré peut devenir deux triangles, ou des figures planes ayant des lignes courbes et des lignes droites, ou encore quatre plus petits carrés).
• On mesure l’aire en comptant les unités entières ou partielles nécessaires pour recouvrir une surface. Par exemple, une surface entièrement recouverte par dix-huit carrés de 1 unité chacune a une aire de 18 unités carrées. 
• Les formes et les objets choisis pour représenter des centimètres carrés et des mètres carrés doivent garder une aire constante, même s’ils sont disposés de manière à prendre d’autres formes. On peut compter les unités partielles et les combiner pour former des unités entières afin d’obtenir la mesure la plus exacte possible.

Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1^re à la 8^e année, 2020, Ministère de l'Éducation de l'Ontario.

Mesure de la longueur, le diamètre, la circonférence, le périmètre et l’aire

Concepts fondamentaux

Au cycle primaire, des concepts fondamentaux sont essentiels au développement de la compréhension des attributs mesurables. Entre autres, le concept de la structure associée aux unités de mesure.

Structure associée aux unités de mesure de l’aire d’un rectangle

L’élève qui comprend ce concept réalise que les unités de mesure d’aire d’un rectangle doivent être juxtaposées dans un espace à deux dimensions, sans espace ni chevauchement, de façon à recouvrir le rectangle selon une disposition rectangulaire constituée de colonnes et de rangées.

Exemple 

« Comment Zoé peut-elle déterminer l’aire de son livre de bibliothèque en utilisant une feuille de papier quadrillé? »

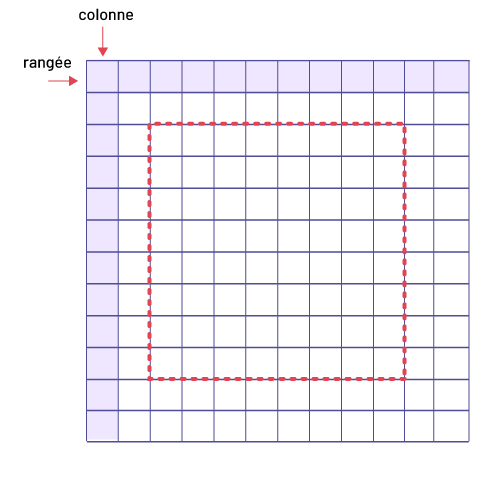
Zoé trace d’abord le contour de son livre sur une feuille de papier quadrillé. Elle compte ensuite le nombre de colonnes (huit) et de rangées (neuf) à l’intérieur du contour du livre. Elle détermine donc que l’aire de son livre de bibliothèque est égale à 72 unités carrées.

Relations

En explorant l’aire des figures planes, les élèves commencent à établir des relations entre les dimensions d’un objet et ses attributs.

Exemple 1 : Relation entre les dimensions d’un rectangle et son aire

En 3^e année, alors que les élèves recouvrent un rectangle de carreaux ou d’une feuille de papier quadrillé transparente pour déterminer la grandeur de la surface d’un napperon, le personnel enseignant pose les questions suivantes :

– Si les côtés horizontaux du napperon étaient plus longs, est-ce que j’utiliserais plus de carreaux, moins de carreaux ou la même quantité de carreaux pour déterminer l’aire de sa surface?

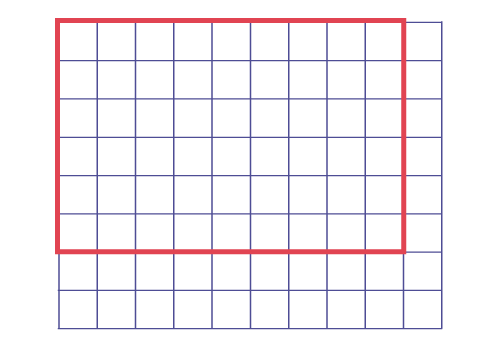
– Si les côtés verticaux du napperon étaient plus courts, est-ce que j’utiliserais plus de carreaux, moins de carreaux ou la même quantité de carreaux pour déterminer l’aire de sa surface?

Les élèves découvrent qu’à mesure que la longueur de la base d’un rectangle augmente, son aire augmente (relation entre la base et l’aire).

Les élèves découvrent qu’à mesure que la longueur de la hauteur d’un rectangle augmente, son aire augmente (relation entre la hauteur et l’aire).

Cette relation peut être très bien démontrée à l’aide d’un tableau interactif.

Exemple 2 : Relation entre les dimensions d’un rectangle et le nombre de colonnes et de rangées

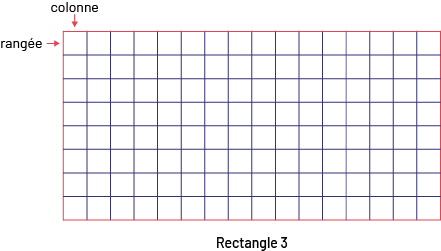
Pour amener les élèves à établir des liens entre les dimensions d’un rectangle et son aire, le personnel enseignant aide les élèves à observer la relation entre le nombre d’unités de longueur d’un côté et le nombre d’unités carrées dans la rangée ou la colonne lorsqu’on mesure la surface. Elle ou il présente, au tableau, plusieurs rectangles aux élèves et leur demande de déterminer la longueur de la base et, ensuite, le nombre d’unités carrées dans la rangée.

En faisant ces observations, les élèves pourront plus facilement établir les relations entre les mesures de la base ou de la hauteur et le nombre de rangées ou de colonnes d’un rectangle. Par la suite, au cycle moyen, elles et ils pourront mieux comprendre la raison pour laquelle on peut déterminer l’aire d’un rectangle en appliquant la formule A = b × h.

Absence de relation

Il importe également que le personnel enseignant propose aux élèves des activités qui leur permettent d’explorer des situations dans lesquelles il n’y a pas de relation. Ce type d’activité permet aux élèves de mieux comprendre l’importance de vérifier une conjecture avant de conclure qu’elle est vraie ou de formuler une généralisation.

Les exemples ci-dessous illustrent le fait que quelques élèves croient à tort que deux rectangles de même périmètre ont la même aire et inversement (Exemples 1 et 2).

Exemple 1 

Le personnel enseignant demande aux élèves si des figures planes ayant des aires égales ont aussi les mêmes périmètres. Une ou un élève dit : « Je pense que, si des figures planes ont des aires égales, elles ont aussi les mêmes périmètres. » Le personnel enseignant demande aux autres élèves si elles et ils pensent que cette conjecture est vraie ou fausse. Il forme des équipes de deux et leur suggère de vérifier la conjecture. Pour ce faire, il leur propose la démarche suivante. Le personnel enseignant remet aux élèves un ensemble de tangram, des feuilles de papier quadrillé, de la ficelle et une paire de ciseaux. Il leur demande ensuite d’utiliser toutes les pièces du tangram pour construire trois formes de leur choix.

Dans chaque cas, l’élève doit :

• tracer le contour de la forme sur la feuille de papier quadrillé;
• déterminer le nombre d’unités carrées qui couvrent la surface;
• tracer le contour de la forme avec de la ficelle et la couper à la bonne longueur;
• coller la ficelle au tableau à côté de la ficelle précédente;
• inscrire les mesures des périmètres et des aires dans le tableau ci-dessous.

Lors de l’échange mathématique, le personnel enseignant demande aux élèves d’observer les résultats et de constater que :

• toutes les figures ont la même aire puisqu’elles sont assemblées avec les mêmes pièces;
• toutes les figures n’ont pas le même périmètre.

Les élèves peuvent alors conclure que la conjecture est fausse, c’est-à-dire que si des figures planes ont la même aire, elles n’ont pas nécessairement le même périmètre.

Exemple 2 

Le personnel enseignant demande aux élèves si des figures planes qui ont le même périmètre ont la même aire. Une ou un élève dit : « Je pense que, même si des figures planes ont le même périmètre, elles n’ont pas nécessairement la même aire. » Le personnel enseignant demande aux autres élèves si elles et ils pensent que cette conjecture est vraie ou fausse. Il forme des équipes de deux et leur suggère de vérifier la conjecture. Pour ce faire, il leur propose la démarche suivante.

Le personnel enseignant demande aux élèves de dessiner sur une feuille de papier quadrillé le plus grand nombre de rectangles différents ayant un périmètre de 16 unités.

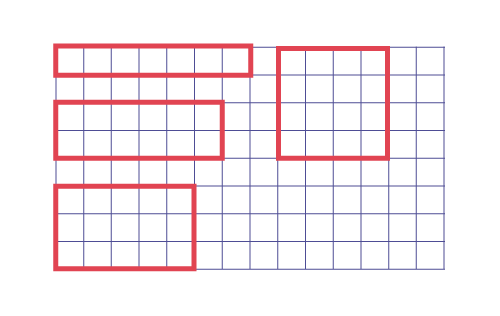
Pour chaque rectangle, l’élève doit :

• tracer le contour du rectangle sur la feuille de papier quadrillé;
• déterminer le périmètre et l’aire de la figure;
• inscrire les mesures du périmètre et de l’aire dans son journal mathématique.

Lors de l’échange mathématique, le personnel enseignant demande aux élèves d’observer les résultats et de constater que :

• toutes les figures ont un périmètre de 16 cm;
• toutes les figures n’ont pas la même aire.

Les élèves peuvent alors conclure que la conjecture est vraie, c’est-à-dire que si des figures planes ont le même périmètre, elles n’ont pas nécessairement la même aire.

Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3^e année, p. 68-73.

CONNAISSANCE : UNITÉS DE MESURE CONVENTIONNELLES (CENTIMÈTRE CARRÉ ET MÈTRE CARRÉ)

---

Le centimètre carré et le mètre carré sont des unités d’aire conventionnelles du système métrique.

• Un carré dont les dimensions sont de 1 cm sur 1 cm a une aire d’un centimètre carré (1 cm²).
• Un carré dont les dimensions sont de 1 m sur 1 m a une aire d’un mètre carré (1 m²).
• Le centimètre carré et le mètre carré servent à quantifier l’aire. Bien qu’ils soient tous deux des carrés à la base, ils peuvent être décomposés pour prendre n’importe quelle forme (par exemple, un carré peut devenir deux triangles, ou des figures planes ayant des lignes courbes et des lignes droites, ou encore quatre plus petits carrés).

Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1^re à la 8^e année, 2020, Ministère de l'Éducation de l'Ontario.