E1.2 Situer et lire des coordonnées dans le premier quadrant d’un plan cartésien, et décrire les déplacements d’une coordonnée à l’autre à l’aide de translations.
HABILETÉ : SITUER DES COORDONNÉES DANS LE PREMIER QUADRANT D’UN PLAN CARTÉSIEN
Pour situer un point ou un couple de coordonnées dans le premier quadrant d’un plan cartésien, par exemple A (2, 4), il faut se déplacer de deux unités vers la droite à partir de l’origine, puis de quatre unités vers le haut.
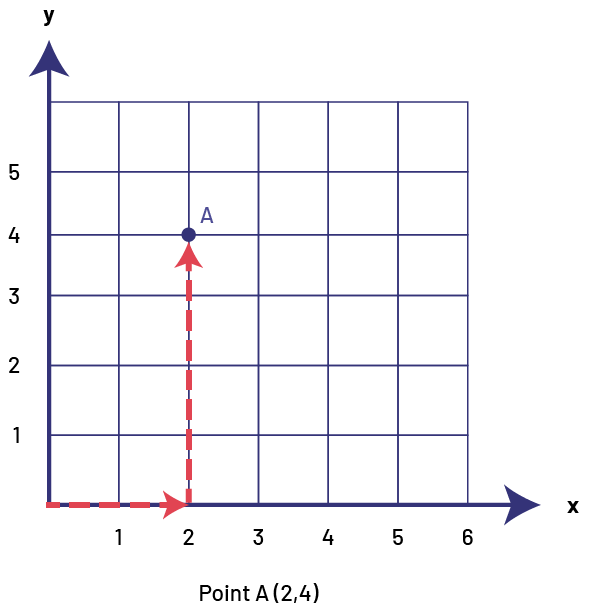
Il faut souligner aux élèves l’importance de l’ordre dans lequel sont placés les nombres dans les coordonnées cartésiennes. Pour ce faire, il suffit de leur demander de situer, par exemple, les points A (2, 4) et B (4, 2); les élèves se rendront rapidement compte que ces points décrivent des positions différentes.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 25.
HABILETÉ : LIRE DES COORDONNÉES DANS LE PREMIER QUADRANT D’UN PLAN CARTÉSIEN
Pour lire des coordonnées dans le premier quadrant d’un plan cartésien, il faut repérer les nombres sur les droites verticales et horizontales. Il faut lire le nombre qui correspond à la position horizontale du point par rapport à l’origine en premier et le nombre qui correspond à la position verticale du point par rapport à l’origine par la suite. Les élèves doivent comprendre que les coordonnées cartésiennes, par exemple (2, 4), définissent un des points d’intersection des droites et non une des cases formées par celles-ci.
Source : adapté de Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 25.
HABILETÉ : DÉCRIRE DES DÉPLACEMENTS D’UNE COORDONNÉE À L’AUTRE À L’AIDE DE TRANSLATIONS
Sur un plan cartésien, les déplacements se rapportent à la distance et à la direction. Si un point se déplace et change de coordonnées, il subit une translation.
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
Pour décrire une translation horizontale ou verticale, les élèves utilisent des mots, des lettres ou des symboles (par exemple, une translation de trois unités vers la droite est représentée symboliquement par 3 D ou 3 →). Pour décrire une translation oblique, il faut indiquer à la fois le déplacement horizontal et le déplacement vertical. Pour ce faire, les élèves utilisent une notation symbolique entre parenthèses. Par exemple, une translation de trois unités vers la droite et de deux unités vers le bas est représentée symboliquement par (3 D, 2 B) ou (3 →, 2 ↓). L’ordre des symboles n’a pas d’importance. Cependant, il est préférable d’habituer les élèves à toujours décrire la translation en indiquant d’abord le déplacement horizontal et ensuite le déplacement vertical.
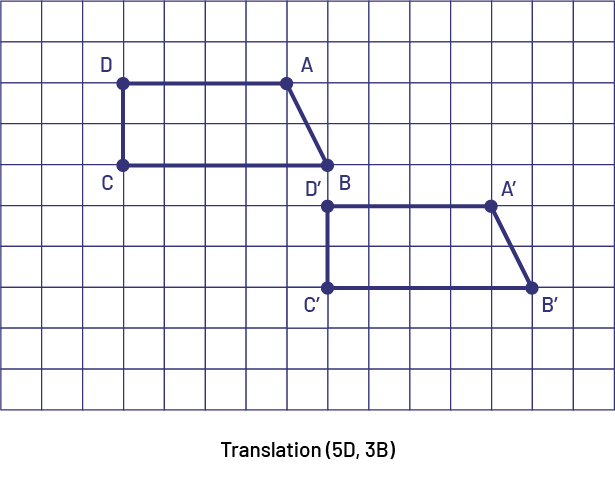image Grille comportant 15 colonnes et dix rangées. Il y a deux quadrilatères obliques sur la grille.
Les points « a », « b », « c », et « d » sont identifiés sur le premier quadrilatère. Les points « a » apostrophe, « b
» apostrophe, « c » apostrophe, et « d » apostrophe sont identifiés sur le deuxième quadrilatère.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 28.
CONNAISSANCE : PLAN CARTÉSIEN
Le plan cartésien est un système de repérage cartésien pour situer avec précision la position d’un point dans un plan.
Plan cartésien
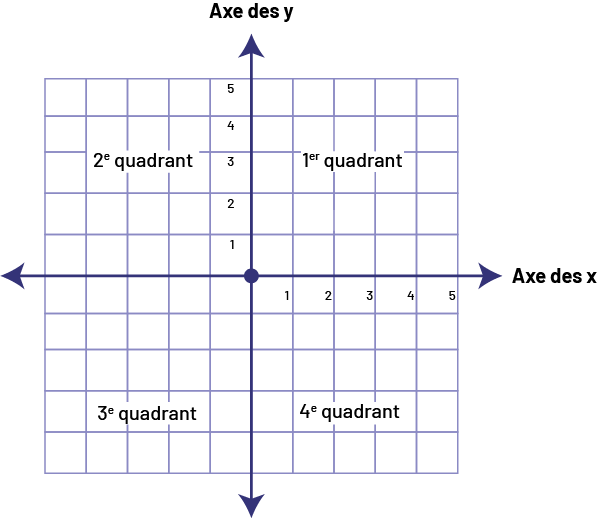image Un plan cartésien constitué de quatre quadrants, partant du coin
supérieur droit et allant du sens inverse des aiguilles d’une montre. Dans le premier quadrant, cinq rangées sont
numérotées soit sur l’axe horizontal des « x » et cinq colonnes sur l’axe vertical des « y ». Le point d’origine à
l’intersection de deux axes est marqué par un point.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 24.
CONNAISSANCE : UNE COORDONNÉE
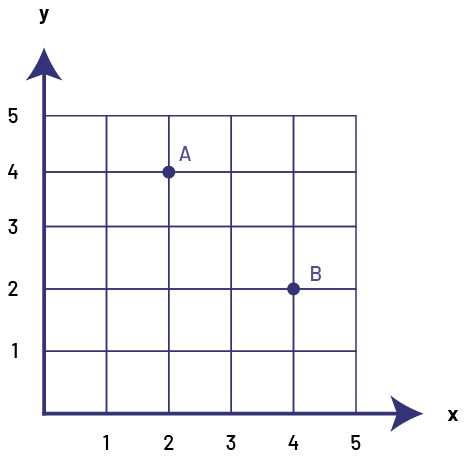
Le système de coordonnées cartésiennes permet de situer un point dans ce plan. Les coordonnées sont écrites entre parenthèses et sont séparées par une virgule comme suit : le point A (2, 4). Par convention, le premier nombre, appelé abscisse, indique la position horizontale du point par rapport à l’origine, et le second, appelé ordonnée, indique sa position verticale. À noter que les élèves de 4e année n’ont pas à utiliser le vocabulaire abscisse et ordonnée.
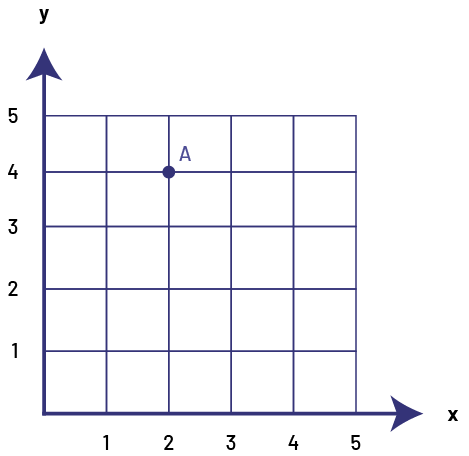image Une
grille comportant cinq rangées et cinq colonnes. Les rangées sont numérotées sur l’axe horizontal, soit « x » et sur
l’axe vertical, soit « y ». Il y a un point « a » situé à l’intersection « x » deux et « y » quatre, et un point « b »
situé à l’intersection « x » quatre et « y » deux.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 25.
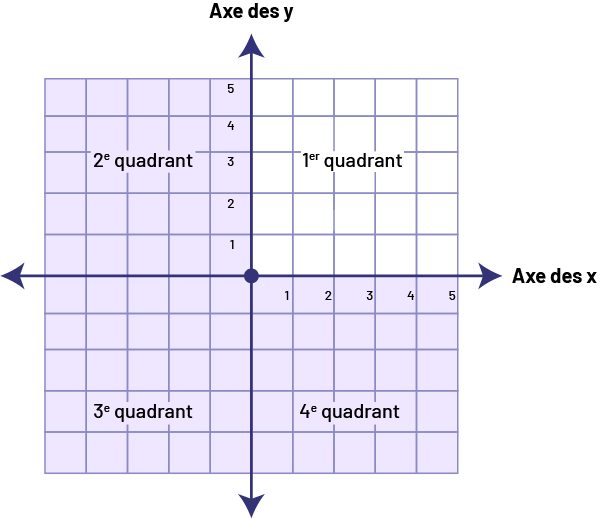
CONNAISSANCE : LE PREMIER QUADRANT D’UN PLAN CARTÉSIEN
Les axes x et y divisent le plan cartésien en quatre régions appelées quadrants. Les élèves de 4e année utilisent seulement le quadrant au haut et à la droite dans le plan cartésien, soit le premier quadrant.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 24.
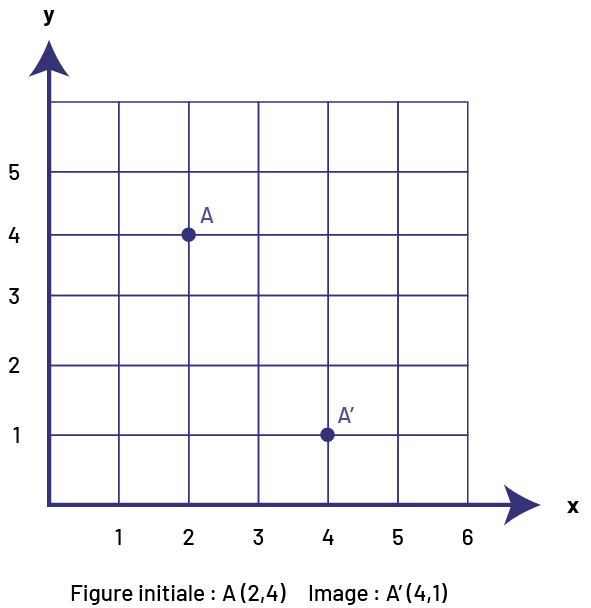
CONNAISSANCE : LE DÉPLACEMENT D’UNE COORDONNÉE
Le déplacement d’une coordonnée consiste à changer l’emplacement d’un point dans un plan cartésien à une position horizontale ou à une position verticale différente.
Exemple
Le point (2, 4) subit un déplacement de deux unités vers la droite (2D) et de trois unités vers le bas (3B). Ses nouvelles coordonnées sont (4, 1).
CONNAISSANCE : UNE TRANSLATION
La translation est définie par sa grandeur et sa direction (représentées symboliquement par des coordonnées ou par une flèche). Elle représente un déplacement linéaire, horizontal, vertical ou oblique dans lequel la figure initiale et l’image sont congruentes. La distance entre chaque point sur la figure initiale et le point correspondant sur l’image est constante. L’orientation de l’image est la même que l’orientation de la figure initiale.
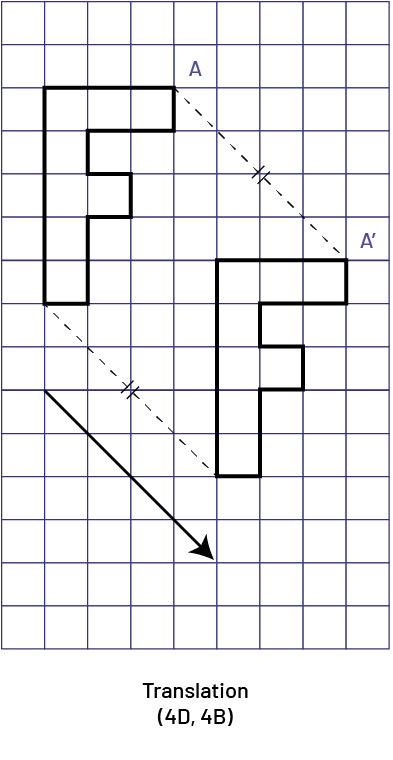image Une
grille de neuf colonnes et 15 rangées. Il y a deux lettres « f » placées obliquement sur la grille. Les points « a »
des deux « f » sont connectés par un trait. Une autre ligne parallèle connecte les bas du « f ». Il y a une flèche
diagonale qui pointe à la droite, vers le bas.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 36-37.
CONNAISSANCE : AXE HORIZONTAL
Deux axes perpendiculaires servent à définir le plan cartésien. L’axe horizontal est désigné par un x et est appelé l’axe des x.
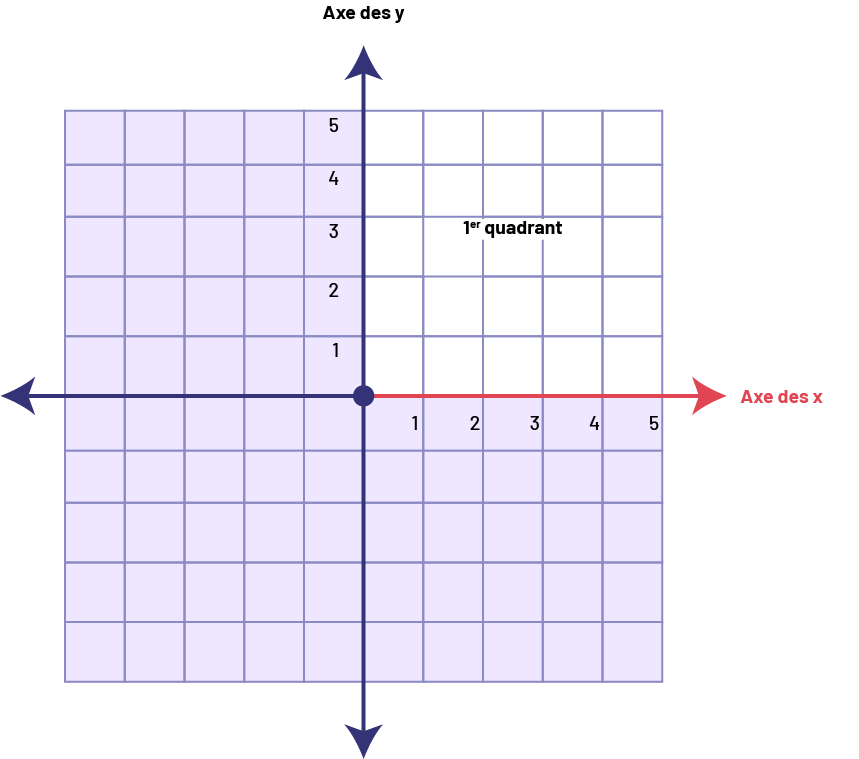
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 24.
CONNAISSANCE : AXE VERTICAL
Deux axes perpendiculaires servent à définir le plan cartésien. L’axe vertical est désigné par un y et est appelé l’axe des y.
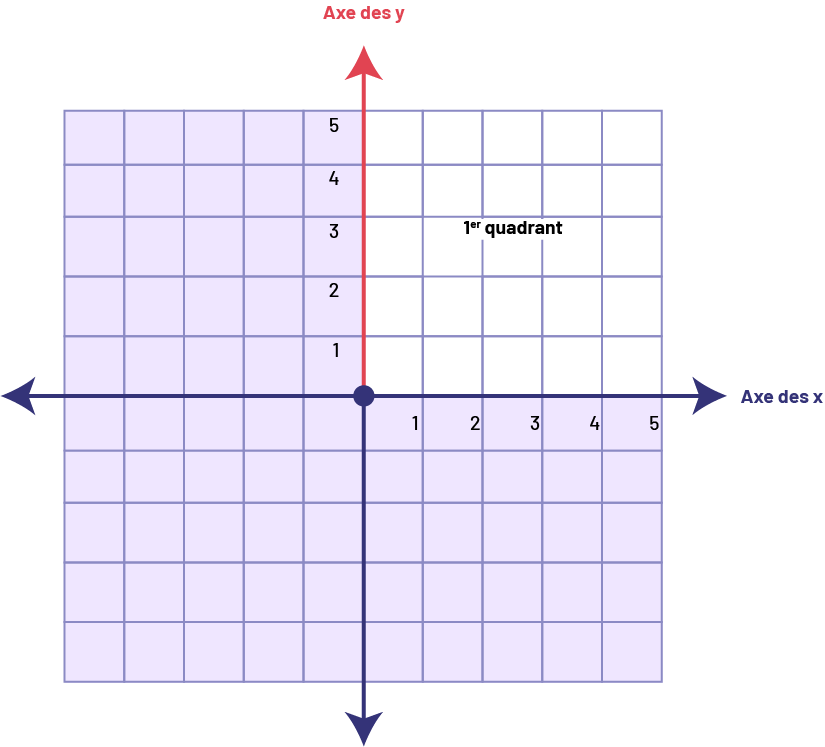
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 24.
CONNAISSANCE : POINT D’ORIGINE
Le point de rencontre de l’axe horizontal et de l’axe vertical, qui sert de point de repère, est le point d’origine.
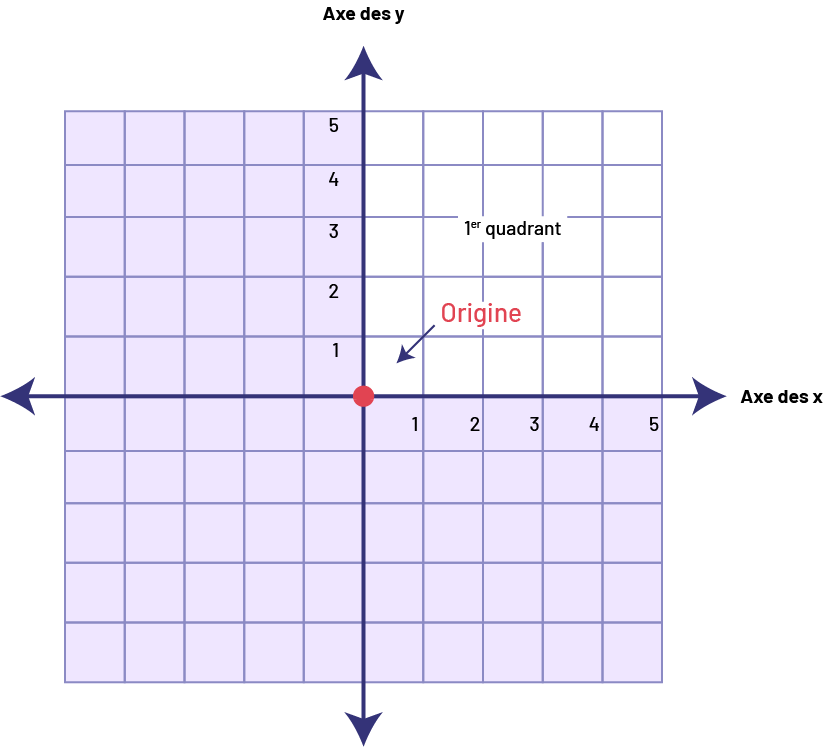image Un plan cartésien constitué de quatre quadrants. Seul le premier quadrant est identifié. Dans ce
dernier, cinq rangées sont numérotées sur l’axe horizontal des « x » et cinq colonnes sur l’axe vertical des « y ». Le
point d’origine à l’intersection de l’axe « x » et « y » est identifié par un point rouge.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 24.