E2.1 Utiliser des unités de mesure métriques appropriées pour estimer et mesurer la longueur, l'aire, la masse et la capacité.
HABILETÉ : ESTIMER DES MESURES
À compter de la fin du cycle primaire, les élèves doivent apprendre à utiliser diverses stratégies pour effectuer des estimations dans des situations de plus en plus complexes en utilisant, à la fois, des unités de mesure non conventionnelles et conventionnelles. Il importe donc que le personnel enseignant planifie des interventions et un enseignement formel axé sur des stratégies d'estimation particulières. Van de Walle et Lovin (2008a, p. 296-297) proposent l’enseignement de quatre stratégies d’estimation. Ces stratégies sont présentées dans le tableau suivant.
|
Stratégie |
Exemple |
|
Développer et utiliser des repères qui représentent des unités de mesure importantes Les élèves qui se sont constitué un répertoire de repères et qui les utilisent régulièrement à estimer avec plus d'efficacité et d'aisance. L'estimation de la mesure de l'attribut se fait en le comparant à un repère. |
Pour estimer la mesure d'un angle donné, l'angle droit et l'angle plat peuvent servir de repères. En superposant mentalement l'image de ces angles sur l'angle donné, les élèves peuvent conclure que la mesure est beaucoup plus près de 90o que de 180o. La mesure de l'angle donné est d'environ 100o. 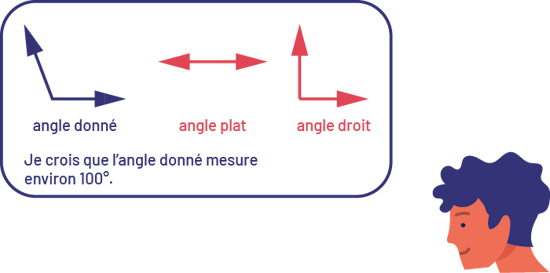 image Dans un rectangle arrondi se trouvent trois angles:
soit un angle donné qui est formé d’une courte ligne verticale et d’une courte ligne diagonale vers la
gauche, un angle plat, et un angle droit. Au bas du rectangle est écrit: je crois que l’angle donné mesure
environ cent degrés. À l’extérieur du rectangle, il y a un personnage. image Dans un rectangle arrondi se trouvent trois angles:
soit un angle donné qui est formé d’une courte ligne verticale et d’une courte ligne diagonale vers la
gauche, un angle plat, et un angle droit. Au bas du rectangle est écrit: je crois que l’angle donné mesure
environ cent degrés. À l’extérieur du rectangle, il y a un personnage.
|
|
Décomposer l'objet en parties Dans certains contextes, il est plus facile d'estimer la grandeur d'un objet en estimant d'abord la grandeur de plus petites sections facilement identifiables. L'estimation de la mesure de l'attribut correspond à la somme de la grandeur de chacune des sections. |
Pour estimer la hauteur d'un édifice de 12 étages, les élèves peuvent d'abord estimer que la hauteur du premier étage est d'environ 3 m. En supposant que tous les étages ont la même hauteur, ils peuvent alors estimer que l'édifice mesure environ 36 m de haut. 
|
|
Utiliser des subdivisions Si l’objet à mesurer ne comporte pas d’éléments qui suggèrent une façon de le décomposer en parties, on peut d’abord le diviser mentalement ou concrètement en demis. On peut ensuite diviser une de ces moitiés à nouveau en demis et répéter ainsi le processus jusqu’à l’obtention d’une section dont on peut estimer la mesure. |
Pour estimer l’aire d’une grande couverture, les élèves peuvent la plier en deux à répétition jusqu’à ce qu’ils obtiennent une surface de couverture relativement petite. Il leur suffit alors d’estimer l’aire de cette surface, puis de multiplier le résultat par le nombre de ces surfaces ainsi créées. 
Note : Les élèves peuvent établir des liens avec le domaine Modélisation et algèbre et explorer la relation entre le nombre de plis et le nombre de surfaces créées en pliant, par exemple, une feuille de papier et en notant dans un tableau le nombre de surfaces identiques obtenues après chaque pli. Ils pourraient alors souligner que chaque fois qu’on ajoute un pli, le nombre de surfaces est doublé. 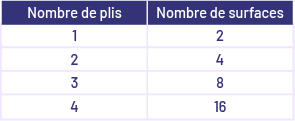
|
|
Faire des itérations mentalement et concrètement L’itération désigne l’acte de placer, à plusieurs reprises et d’une manière ordonnée, une même unité de mesure de façon à déterminer la mesure d’un attribut quelconque. L’estimation de la mesure de l’attribut correspond au nombre de fois que l’unité est placée. |
Pour estimer l’aire d’un carton en utilisant un papillon autocollant comme unité de mesure, les élèves peuvent tenter de visualiser le nombre de fois qu’un papillon peut être placé sur le carton sans faire de chevauchements ni laisser d’espaces. 
|
Lorsque les élèves effectuent des activités d'estimation de façon régulière, elles et ils se rendent compte qu'il n'y a pas qu'une seule stratégie efficace d'estimation. Le personnel enseignant doit donc leur proposer de fréquentes activités d'estimation ayant trait aux attributs mesurables. Ces activités s'avèrent pertinentes si les élèves échangent, discutent, justifient et expliquent la façon dont elles et ils sont parvenus à leurs résultats. Les explications et les justifications des estimations qu'ont faites les élèves permettent au personnel enseignant de connaître et même d'évaluer la compréhension qu'elles et ils ont des concepts et des procédures en mesure.
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 18-19.
HABILETÉ : UTILISER DES UNITÉS DE MESURE MÉTRIQUES APPROPRIÉES
L'acte de mesurer comporte une série de réflexions, de décisions et d'actions qui mènent à l'obtention et à la communication d'une mesure exacte et appropriée à un contexte donné. Pour ce faire, il faut franchir différentes étapes qui sont les mêmes pour tous les attributs à l'étude au cycle moyen, soit les attributs longueur, aire, angle, capacité, masse et temps. Quoique le nombre et l'identification de ces étapes varient quelque peu, selon les chercheuses et les chercheurs, elles peuvent en général être articulées de façon séquentielle comme suit :
- déterminer l'attribut à mesurer;
- choisir l'unité de mesure;
- déterminer la mesure;
- communiquer le résultat.
Déterminer l'attribut à mesurer
Dans toute situation-problème qui fait appel à l'acte de mesurer, la première étape est de déterminer l'attribut de l'objet qui doit être mesuré. Est-ce, par exemple, la longueur, l'aire, la capacité, la masse? Pour être en mesure de déterminer l'attribut à mesurer dans une situation donnée, les élèves doivent bien comprendre le sens de chacun de ces attributs. Le personnel enseignant doit donc leur proposer diverses situations d'apprentissage qui les incitent à s'interroger sur ce que les divers attributs d'un objet représentent et à choisir celui qui leur permettra de résoudre le problème.
Choisir l'unité de mesure
La deuxième étape de l'acte de mesurer consiste à choisir une unité de mesure non conventionnelle ou conventionnelle appropriée pour mesurer un attribut quelconque de l'objet. Pour ce faire, il importe de choisir une unité de mesure qui reflète l'attribut à mesurer et qui se prête bien à la situation. De plus, il est généralement préférable d'utiliser une seule et même unité de mesure. Enfin, il importe aussi que le choix de l'unité de mesure tienne compte du degré de précision de la mesure recherché (par exemple, une mesure de masse au kilogramme près ou au gramme près).
Source : Guide d'enseignement
efficace des mathématiques de la 4e à la 6e année, p. 83-86.
Cependant, la précision n'est pas toujours la meilleure option. Si elle n'est pas nécessaire, elle constitue une
perte de temps et complique la prise de mesure.
Lorsqu'il s'agit de choisir l'unité de mesure appropriée, les mêmes préfixes métriques s'appliquent à tous les attributs (sauf le temps) et désignent les relations entre les unités. La première des unités plus grandes qu'une unité donnée est 10 fois plus grande, et la première des unités plus petites qu'une unité donnée est 10 fois plus petite.
| Préfixe métrique | kilo- | déca- | Aucun préfixe | centi- | milli- | ||
|---|---|---|---|---|---|---|---|
| Valeur unitaire | 100 unités | 10 unités | 1 unité | \(\frac{1}{10}\) d'unité | \(\frac{1}{1000}\) d'unité | ||
| Valeur de position | unité de mille | centaine | unité | dixième | centième |
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
HABILETÉ : MESURER LA LONGUEUR, L'AIRE, LA MASSE ET LA CAPACITÉ
Déterminer la mesure
Le nombre de fois que l'unité de mesure est contenue dans la grandeur est la mesure. C'est donc un nombre abstrait qui exprime le rapport entre la grandeur de l'objet et l'unité choisie (X. Roegiers, Les mathématiques à l'école primaire, tome 2, 2000, p. 115, cité dans cité dans Ministère de l'Éducation de l'Ontario, Guide d'enseignement efficace des mathématiques, de la 4e à la 6e année – Mesure, 2010, p. 89).
La troisième étape de l'acte de mesurer consiste à déterminer la mesure d'un attribut quelconque de l'objet, c'est-à-dire à donner un ordre de grandeur à l'attribut en le quantifiant en fonction d'une unité de mesure.
Étapes de l'acte de mesurer
- déterminer l’attribut à mesurer;
- choisir l’unité de mesure;
- déterminer la mesure;
- communiquer le résultat.
Utiliser un instrument de mesure
Un grand nombre d'instruments de mesure (par exemple, règle, thermomètre, balance) ont été conçus pour déterminer la
mesure de divers attributs en fonction d'unités de mesure conventionnelles. Même si cette stratégie permet d'obtenir
une mesure rapidement, elle requiert toutefois, de la part de la personne qui l'utilise, un bon sens de la mesure et
une bonne capacité d'abstraction. Afin d'aider les élèves à comprendre l'importance de ces instruments de mesure et la
façon de les utiliser correctement, le personnel enseignant peut leur proposer d'en fabriquer un.
Les élèves comprendront probablement mieux le fonctionnement des instruments de mesure si [elles et] ils
fabriquent des instruments de mesure simples basés sur des modèles d'unités qui leur sont familiers. […] Il est
essentiel que les élèves comparent le dispositif non conventionnel avec l'instrument classique. Si les élèves
n'ont pas l'occasion de faire cette comparaison, [elles et] ils risquent de ne pas comprendre que ces deux
instruments permettent d'arriver au même résultat (J. Van de Walle et L. H. Lovin, L'enseignement
des mathématiques : L'élève au centre de son apprentissage, tome 2, 2008, p. 272, cités dans
Ministère de l'Éducation de l'Ontario, Guide d'enseignement efficace des mathématiques, de la 4e à la
6e année – Mesure, 2010, p. 93).
Au cycle moyen, il importe que les élèves apprennent à utiliser certains des instruments de mesure usuels tels que ceux énumérés dans le tableau ci-dessous en tenant compte du degré de précision recherché et de l'importance de l'exactitude de la mesure.
|
Attribut |
Instruments |
|
Longueur |
|
|
Masse |
|
|
Capacité |
|
Dans toute situation faisant appel à une mesure, le degré de précision recherché détermine la taille de l'unité de mesure qui doit être utilisée. Il est défini en fonction du besoin ou de l'intention de la mesure. Dans certaines situations, par exemple, il peut suffire de savoir que la hauteur d'un cadre de porte mesure environ 2 m. Cette mesure, donnée au mètre près, demeure toutefois approximative, et son degré de précision est peu élevé. Il est fort probable que la hauteur du cadre mesure en réalité un peu moins ou un peu plus de 2 m. Si l'on veut fabriquer une porte pour la poser dans le cadre, il est nécessaire d'obtenir une mesure ayant un degré de précision plus élevé. Il faut alors utiliser des unités de mesure plus petites, c'est-à-dire des unités correspondant à des fractions de mètre (par exemple, des centimètres). On pourrait alors déterminer que la hauteur du cadre de porte mesure, au centimètre près, 213 cm.
Les élèves doivent reconnaître l'importance de choisir une unité de mesure qui correspond au degré de précision qu'impose, de façon explicite ou implicite, la situation de mesure. Afin de déterminer, par exemple, le temps qu'elles et ils prennent pour courir 100 mètres, les élèves peuvent choisir d'utiliser un chronomètre afin d'obtenir une mesure à la seconde près. Cependant, elles et ils reconnaissent qu'aux Jeux olympiques, il est nécessaire de mesurer au centième de seconde près le temps que prennent les athlètes pour courir 100 mètres.
L'exactitude de la mesure dépend de la manière dont on se sert de l'instrument de mesure, c'est-à-dire du respect des
modalités d'utilisation de l'instrument. Si l'instrument n'est pas utilisé correctement, la mesure obtenue ne sera pas
exacte; elle sera supérieure ou inférieure à la grandeur mesurée. Pour aider les élèves à bien comprendre la bonne
façon d'utiliser un instrument de mesure donné, le personnel enseignant peut d'abord modeler son utilisation.
Quelques précisions relatives aux modalités d'utilisation de certains instruments de mesure sont
présentées ci-dessous.
Pour utiliser correctement une règle, il faut :
- aligner une des extrémités de l'objet sur le zéro ou au début des lignes de graduation;
- s'assurer que la ligne de vision de l'autre extrémité de l'objet forme un angle de 90° avec la règle (voir Erreur de parallaxe dans l'illustration ci-dessous);
- dénombrer, sur la règle, les unités qui vont d'une extrémité à l'autre de l'objet.
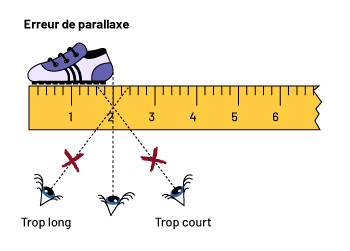 image Une règle de six centimètres. Par-dessus, il y a un soulier, au-dessus duquel est écrit: erreur
de parallaxe. Sous la règle, il y a trois yeux, lesquelles sont liés à la règle par trois lignes pointillées
différentes. Au-dessus du premier œil, il y a un « x » et en dessous est écrit: trop long. Au-dessus du troisième œil,
il y a un « x » et en dessous est écrit: trop court.
image Une règle de six centimètres. Par-dessus, il y a un soulier, au-dessus duquel est écrit: erreur
de parallaxe. Sous la règle, il y a trois yeux, lesquelles sont liés à la règle par trois lignes pointillées
différentes. Au-dessus du premier œil, il y a un « x » et en dessous est écrit: trop long. Au-dessus du troisième œil,
il y a un « x » et en dessous est écrit: trop court.
Pour utiliser correctement une balance à deux plateaux, il faut :
- placer la balance sur une surface horizontale plane;
- s'assurer que la balance et les plateaux sont en équilibre avant de placer l'objet à mesurer sur un des plateaux;
- déposer l'objet à mesurer sur un des plateaux et, mettre dans l'autre plateau, une des unités de masse choisies (par exemple, une masse de 1 g);
- ajouter des unités de masse jusqu'à ce que les deux plateaux soient de nouveau en équilibre;
- dénombrer les unités de masse utilisées.

Pour utiliser correctement la balance à triple fléau, il faut :
- placer la balance sur une surface horizontale plane;
- s'assurer que la flèche pointe vers le zéro avant de placer l'objet à mesurer sur le plateau;
- placer l'objet à mesurer au centre du plateau;
- déplacer les masses coulissantes, une à la fois, en commençant toujours par la plus grande masse (par exemple, la masse de 100 g, puis celle de 10 g et finalement, celle de 1 g) et en s'assurant de toujours placer les masses dans une des encoches;
- s'assurer que la flèche pointe toujours au-dessus du zéro avant de déplacer une masse vers la prochaine encoche;
- si la flèche pointe sous le zéro, reculer la masse d'une encoche et déplacer la prochaine masse (plus petite);
- procéder ainsi jusqu'à ce que la flèche pointe vers le zéro;
- lire la masse de l'objet en fonction des graduations où sont insérées chacune des trois masses.

Pour utiliser correctement une éprouvette graduée, il faut :
- s'assurer de placer l'éprouvette sur une surface horizontale plane;
- y verser lentement le liquide en prenant soin de ne pas créer de bulles d'air;
- s'assurer de se placer de façon à lire le volume de liquide en tenant compte du ménisque;
- lire le volume de liquide en fonction de la graduation indiquée sur la paroi de l'éprouvette (par exemple,
100 ml).
On appelle ménisque la courbure de la surface d'un liquide dans un récipient. Dans une éprouvette, un liquide tel que l'eau colle à la paroi, et le ménisque prend une forme concave. La lecture du volume de liquide doit se faire au point le plus bas du ménisque. De plus, la lecture doit s'effectuer à la hauteur des yeux.

Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 89-98.
Communiquer le résultat
La quatrième et dernière étape de l'acte de mesurer consiste à communiquer le résultat. Une fois que les élèves ont déterminé la mesure d'un attribut quelconque de l'objet, le personnel enseignant doit les inciter à montrer leur compréhension de la mesure obtenue en communiquant clairement leur résultat à l'aide du vocabulaire mathématique et des unités de mesure appropriées.
Étapes de l'acte de mesurer
- déterminer l’attribut à mesurer;
- choisir l’unité de mesure;
- déterminer la mesure;
- communiquer le résultat.
Après avoir déterminé, par exemple, que la hauteur de la colonne de liquide (mercure ou alcool) du thermomètre de la salle de classe correspond au nombre 20, certaines et certains élèves peuvent être portés à dire simplement : « Il fait 20. » Le personnel enseignant doit les amener à toujours exprimer leur résultat en mentionnant l'attribut et l'objet mesuré, ainsi que l'unité de mesure utilisée (par exemple, « La température dans la salle de classe est actuellement égale à 20 °C. »). Elle ou il peut aussi les inciter à montrer leur compréhension de ce résultat en le comparant à une autre mesure ou à une autre situation (par exemple, « C'est une température confortable; il fait moins chaud que dehors. ») Le tableau ci-après présente divers exemples d'une communication claire liée aux différents attributs de mesure à l'étude.
|
Attribut mesuré |
Unité de mesure choisie |
Quantité |
Communication du résultat |
|
Longueur d’un cahier |
centimètre |
25 |
La longueur du cahier est de 25 cm. |
|
Masse d’un seau rempli d’eau |
kilogramme |
8 |
Le seau rempli d’eau a une masse de 8 kilogrammes. |
|
Aire de la surface d’une boîte |
centimètre carré |
168 |
L’aire de la surface de la boîte est égale à 168 cm2. |
|
Capacité d’une tasse à café |
millilitre |
300 |
La tasse à café a une capacité de 300 ml. |
Le personnel enseignant doit s'assurer que les élèves savent lire correctement les symboles lorsqu'ils communique leur résultat oralement. Les élèves doivent dire, par exemple :
- « La longueur du cahier est de 25 centimètres. » et non « La longueur du cahier est de 25 c-m. »;
- « L'aire de la surface de la boîte est égale à 168 centimètres carrés. » et non « L'aire de la surface de la boîte est égale à 168 c-m à l'exposant 2. »
Le personnel enseignant doit aussi s'assurer que les élèves savent écrire correctement les symboles représentant les diverses unités de mesure en respectant les conventions établies. Pour cela, au moment de l'échange mathématique, il doit poser aux élèves des questions en utilisant une formulation qui fait clairement référence à l'attribut afin de les aider à développer l'habileté à communiquer clairement un résultat de mesure. Elle ou il devrait leur demander, par exemple : Quelle est la capacité du verre? et non Combien d'eau le verre contient-il?; Quelle pomme a la plus grande masse? et non Quelle pomme est la plus lourde?
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 102-105.
Connaissance : repères associés à l'attribut longueur
Puisque les repères sont essentiellement des images mentales, leur conception est intimement liée à l'habileté à visualiser. Les élèves n'ont généralement pas trop de difficulté à concevoir des repères appropriés pour l'attribut longueur; par exemple, l'image mentale de la longueur d'un côté d'un petit cube emboîtable pour représenter 1 cm, celle de la largeur d'une porte pour représenter 1 m ou celle de la longueur de 2,5 tours de piste pour représenter 1 km.
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 14.
Connaissance : repères associés à l'attribut aire
Puisque les repères sont essentiellement des images mentales, leur conception est intimement liée à l'habileté à visualiser. Les élèves n'ont généralement pas trop de difficulté à concevoir des repères appropriés pour l'attribut aire; par exemple, l'image mentale de l'aire d'une face d'un petit cube emboîtable pour représenter 1 cm2.
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 14.
Connaissance : repères associés à l'attribut masse
Selon Lindsay et Scott (Estimating Eggs : An Activity to Help to Promote the Exploration of Mass Estimation
Concepts, 2005, p. 3), il est très difficile de concevoir des repères pour l'attribut masse en
raison de la différence entre l'acuité visuelle et l'acuité tactile. En effet, la vue permet généralement de
reconnaître de très petites différences de longueur entre deux objets. Cependant, il est plutôt difficile, en
soupesant deux objets, de discerner une petite différence de masse (par exemple, différence de moins de 100 g).
Le personnel enseignant doit fournir aux élèves de multiples occasions de soupeser divers objets pour les aider à
concevoir des repères de masse (par exemple, un sac de sucre a une masse de 2 kg ou de 2 000
g).
De plus, le volume d'un objet influe parfois sur la perception que l'on peut avoir de sa
masse. Ainsi, les élèves ont parfois l'impression qu'un objet de grand volume a nécessairement une plus grande masse
qu'un objet de petit volume. De même, lorsque les élèves observent deux objets de même volume, certaines et certains
ont l'impression qu'ils ont nécessairement la même masse. Il leur suffit de penser à deux boîtes de mêmes dimensions,
l'une remplie de livres et l'autre remplie d'oreillers de plumes, pour comprendre qu'il n'en est rien.
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 15.
Connaissance : repères associés à l'attribut capacité
La capacité fait référence à la quantité d'une substance qu'un emballage peut contenir. Il est parfois difficile pour
les élèves de concevoir des repères pour cet attribut, puisque la capacité d'un emballage peut s'exprimer en grammes
(par exemple, la capacité d'une boîte de céréales), en millilitres ou en litres (par exemple, la capacité d'un
contenant de jus) ou encore en centimètres cubes (par exemple, la capacité d'une boîte d'emballage). Elle peut aussi
s'exprimer en fonction du nombre d'objets identiques qu'un emballage peut contenir (par exemple, un contenant
cylindrique qui a une capacité de trois balles de tennis). De plus, puisque les liquides prennent la forme du
contenant dans lequel ils sont placés, il est difficile pour les élèves de se faire une image mentale d'une capacité
de 1 l ou de 1 ml sans tenir compte du contenant. Le personnel enseignant peut les inciter à utiliser divers
articles que l'on trouve à la maison afin de concevoir des repères pour l'attribut capacité (par exemple, un
sac de 1 l de lait, une bouteille d'eau de 500 ml, une boîte de 250 g de
biscuits).
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p.
16.
Connaissance : attribut longueur
La longueur est le terme général utilisé pour désigner toute grandeur d'un espace à une dimension que l'on mesure à
l'aide d'un étalon.
Une longueur peut désigner :
- la grandeur d'un segment, c'est-à-dire la distance entre deux points;
- la distance entre deux droites parallèles ou deux plans parallèles;
- un périmètre;
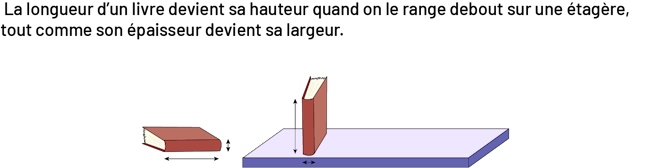
- une hauteur, une profondeur, une épaisseur, une largeur, une taille.
Note : Pour certaines et certains élèves, ces différents termes associés à la
longueur peuvent prêter à confusion.
Exemples
Image Il y a trois symboles. Le premier est composé d’un trait droit et d’un trait ondulé. Le deuxième est composé d'un ensemble de traits verticaux et d’un trait horizontal qui identifie la distance entre les traits. Le troisième est d’une clôture d’une hauteur de trois planches. Il y a un trait qui dénote la longueur des planches.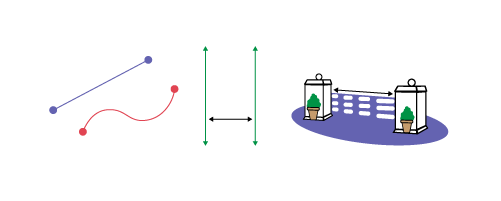
 image Il y a deux images: la première est d’un panneau d’arrêt, encerclé par
une ligne pointillée; la deuxième image est d’un bâton de beurre, dont la hauteur et la longueur sont identifiées par
une flèche verticale et horizontale respectivement.
image Il y a deux images: la première est d’un panneau d’arrêt, encerclé par
une ligne pointillée; la deuxième image est d’un bâton de beurre, dont la hauteur et la longueur sont identifiées par
une flèche verticale et horizontale respectivement.
 image
Deux images: la première est d’un livre posé horizontalement. Une ligne pointillée mesure le côté le plus long du
livre et une autre mesure l’épaisseur. La deuxième image est d’un livre posé verticalement sur une étagère. Une ligne
pointillée mesure le côté le plus long du livre et une autre mesure l’épaisseur.
image
Deux images: la première est d’un livre posé horizontalement. Une ligne pointillée mesure le côté le plus long du
livre et une autre mesure l’épaisseur. La deuxième image est d’un livre posé verticalement sur une étagère. Une ligne
pointillée mesure le côté le plus long du livre et une autre mesure l’épaisseur.
Source : Fiche de la 4e à la 6e année_Attribut longueur.
CONNAISSANCE : ATTRIBUT AIRE
L'aire désigne la grandeur d'une surface ou d'un espace à deux dimensions. L'étendue d'un terrain et la superficie d'un pays représentent aussi une mesure d'aire.
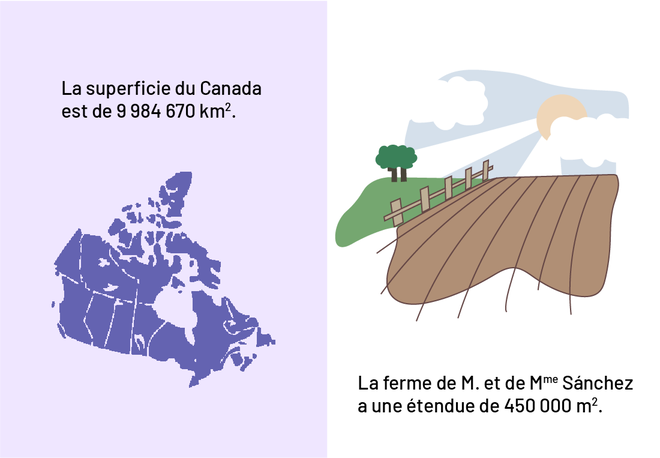 image Il y a deux illustrations. Dans la première est une mappe du
Canada. Par-dessus est écrit: la superficie du Canada est de neuf millions 984 mille 670 kilomètres carrés. Dans la
deuxième image, il y a un chantier et une clôture sous un ciel ensoleillé. Sous l’image est écrit: la ferme de
monsieur et de madame Sánchez a une étendue de 450 mille mètres carrés.
image Il y a deux illustrations. Dans la première est une mappe du
Canada. Par-dessus est écrit: la superficie du Canada est de neuf millions 984 mille 670 kilomètres carrés. Dans la
deuxième image, il y a un chantier et une clôture sous un ciel ensoleillé. Sous l’image est écrit: la ferme de
monsieur et de madame Sánchez a une étendue de 450 mille mètres carrés.
Source : Fiche de la 4e à la 6e année_Attribut aire.
Connaissance : attribut masse
La masse désigne la quantité de matière d'un objet. Seule la sorte de matière qui constitue un objet influence sa
masse. Ainsi, la masse d'un objet ne varie pas en fonction de l'endroit où il est situé sur la Terre (ou dans
l'espace).
La masse d'un objet est déterminée à l'aide, par exemple, d'une balance à triple fléau ou
d'une balance à deux plateaux.
Note : Il ne faut pas confondre masse et poids. Le poids d'un objet désigne la force qu'exerce un corps céleste sur cet objet. Il est déterminé à l'aide d'un dynamomètre et il est exprimé en newtons (N). Le poids d'un objet varie selon sa masse et selon l'endroit où il est situé sur la Terre (ou dans l'espace).
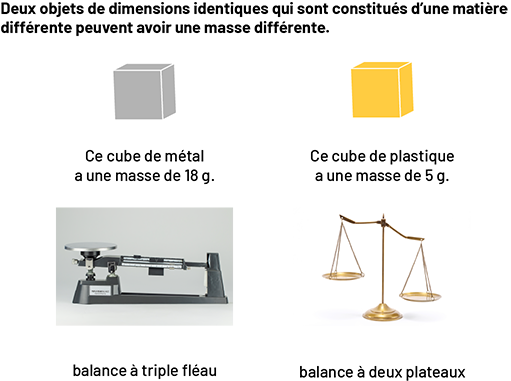 image Il y a quatre images, par-dessus lesquels est écrit: deux objets de dimensions identiques qui
sont constitués d’une matière différente peuvent avoir une masse différente. La première image est d’un cube de
matière, la deuxième d’un cube de plastic, la troisième d’une balance à triple fléau, et la quatrième d’une balance à
doubles plateaux. Sous le premier cube est écrit: ce cube de matière a une masse de 18 grammes. Sous le deuxième cube
est écrit: ce cube de plastique a une masse de cinq grammes. Sous la première balance est écrit: balance à triple
fléau. Sous la deuxième balance est écrit: balance à doubles plateaux.
image Il y a quatre images, par-dessus lesquels est écrit: deux objets de dimensions identiques qui
sont constitués d’une matière différente peuvent avoir une masse différente. La première image est d’un cube de
matière, la deuxième d’un cube de plastic, la troisième d’une balance à triple fléau, et la quatrième d’une balance à
doubles plateaux. Sous le premier cube est écrit: ce cube de matière a une masse de 18 grammes. Sous le deuxième cube
est écrit: ce cube de plastique a une masse de cinq grammes. Sous la première balance est écrit: balance à triple
fléau. Sous la deuxième balance est écrit: balance à doubles plateaux.
Source : Fiche de la
4e à la 6e année_Attribut masse.
Connaissance : attribut capacité
La capacité d'un contenant désigne la quantité maximale d'une substance donnée qu'il est possible de mettre à l'intérieur du contenant. Lorsque la substance donnée remplit complètement le contenant, la capacité équivaut au volume intérieur du contenant.
 image Trois images: Un poisson dans un aquarium; un cylindre contenant trois
balles de tennis et un cylindre rempli d’eau; et une boîte en carton. À côté de l’image de l’aquarium est écrit: la
capacité ou le volume de cet aquarium est de deux litres. À côté de l’image, des cylindres est écrit: ce cylindre a
une capacité de trois balles de tennis et un volume intérieur de 750 millilitres. À côté de l’image de la boîte en
carton est écrit: Cette boîte a une capacité ou un volume intérieur de mille 200 centimètres cubes.
image Trois images: Un poisson dans un aquarium; un cylindre contenant trois
balles de tennis et un cylindre rempli d’eau; et une boîte en carton. À côté de l’image de l’aquarium est écrit: la
capacité ou le volume de cet aquarium est de deux litres. À côté de l’image, des cylindres est écrit: ce cylindre a
une capacité de trois balles de tennis et un volume intérieur de 750 millilitres. À côté de l’image de la boîte en
carton est écrit: Cette boîte a une capacité ou un volume intérieur de mille 200 centimètres cubes.
