E2.4 Expliquer le fonctionnement d'un rapporteur d'angles et l'utiliser pour mesurer et construire des angles jusqu'à 180°, et se servir d'angles repères pour estimer la taille d'autres angles.
HABILETÉ : EXPLIQUER LE FONCTIONNEMENT D'UN RAPPORTEUR
Les élèves apprennent à estimer des mesures d'angles en degrés et à déterminer ces mesures à l'aide d'un rapporteur. Au début, bien des élèves ont de la difficulté à placer correctement le rapporteur sur l'angle qu'elles et ils veulent mesurer et à utiliser la bonne graduation pour lire la mesure. Il est essentiel d'offrir aux élèves une variété d'activités qui nécessitent l'utilisation d'un rapporteur afin de les aider à développer cette habileté (par exemple, construire des angles et des triangles de mesures données).
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 27.
Ce n'est que lorsque l'élève aura eu de nombreuses expériences qui l'auront mené à identifier des angles, à les comparer et à les mesurer à l'aide de mesures non conventionnelles et de repères qu'elle ou il sera prête ou prêt à construire divers types de triangles à l'aide d'outils tels le goniomètre et le rapporteur. Ce dernier est un outil qui crée la confusion chez plusieurs élèves du cycle moyen. En effet, les unités de mesure sont écrites en très petits caractères et la plupart des rapporteurs présentent deux séries de chiffres. Il serait préférable que les élèves s'exercent à l'aide d'un rapporteur de leur fabrication qui indique des unités de mesure plus grandes pour apprendre à bien l'utiliser. Les élèves pourraient, par exemple, se construire un rapporteur transparent, en pliant un morceau de papier ciré, et mesurer les angles en comptant le nombre de pointes.
Après de nombreuses expériences en utilisant le rapporteur de leur fabrication, les élèves peuvent comparer celui-ci à un rapporteur conventionnel pour mieux en comprendre le fonctionnement.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 19-20.
En 5e année, les élèves doivent connaître les parties d'un rapporteur, soit la ligne de foi et le point d'origine.
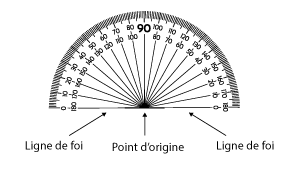
Pour mesurer un angle à l'aide d'un rapporteur, les élèves doivent aligner le point d'origine du rapporteur sur le sommet de l'angle. Elles et ils doivent ensuite aligner la ligne de foi du rapporteur sur un des segments. Puis, elles et ils peuvent lire la mesure de l'angle dans le sens horaire ou anti-horaire, selon la position de l'angle.
Source : En avant, les maths! 5e année, CM, SDE, p. 3.
HABILETÉ : UTILISER UN RAPPORTEUR POUR MESURER DES ANGLES JUSQU'À 180°
Au moment d'utiliser un rapporteur, il est important de respecter les consignes suivantes.
- S'assurer qu'au moins un côté de l'angle dépasse le rapporteur.
Si les segments de droite qui forment l'angle sont trop courts pour la taille du rapporteur, il faut les allonger. Il faut utiliser une règle pour faire des lignes bien droites en prolongeant les côtés de l'angle. - Estimer la mesure de l'angle.
Observer l'angle pour déterminer si c'est un angle aigu ou obtus. Ensuite, en déduire une mesure approximative qui servira à choisir l'échelle sur le rapporteur et à vérifier la vraisemblance de la mesure finale. - Placer la ligne de foi sur le côté initial de l'angle.
Choisir un côté qui sera le côté initial. Superposer la ligne de foi au côté initial. Faire coïncider le point d'origine avec le sommet de l'angle. - Lire la mesure qui coïncide avec le deuxième côté de l'angle, soit au point d'intersection du segment et du rapporteur.
- Vérifier la mesure avec l'estimation.
- S'assurer que la mesure trouvée correspond à l'estimation du début.
Très important!
Lorsque les élèves observent la représentation d'un angle, elles et ils doivent porter leur attention sur l'amplitude de l'inclinaison entre les deux segments de droite et non sur les segments eux-mêmes. C'est le secteur angulaire qui est mesuré. La longueur des segments de droite n'a aucune influence sur la mesure de l'angle.
Source : L'@telier - Ressources pédagogiques en ligne (atelier.on.ca).
Exemple
Je place le point d'origine du rapporteur sur le sommet E de l'angle DEF. J'aligne la ligne de foi du rapporteur sur segment DE. Je fais la lecture dans le sens des aiguilles d'une montre en partant du point D, 0°, jusqu'au point F. Je lis la mesure qui coïncide avec le segment EF, soit 120°.
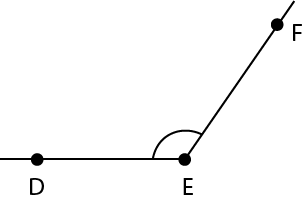
Source : En avant, les maths!, 5e année, CM, Sens de l'espace, p. 11.
Introduction à la mesure d'un angle
La page Web d'activités Introduction à la mesure d'un angle (atelier.on.ca) comporte des vidéos explicatives permettant de comprendre la façon de mesurer un angle à l'aide d'un rapporteur et d'un goniomètre, et la manière de vérifier la congruence de deux angles.
Enseigner le concept d'angle, la façon de le mesurer et la roulette des angles
La page Web d'activités Enseigner le concept d'angle et comment le mesurer (atelier.on.ca) comprend des explications et des vidéos portant sur le concept de mesure d'un angle, la roulette des angles et l'estimation d'un angle, ainsi qu'un jeu.
HABILETÉ : UTILISER UN RAPPORTEUR POUR CONSTRUIRE DES ANGLES JUSQU'À 180°
Construire un angle
La page Web d'activités Construire un angle (atelier.on.ca) comprend des vidéos explicatives montrant la façon de construire un angle à l'aide d'un rapporteur et d'un goniomètre.
HABILETÉ : SE SERVIR D'ANGLES REPÈRES POUR ESTIMER LA TAILLE D'AUTRES ANGLES
Au cycle moyen, les élèves doivent apprendre à utiliser diverses stratégies pour effectuer des estimations dans des situations de plus en plus complexes en utilisant à la fois des unités de mesure non conventionnelles et conventionnelles. Il importe donc que le personnel enseignant planifie des interventions et un enseignement formel axé sur des stratégies d'estimation particulières. Van de Walle et Lovin proposent l'enseignement de stratégies d'estimation. Une de celle-ci se réfère à l’utilisation de repères.
|
Stratégie |
Exemple |
|
Développer et utiliser des repères qui représentent des unités de mesure importantes. Les élèves qui se sont constituées et constitués un répertoire de repères et qui les utilisent régulièrement réussissent à estimer avec plus d'efficacité et d'aisance. L'estimation de la mesure de l'attribut se fait en le comparant à un repère. |
Pour estimer la mesure d'un angle donné, les élèves peuvent utiliser l'angle droit et l'angle plat comme repères. En superposant mentalement l'image de ces angles sur l'angle donné, elles et ils peuvent conclure que sa mesure est beaucoup plus près de 90°que de 180°. Elles et ils estiment alors que la mesure de l'angle donné est d'environ 100°. 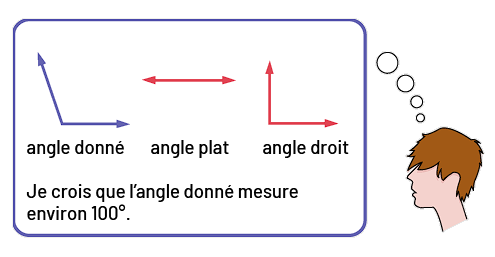 image Dans un rectangle arrondi se trouvent trois angles: soit un angle donné qui est formé
d’une courte ligne verticale et d’une courte ligne diagonale vers la gauche, un angle plat, et un angle droit.
Au bas du rectangle est écrit: je crois que l’angle donné mesure environ cent degrés. À l’extérieur du
rectangle, il y a un personnage.
|
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 18-19.
Exemples – Estimation de mesures d'angles et comparaison d'angles à l'aide d'angles repères
Je sais qu'un angle droit mesure 90°. Je sais aussi qu'un carré a quatre angles droits. Alors, j'utilise
une mosaïque géométrique orange en forme de carré afin de déterminer si l'angle est plus grand, plus petit ou égal à
90°, ainsi que pour m'aider à estimer sa mesure. À l'aide du carré, je peux également avoir des angles repères autres
que celui de 90°.
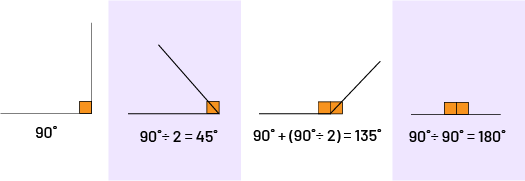image Il y a quatre angles différents. Les deux premiers ont une mosaïque
géométrique en forme de carre dans le coin. Les deux derniers ont deux mosaïques géométriques en forme de carre dans
le coin. Sous le premier ange est écrit: 90 degrés. Sous le deuxième angle est écrit: 90 degrés divisés par deux
égales à 45 degrés. Sous le troisième angle est écrit: 90 degrés plus (parenthèse ouvrante) 90 degrés divisés par deux
(parenthèse fermante) égale à 135 degrés. Sous la quatrième image est écrit: 90 degrés plus 90 degrés égale à 180
degrés.
J'utilise des angles connus pour estimer les mesures des angles. Je sais qu'une mosaïque géométrique, soit le
losange beige, a un angle de 30°. Je superpose l'angle de la pointe du losange sur les angles pour m'aider à les
estimer.
L'angle DEF est un angle obtus. J'estime sa mesure à 120°, car il correspond à environ 4 × 30° ou à 30° + 30° + 30° + 30° = 120°.
Source : En avant, les maths!, 5e année, CM, Sens de l'espace, p. 5-7.