E2.6 Démontrer que des figures planes ayant la même aire peuvent avoir des périmètres différents et résoudre des problèmes connexes.
HABILETÉ : DÉMONTRER QUE DES FIGURES PLANES AYANT LA MÊME AIRE PEUVENT AVOIR DES PÉRIMÈTRES DIFFÉRENTS
Relations entre des attributs
L'exploration des relations entre des attributs permet aux élèves de développer une meilleure compréhension des formules usuelles utilisées pour déterminer l'aire de certaines figures planes ou le volume de certains solides, et de les appliquer en toute connaissance de cause dans diverses situations de résolution de problèmes.
Relations entre les attributs longueur et aire
Le personnel enseignant doit présenter aux élèves des activités de mesure leur permettant d'établir une relation entre les dimensions (base et hauteur) de certaines figures planes (rectangle, parallélogramme et triangle) et leur aire. Les élèves doivent construire les concepts de « hauteur » et de « base » par l'intermédiaire d'activités qui les aident à comprendre que n'importe lequel des côtés d'une figure peut être la base et que, pour chaque base, il y a une « hauteur » correspondante.
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 70.
Le personnel enseignant peut aussi proposer aux élèves des activités qui leur permettent d'explorer des situations pour lesquelles il n'y a pas de relation entre les attributs longueur et aire. Ce type d'activité aide les élèves à mieux comprendre l'importance de vérifier une conjecture avant de conclure qu'elle est vraie.
Exemple 1
Le personnel enseignant demande aux élèves s'il y a, selon elles et eux, une relation entre le périmètre de deux
figures planes qui ont la même aire. Une ou un élève dit : « Je pense que si deux figures planes ont la même
aire, elles ont aussi le même périmètre. » Le personnel enseignant demande aux autres élèves si elles et ils
pensent que cette conjecture est vraie ou si elles et ils pensent qu'elle est fausse. Elle ou il groupe ensuite les
élèves en équipes de deux et leur suggère de vérifier la conjecture.
Pour ce faire, le personnel enseignant propose aux élèves la marche à suivre ci-après :
- tracer deux carrés identiques;
- déterminer l'aire et le périmètre des carrés;
- tracer une diagonale dans un des deux carrés et découper ce carré de façon à obtenir deux triangles;
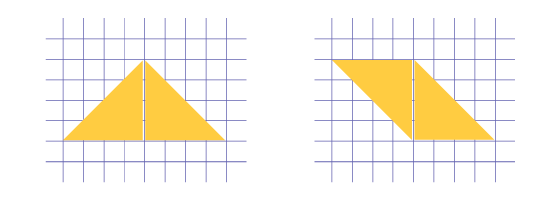
- former de nouvelles figures planes à l'aide de ces deux triangles et déterminer le périmètre de chacune;
- utiliser les résultats pour déterminer si la conjecture est vraie ou fausse.
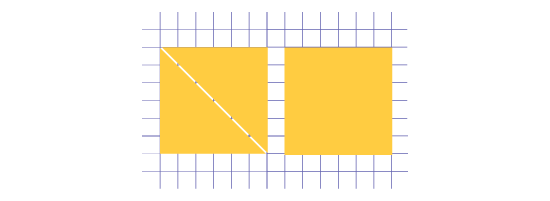
Les photos ci-dessous montrent deux figures qui pourraient être formées en se servant des triangles. À l'aide de ces figures, les élèves peuvent constater que même si l'aire de chacune des figures est égale à l'aire du carré original, la mesure de leur périmètre est différente. Elles et ils peuvent alors conclure que la conjecture est fausse, c'est-à-dire que si deux figures planes ont la même aire, elles n'ont pas nécessairement le même périmètre.
Exemple 2
Le personnel enseignant demande aux élèves s'il y a, selon lui, une relation entre l'aire de deux figures planes qui
ont le même périmètre. Une ou un élève dit : « Je pense que même si deux figures planes ont le même
périmètre, elles n'ont pas nécessairement la même aire. » Le personnel enseignant demande aux autres élèves si
elles et ils pensent que cette conjecture est vraie ou si elles et ils pensent qu'elle est fausse. Elle ou il groupe
ensuite les élèves en équipes de deux et leur suggère de vérifier la conjecture.
Pour ce faire, le
personnel enseignant leur propose la marche à suivre ci-après :
- tracer sur du papier quadrillé divers rectangles qui ont un périmètre de 16 cm;
- déterminer l'aire de chacun des rectangles;
- utiliser les résultats pour indiquer si la conjecture est vraie ou fausse.
La figure ci-dessous illustre quelques rectangles qui pourraient être tracés. À l'aide de ces rectangles, les élèves peuvent constater que même si les rectangles ont le même périmètre (16 cm), ils n'ont pas la même aire. Elles et ils sont alors en mesure de conclure que la conjecture est vraie, c'est-à-dire que si deux figures planes ont le même périmètre, elles n'ont pas nécessairement la même aire.
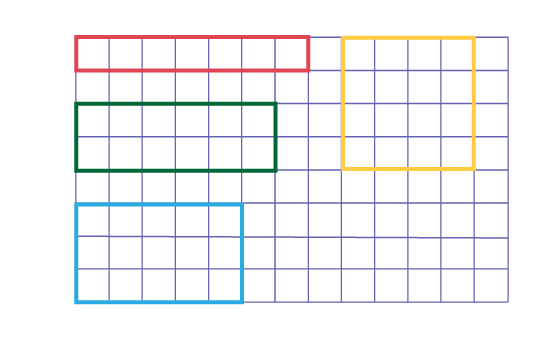
Note : Le personnel enseignant peut inciter les élèves à pousser leur réflexion plus loin et à
constater que, dans le cas de rectangles de même périmètre, celui dont l'aire est la plus grande est le
carré.
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 77-79.
