E1.1 Créer des listes des propriétés géométriques de divers types de quadrilatères, y compris les propriétés des diagonales, la symétrie rotationnelle et les axes de symétrie.
ACTIVITÉ 1 : PROPRIÉTÉS COMMUNES ET DISTINCTES DES QUADRILATÈRES
La leçon se déroulera en trois étapes distinctes soit :
Étape 1 : Avant (mise en situation)
Le personnel enseignant fait un retour sur les quadrilatères connus : carré, rectangle, losange, parallélogramme.
Étape 2 : Pendant (exploration)
Le personnel enseignant présente trois nouveaux quadrilatères : trapèze, cerf-volant, deltoïde. Il demande ensuite aux élèves de classer les quadrilatères selon certaines propriétés.
Étape 3 : Après (objectivation/transfert de connaissances)
Les élèves découvrent que les quadrilatères ont des ressemblances et des différences et que certains possèdent des propriétés communes.
Source : L’@telier - Ressources pédagogiques en ligne (atelier.on.ca).
ACTIVITÉ 2 : EST-CE POSSIBLE?
Cette activité intègre des concepts de raisonnement géométrique et spatial, du sens de la mesure et du domaine Données (Probabilité).
Le personnel enseignant formule un énoncé lié aux propriétés des formes géométriques, qui présente une situation certaine, probable ou impossible. Par exemple, il dit : « Ma pyramide a une base carrée. » Les élèves doivent utiliser leurs connaissances des propriétés des formes géométriques pour indiquer si c’est certain, probable ou impossible, et pour justifier leur réponse. Dans cet exemple, une ou un élève pourrait répondre que c’est probable, car la pyramide pourrait non seulement avoir une base carrée, mais aussi une base triangulaire, pentagonale, hexagonale, etc. Le personnel enseignant leur demande ensuite de modifier l’énoncé afin qu’il présente une situation certaine ou impossible. Par exemple, une ou un élève pourrait dire « ma pyramide a une base » (situation certaine) ou « ma pyramide n’a aucune base » (situation impossible).
Autres exemples d’énoncés :
- « Mon hexagone a six côtés. » Cet énoncé représente une situation certaine, car tous les hexagones ont six côtés.
- « Mon rectangle a un angle de 45° ». Cet énoncé représente une situation impossible, car tous les rectangles ont quatre angles de 90°.
- « Mon angle aigu mesure 120° ». Cet énoncé représente une situation impossible, car tous les angles aigus mesurent moins de 90°.
Après avoir formé des équipes de deux élèves, le personnel enseignant leur demande d’écrire des énoncés semblables à ceux qu’il leur a présentés et qui ont un lien avec des formes géométriques qu’elles et ils connaissent. Tour à tour, une ou un élève lit un de ses énoncés. L’autre précise, avec justifications à l’appui, si l’énoncé représente une situation certaine, probable ou impossible. Par la suite, il modifie l’énoncé pour qu’il représente l’une ou l’autre des deux autres situations. L’élève qui a lu l’énoncé initial doit à son tour préciser la situation qui est représentée par ce nouvel énoncé.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 42.
ACTIVITÉ 3 : MON CASSE-TÊTE
Demander aux élèves de créer, à l’aide d’un logiciel ou d’une application de géométrie dynamique, un casse-tête rectangulaire symétrique en utilisant les polygones de leur choix, puis de dresser une liste de critères qui pourraient définir la construction du casse-tête. Une fois ce travail terminé, leur demander d’échanger leur liste avec une ou un autre élève et de tenter de construire un casse-tête qui est conforme à cette liste.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 77.
ACTIVITÉ INTERACTIVE 4 : QUADRILATÈRES
Sommaire
Dans cette activité, les élèves font l’apprentissage des propriétés des quadrilatères.
Source : L’@telier - Ressources pédagogiques en ligne (atelier.on.ca).
ACTIVITÉ INTERACTIVE 5 : TROUVE LA FIGURE GÉOMÉTRIQUE
Sommaire
Dans cette activité, les élèves lisent les propriétés géométriques et sélectionnent la figure géométrique qui possède
cette propriété.
Source : L'@telier - Ressources pédagogiques en ligne (atelier.on.ca).
ACTIVITÉ 6 : CONSTRUCTION DE QUADRILATÈRES À L’AIDE D’UN LOGICIEL OU D’UNE APPLICATION DE GÉOMÉTRIE DYNAMIQUE
En réalisant des activités à l’aide de la technologie, les élèves sont en mesure d’analyser plus facilement de nombreux cas, de vérifier des hypothèses et d’établir des conjectures. L’utilisation de logiciels ou d’applications de géométrie dynamique les aide à explorer plus facilement divers cas à l’intérieur même d’une classe de formes géométriques. En effet, les élèves dessinent des objets géométriques, puis les déplacent et les transforment de nombreuses façons. Ainsi, elles et ils examinent une forme géométrique, mais également un nombre important d’exemples faisant partie d’une même classe de figures. Lorsqu’une propriété d’une forme géométrique est conservée à la suite d’une transformation, c’est qu’il s’agit d’une caractéristique de la forme géométrique et qu’en plus elle suffit pour décrire une classe entière de formes géométriques.
Le personnel enseignant peut, par exemple, demander à des élèves de nommer des quadrilatères différents ayant comme propriété des diagonales qui se coupent en leur milieu. À l’aide d’un logiciel ou d’une application de géométrie dynamique, les élèves créent un premier quadrilatère dont deux des sommets sont les extrémités d’un segment de droite et dont les deux autres sommets sont des points sur un cercle qui partage son centre avec le point milieu du segment. Les fonctionnalités du logiciel ou de l’application font en sorte qu’il est facile de mesurer des longueurs ou des angles. À partir de ces mesures, les élèves peuvent justifier le nombre de quadrilatères différents pouvant être formés.
Voici des exemples de quadrilatères obtenus à l’aide d’un logiciel de géométrie dynamique :
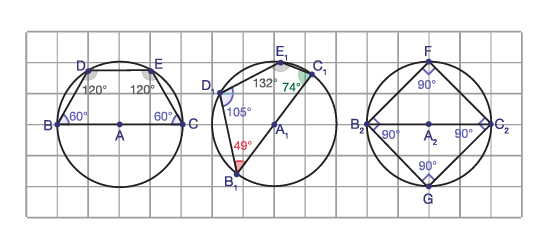 Image Il
y a une grille sur laquelle se trouvent trois cercles. Dans les cercles sont trois quadrilatères différents: le
premier a deux angles de 120 degrés et deux angles de 60 degrés; le deuxième a un angle de 105 degrés, un angle de 132
degrés, un angle de 74 degrés, et un angle de 49 degrés; le troisième a quatre angles de 90 degrés.
Image Il
y a une grille sur laquelle se trouvent trois cercles. Dans les cercles sont trois quadrilatères différents: le
premier a deux angles de 120 degrés et deux angles de 60 degrés; le deuxième a un angle de 105 degrés, un angle de 132
degrés, un angle de 74 degrés, et un angle de 49 degrés; le troisième a quatre angles de 90 degrés.
Source : Guide d’enseignement efficace des mathématiques, de la 7e à la 10e année, p. 27.
ACTIVITÉ 7 : QUADRILATÈRES
Distribuer aux élèves un ensemble de quadrilatères et leur demander d’en dessiner en utilisant un logiciel ou une application de géométrie dynamique. Leur distribuer également le tableau des observations ou téléverser un document sur une plateforme Web afin qu’elles et ils puissent y consigner leurs observations.

Tableau des observations
|
Figure |
Nom et caractéristiques |
Diagonale |
Milieux des côtés |
| 1 | |||
| 2 | |||
| 3 | |||
| 4 | |||
| 5 | |||
| 6 | |||
| 7 | |||
| 8 | |||
| 9 |
Étape 1
Demander aux élèves d’observer les quadrilatères, d’en déterminer les caractéristiques, puis de remplir la première colonne du tableau des observations.
Les élèves devraient être en mesure de reconnaître les types de quadrilatères (parallélogramme, trapèze rectangle, trapèze isocèle, carré, losange, chevron, cerf-volant, quadrilatères quelconques) ainsi que leurs caractéristiques (côtés égaux, côtés parallèles, côtés perpendiculaires, angles congrus).
Inviter les élèves à vérifier si leurs observations relatives à un quadrilatère s’appliquent à d’autres quadrilatères semblables. Par exemple, leur demander :
- de vérifier si les mêmes caractéristiques s’appliquent à d’autres quadrilatères;
- de dessiner un quadrilatère qui a quatre côtés égaux, mais aucun angle droit.
Étape 2
À cette étape-ci, selon les critères définis par van Hiele, les élèves ont un niveau de pensée en géométrie de niveau
1, soit l’analyse. L’activité qui suit relève de ce niveau.
Demander aux élèves de tracer les diagonales
des quadrilatères en utilisant du matériel de manipulation ou un logiciel ou une application de géométrie dynamique,
puis d’écrire leurs observations dans la deuxième colonne du tableau. L’exploration des diagonales des quadrilatères
peut se faire à l’aide de bandes de papier trouées et d’attaches parisiennes ou avec des bâtonnets en plastique, comme
les GeoStix. Les bandes de papier représentent les diagonales pouvant être croisées de différentes façons et fixées à
l’aide d’attaches parisiennes. Ainsi, les élèves pensent aux propriétés et aux caractéristiques propres aux formes
géométriques qu’il est possible de créer lorsque deux segments se croisent. En explorant divers croisements de
segments, cela les aide à reconnaître des classes de figures. Elles et ils peuvent ainsi regrouper des figures en une
classe, soit les quadrilatères, en fonction de la longueur de leurs diagonales, du rapport entre les parties de ces
diagonales et de la présence ou non d’un angle de 90 degrés.
 Image Il
y a quatre images. Dans la première, il y a deux bandes de papier trouées formant deux formes de « x ». Dans la
deuxième image, il y a deux symboles plus et deux « x » sur un plan cartésien. Dans la troisième image, il y a deux
symboles plus est un « x ». Dans la quatrième image, il y a trois quadrilatères marqués par un symbole plus ou un « x
».
Image Il
y a quatre images. Dans la première, il y a deux bandes de papier trouées formant deux formes de « x ». Dans la
deuxième image, il y a deux symboles plus et deux « x » sur un plan cartésien. Dans la troisième image, il y a deux
symboles plus est un « x ». Dans la quatrième image, il y a trois quadrilatères marqués par un symbole plus ou un « x
».
Inviter les élèves à explorer la façon dont se coupent les diagonales des différents quadrilatères ainsi que l’endroit où elles se coupent; par exemple :
- Y a-t-il plusieurs quadrilatères dont les diagonales se coupent en leur milieu?
- Y a-t-il des quadrilatères dont les diagonales se coupent à un angle de 90°?
Étape 3
Demander aux élèves de joindre les milieux des côtés de chaque figure de manière à former un autre quadrilatère et d’écrire leurs observations dans la dernière colonne du tableau.
Étape 4
Demander aux élèves d’utiliser un logiciel ou une application de géométrie dynamique, de formuler des hypothèses à la suite de leurs observations, de tirer des conclusions et de faire des généralisations.
Dans l’exemple ci-dessous, la figure ABCD est un carré et la figure intérieure est aussi un carré ou un parallélogramme. Si le sommet C est déplacé horizontalement vers la droite, la figure obtenue est un trapèze rectangle et la figure intérieure est encore un parallélogramme.
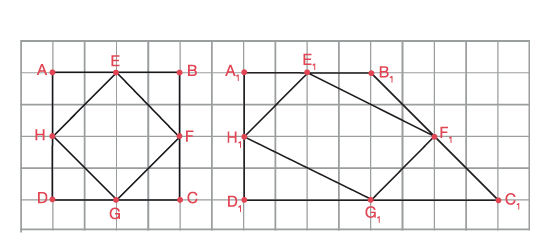
Dans l’exemple ci-dessous, la figure ABCD est un parallélogramme et la figure HEFG est aussi un parallélogramme. Si le sommet C est déplacé vers la droite et vers le bas, la figure obtenue est un quadrilatère quelconque et la figure intérieure est également un parallélogramme.
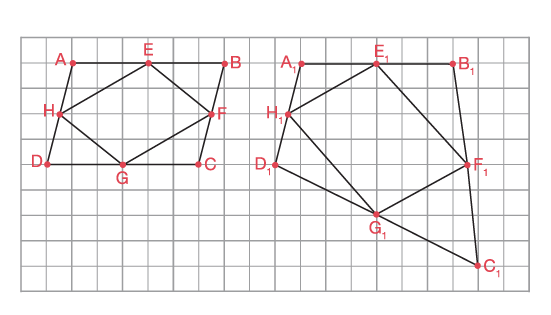
Dans l’exemple ci-dessous, la figure ADFB est un quadrilatère convexe et la figure CEGH est un parallélogramme. Si le sommet D est déplacé vers la droite et vers le bas, la figure obtenue est un autre quadrilatère convexe et la figure intérieure obtenue est encore un parallélogramme.
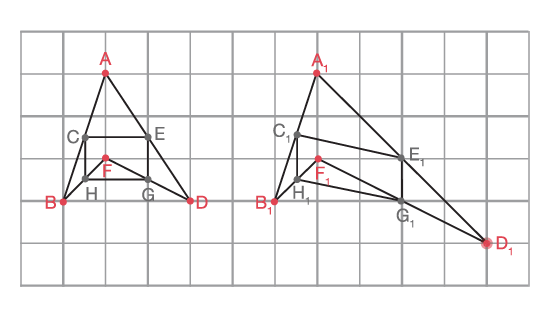
Inviter les élèves à explorer différentes méthodes pour démontrer la même hypothèse; par exemple :
- Comment pouvez-vous démontrer, à l’aide de la géométrie, que si deux diagonales d’un quadrilatère se coupent en leur milieu, alors il s’agit d’un parallélogramme?
- Comment pouvez-vous démontrer, à l’aide de la géométrie, que la figure qui relie les milieux des côtés d’un trapèze isocèle est toujours un parallélogramme?
Source : Guide d’enseignement efficace des mathématiques, de la 7e à la 10e année, p. 28-31.
