E1.2 Construire des objets à trois dimensions à partir de vues de face, de côté et de dessus.
Activité 1 : LES OBJETS ET LEUR FORME
Cette activité intègre des concepts du domaine Sens de l’espace et des concepts de sciences et de technologie.
Afin de promouvoir le développement d’habiletés en recherche scientifique et en design, le personnel enseignant propose aux élèves d’analyser un objet usuel en mettant l’accent sur les propriétés liées à sa forme. Par exemple, il peut demander aux élèves :
- de se représenter un objet quelconque qui a une forme différente de la forme traditionnelle et de discuter de ses avantages et de ses désavantages (par exemple, une porte qui n’est pas rectangulaire, un ballon qui n’est pas sphérique, un toit qui n’est pas triangulaire);
- de recenser les diverses formes que prend un objet et de faire ressortir les avantages et les désavantages de chacune (par exemple, diverses formes d’ampoules électriques).
Divers objets peuvent ainsi être étudiés en accordant une attention particulière à leur forme (par exemple, avion, fusée, parachute, montgolfière, disque volant, cerf-volant, sablier). Le personnel enseignant forme des équipes de deux élèves. Chaque équipe doit effectuer une recherche (par exemple, à la bibliothèque, dans Internet) et construire un prototype d’un objet en utilisant une forme géométrique non traditionnelle. Les élèves doivent ensuite présenter leur objet à la classe et en faire ressortir les avantages et les désavantages, plus particulièrement ceux liés à sa forme (par exemple, malléabilité, résonance, solidité, capacité, aérodynamisme, esthétique). Au moment de la construction du prototype, il importe cependant que les élèves ne mettent pas l’accent uniquement sur l’aspect esthétique de l’objet.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 44-45.
ACTIVITÉ 2 : MYSTÉRIEUSES RUINES
Distribuer aux élèves les diverses vues d’un monument suivantes.
 Image La vue d’un monument, de deux perspectives représentées en carrés. Au-dessus de la première
figure est écrit: vue du côté est. Au-dessus de la seconde figure est écrit: vue du côté ouest. En haut, il est écrit:
Monument (parenthèse ouvrante) vue des côtés est et ouest (parenthèse fermante).
Image La vue d’un monument, de deux perspectives représentées en carrés. Au-dessus de la première
figure est écrit: vue du côté est. Au-dessus de la seconde figure est écrit: vue du côté ouest. En haut, il est écrit:
Monument (parenthèse ouvrante) vue des côtés est et ouest (parenthèse fermante).
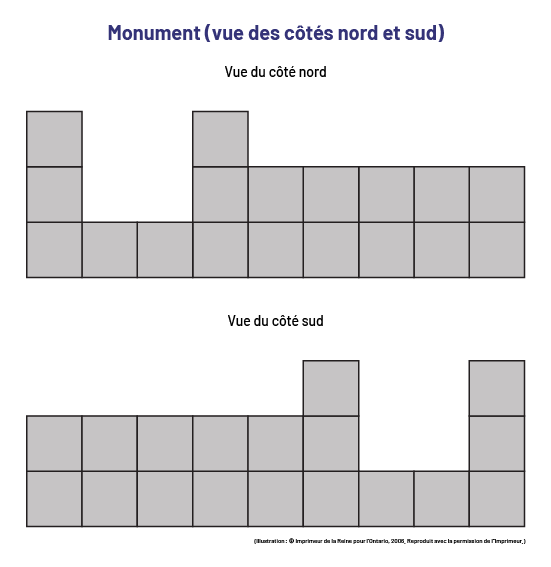 Image La vue d’un monument, de deux perspectives représentées en carrés. Au-dessus de la première
figure est écrit: vue du côté nord. Au-dessus de la première figure est écrit: vue du côté sud. En haut, il est écrit:
Monument (parenthèse ouvrante) vue des côtés nord et sud (parenthèse fermante).
Image La vue d’un monument, de deux perspectives représentées en carrés. Au-dessus de la première
figure est écrit: vue du côté nord. Au-dessus de la première figure est écrit: vue du côté sud. En haut, il est écrit:
Monument (parenthèse ouvrante) vue des côtés nord et sud (parenthèse fermante).  Image Il
y a une photo d’un ancien monument en ruine. À la gauche est écrit: Sue le site archéologique, une équipe de fouilles
a mis au jour les ruines d’un très ancien monument. Afin que les archéologues puissent le reconstituer, un des
fouilleurs a tracé les vues de chacun des quatre côtés (parenthèse ouvrante) est, ouest, nord, et sud (parenthèse
fermante).
Image Il
y a une photo d’un ancien monument en ruine. À la gauche est écrit: Sue le site archéologique, une équipe de fouilles
a mis au jour les ruines d’un très ancien monument. Afin que les archéologues puissent le reconstituer, un des
fouilleurs a tracé les vues de chacun des quatre côtés (parenthèse ouvrante) est, ouest, nord, et sud (parenthèse
fermante).
Les archéologues veulent faire une maquette des ruines de ce monument avec des cubes d’après les quatre vues que le fouilleur a tracées. Elles et ils se rendent compte qu’il y a plusieurs dispositions possibles des cubes qui respectent les vues.
Pouvez-vous, à l’aide de cubes emboîtables, construire une maquette de l’une de ces dispositions? Pouvez-vous en construire une avec le moins de cubes possible?
Habiletés à développer relatives à la visualisation spatiale (voir Fondements généraux) :
- Coordination oculomotrice
- Perception des positions
- Perception des relations spatiales
Source : Guide d’enseignement efficace des mathématiques, de la 7e à la 10e année, p. 15.
ACTIVITÉ 3 : TROIS VUES VALENT MIEUX QUE DEUX
Former des équipes de deux élèves. Leur demander de construire une maquette quelconque avec un nombre donné de cubes emboîtables (par exemple, 15 cubes) et de tracer les vues de face, de côté et de dessus de cette maquette. Regrouper ensuite les équipes deux à deux et les identifier (par exemple, équipes A et B). Donner les explications suivantes :
L’équipe A donne d’abord à l’équipe B deux vues de sa maquette, soit la vue de dessus et la vue de côté ou de face.
L’équipe B doit construire une maquette qui respecte ces vues tout en utilisant tous les cubes. L’équipe A remet
ensuite la troisième vue à l’équipe B et lui demande de voir si, avec cette nouvelle information, elle doit changer
l’emplacement de certains cubes. Par la suite, l’équipe B compare sa maquette finale avec celle de l’équipe A et les
élèves discutent des ressemblances et des différences. C’est ensuite au tour de l’équipe A de tenter de reproduire la
maquette de l’équipe B en suivant la même démarche.
Note : Même avec trois vues, il est possible de construire deux maquettes qui ne sont pas parfaitement
identiques.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 92.
