E2.4 Déterminer l’aire de trapèzes, de losanges, de cerfs-volants ainsi que de polygones complexes en les décomposant en figures planes avec des aires connues.
ACTIVITÉ 1 : ACTIVITÉS DE GÉNÉRALISATION POUR L’AIRE – FIGURES DONT L’AIRE EST DONNÉE
But
Cette activité aide les élèves à consolider leur compréhension de la mesure d’aire d’une surface.
Matériel
- géoplan 11 sur 11 (un par élève)
- papier géoplan (voir l’annexe Papier géoplan)
- grille quadrillée de 1 cm sur 1 cm (voir l’annexe Grille quadrillée)
- règle graduée en centimètres
- annexe 4 et annexe 5
Déroulement
À l’aide d’un géoplan, d’une grille quadrillée ou d’une règle, construire chacune des figures ci-dessous ayant une
aire donnée. Reproduire les figures dans le cahier de notes.
- Un rectangle dont l’aire est de 20 unités carrées.
- Un carré dont l’aire est de 36 unités carrées.
- Un parallélogramme dont l’aire est de 16 unités carrées.
- Un triangle dont l’aire est de 24 unités carrées.
- Un trapèze dont l’aire est de 15 unités carrées.
Source : L'@telier - Ressources pédagogiques en ligne (atelier.on.ca), p. 8
ACTIVITÉ 2 : RELATIONS ENTRE DIVERSES FORMULES D’AIRE
Cette activité est axée sur les contenus relatifs à la découverte de formules et à l’établissement de relations entre les diverses formules d’aire.
Demander aux élèves de déterminer l’aire d’une nouvelle figure plane telle que le trapèze.
L’élève 1 visualise le trapèze comme un rectangle et deux triangles.
L’élève 2 visualise le trapèze comme un parallélogramme et un triangle.
L’élève 3 visualise le trapèze comme deux triangles.
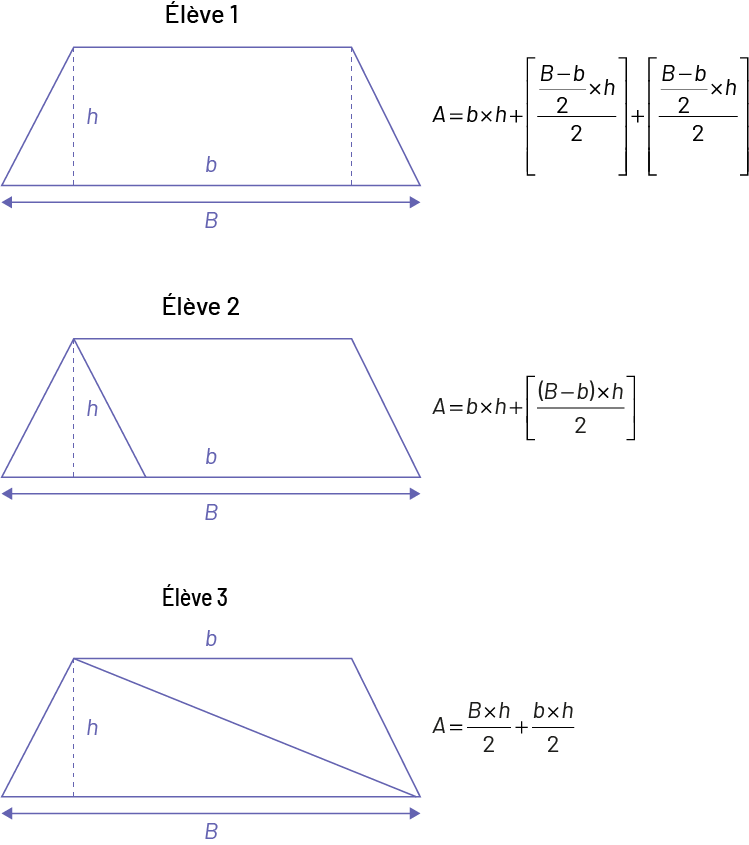Image Élève un : Un trapèze, dont la base est nommée « b » majuscule, est divisé en 3 parties.
Deux lignes
pointillées sont tracées, elles représentent la hauteur « h »; cela forme les 2 triangles. Le rectangle a la largeur
« h » et la longueur « b ». « A » égal, « b » multiplié par « h », plus [crochet ouvrant] « B » moins « b »,
divisé par 2, multiplié par « h »,
divisé par 2 [crochet fermant] plus, [crochet ouvrant]« B » moins « b » divisé par, 2 multiplié par « H », divisé
par 2 [crochet fermant]. Élève 2 : Un trapèze dont la base est nommée « B » majuscule, est divisé en 2 partie,
soit un triangle équilatéral
et un parallélogramme. La hauteur du triangle est « H » et la base du parallélogramme est « b ». « A » égal, « b »
multiplié par, « H » plus [crochet ouvrant] (parenthèse ouvrante) « B » moins « b » (parenthèse
fermante) multiplié par « h », divisé par 2 [crochet fermant].Élève 3 : Un trapèze dont la base est nommée « B »
majuscule, est divisé en 2 parties. Soit 2 triangles scalènes.
La hauteur du premier triangle est « h », et la base du deuxième triangle est « b ». « A » égal, « b » multiplié
par « h », divisé par 2 plus « B » multiplié par « H », divisé par 2.
Au moment de l’échange mathématique, comparer les équations qu’ont écrites les élèves, puis déterminer une formule pour calculer l’aire d’un trapèze. Animer une discussion en groupe-classe au sujet de l’efficacité des solutions présentées.
Vérifier avec les élèves la formule obtenue en calculant l’aire d’autres trapèzes orientés de diverses façons (base plus longue au haut, angle droit, angle non symétrique, etc.)
Habiletés à développer relatives à la visualisation spatiale :
- Perception des relations spatiales
- Rotation mentale
Source : Guide d’enseignement efficace des mathématiques, de la 7e à la 10e année, p. 15-17.