E1.3 Situer et lire des coordonnées dans les quatre quadrants d’un plan cartésien, et décrire les déplacements d’une coordonnée à l’autre à l’aide de translations.
HABILETÉ : SITUER DES COORDONNÉES DANS LES QUATRE QUADRANTS D’UN PLAN CARTÉSIEN
Pour situer un point ou une coordonnée dans un des quatre quadrants d’un plan cartésien, par exemple A (-3, -4), il faut se déplacer de trois unités vers la gauche à partir de l’origine, puis de quatre unités vers le bas à partir de l’origine.
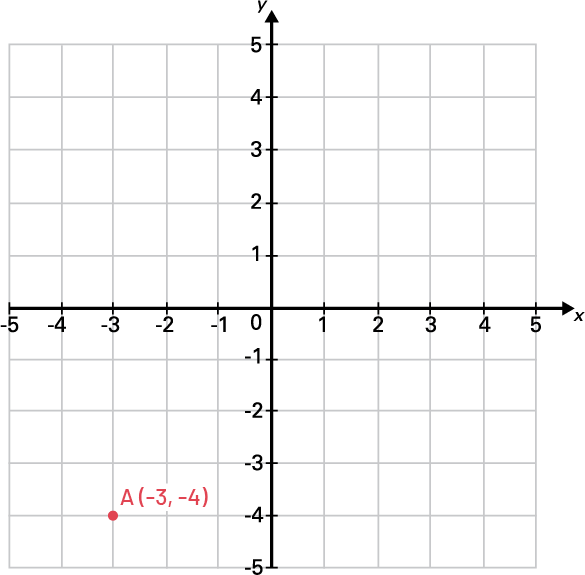
Il faut souligner aux élèves l’importance de l’ordre dans lequel sont placés les nombres dans les coordonnées cartésiennes. Le premier nombre, appelé abscisse, indique la position horizontale du point par rapport à l’origine et est situé en premier. Le second, appelé ordonnée, indique sa position verticale, et est situé en deuxième.
En poursuivant l’utilisation du plan cartésien, les élèves peuvent éprouver une autre difficulté conceptuelle. Cette dernière est liée à l’utilisation de l’échelle sur les axes gradués. La difficulté surgit lorsque les élèves doivent situer sur le plan un point dont les coordonnées ne correspondent pas à une droite verticale ou horizontale ou à un nombre sur les axes. Par exemple, dans un plan où les axes sont gradués selon une échelle 1 : 2, on situe les nombres pairs le long des axes. Cependant, les droites correspondant aux nombres impairs ne sont pas tracées. Les élèves peuvent alors croire qu’un point tel que (7, 5), dont les coordonnées sont impaires, ne peut être situé sur le plan puisqu’elles et ils n’y voient pas de nombres impairs ou de droites qui les représentent. Les élèves doivent comprendre qu’il est possible de situer ce point en se représentant mentalement des droites horizontales et verticales entre les droites déjà tracées.
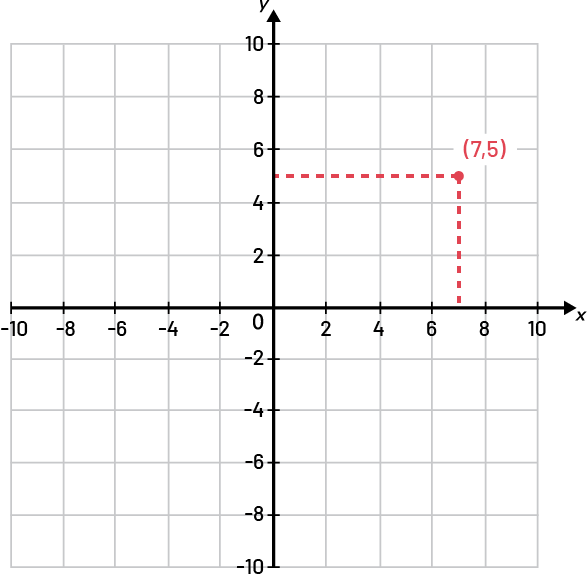
Source : adapté de Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 25-26.
HABILETÉ : LIRE UNE COORDONNÉE DANS LES QUATRE QUADRANTS D’UN PLAN CARTÉSIEN
Pour lire une coordonnée dans les quatre quadrants d’un plan cartésien, il faut indiquer les nombres sur les axes vertical et horizontal. Il faut lire le nombre qui correspond à la position horizontale du point par rapport à l’origine en premier et le nombre qui correspond à la position verticale du point par rapport à l’origine par la suite. Une position horizontale d’un point à la droite du point d’origine est un nombre positif. Une position horizontale d’un point à la gauche du point d’origine est un nombre négatif. Une position verticale d’un point au-dessus du point d’origine est un nombre positif. Une position verticale d’un point sous le point d’origine est un nombre négatif. Les élèves doivent comprendre que les coordonnées cartésiennes définissent un des points d’intersection des droites et non une des cases formées par celles-ci.
Source : adapté de Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 25.
HABILETÉ : DÉCRIRE LES DÉPLACEMENTS D’UNE COORDONNÉE À L’AUTRE À L’AIDE DE TRANSLATIONS
Pour décrire une translation oblique, il faut vérifier à la fois le déplacement horizontal et le déplacement vertical. Pour ce faire, les élèves utilisent une notation symbolique entre parenthèses. Par exemple, une translation de trois unités vers la droite et de deux unités vers le bas est représentée symboliquement par (3D, 2B) ou (3→, 2↓) ou (3, -2). Il est préférable d’habituer les élèves à toujours décrire la translation en indiquant d’abord le déplacement horizontal et ensuite le déplacement vertical.
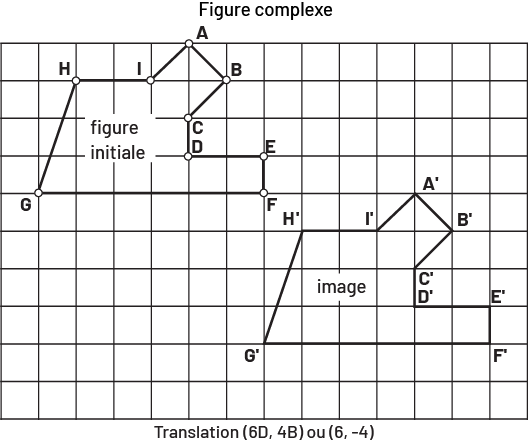Image Il y a une grille dans laquelle se trouve deux figures identiques. La première, est la figure
initiale, elle a les points « a », « b », « c », « d », « e », « f », « g » et « h ». La deuxième figure, a les points
« a » prime, « b » prime, « c » prime, « d » prime, « e » prime, « f » prime, « g » prime et « h » prime. Au- dessus
de la grille est écrit: figure complexe. En-dessous est écrit: translation (parenthèse ouvrante) six « d », quatre « b
» (parenthèse fermante) ou (parenthèse ouvrante) six, moins quatre (parenthèse fermante).
À partir du cycle moyen, les élèves déterminent des translations horizontales, verticales ou obliques définies à l’aide d’une flèche. Cette flèche peut être placée sur la figure ou à l’extérieur de la figure. La direction de la flèche correspond à la direction de la translation et sa longueur correspond à la grandeur du déplacement.
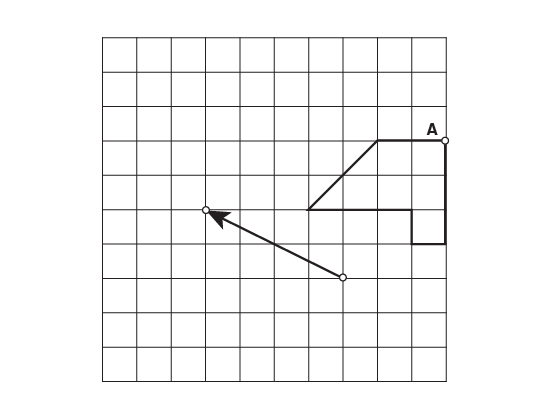
Pour déterminer la translation, les élèves doivent déterminer la grandeur des déplacements horizontal et vertical représentés par la flèche. Par exemple, la flèche dans la figure suivante définit la translation (4G, 2H) ou (-4, 2), soit un déplacement de quatre unités vers la gauche et de deux unités vers le haut.
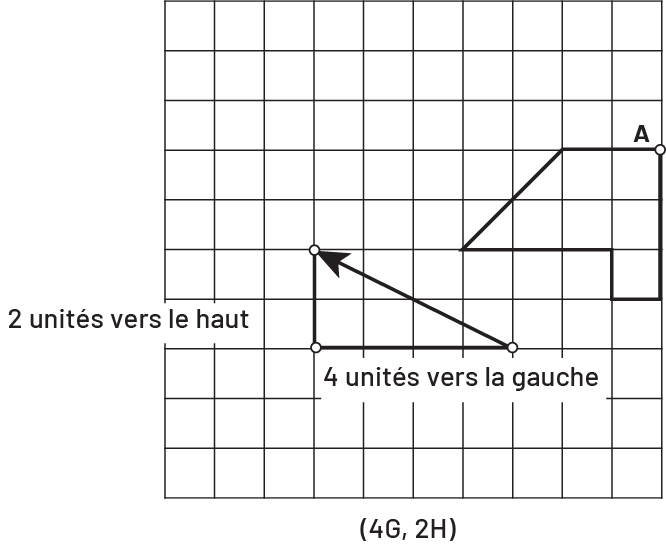Image Une grille dans laquelle se trouve une figure marquée par un point « a ». À la diagonale de la
figure, il y a une flèche oblique vers le haut à la gauche. La flèche forme un côté d’un triangle rectangle. Sur le
côté de ce triangle est écrit: deux unités vers le haut; sous le triangle est écrit: quatre unités vers la gauche.
Sous la grille est écrit: (parenthèse ouvrante) quatre « g », deux « h » (parenthèse fermante).
Au moment d’une translation, tous les points de la figure initiale subissent le même déplacement, c’est-à-dire que tous les points de la figure initiale sont déplacés dans la même direction et sont équidistants des points correspondants de l’image
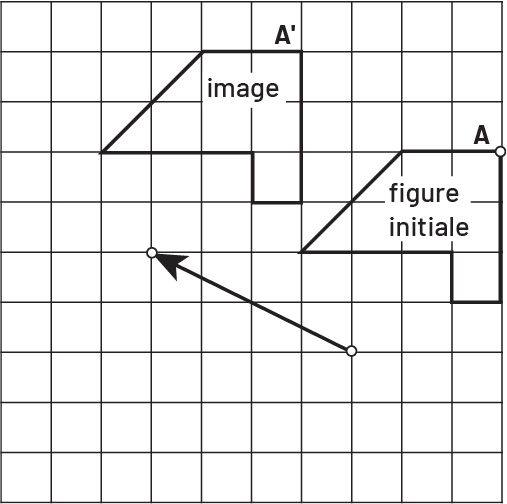Image Une grille dans laquelle se trouve deux figures. La première,
soit la figure initiale, est marquée par un point « a ». La seconde, soit l’image, est marquée par un point « a »
prime. Sous les figures, il y a une flèche oblique vers le haut à la gauche.
Chaque point de la figure initiale a subi une translation de 4 unités vers la gauche et de 2 unités vers le haut.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 28-30.
CONNAISSANCE : PLAN CARTÉSIEN
Le plan cartésien est un système de repérage cartésien pour situer avec précision la position d’un point dans un plan.
En 6e année, les élèves utilisent un système de repérage cartésien pour situer avec plus de précision la position d’un point dans un plan. Deux axes perpendiculaires ser-vent à définir ce plan : l’un horizontal identifié par x et appelé l’axe des x, l’autre vertical identifié par y et appelé l’axe des y. Le point de rencontre de ces axes, appelé l’origine, sert de point de repère. Les axes divisent le plan en quatre régions appelées quadrants.
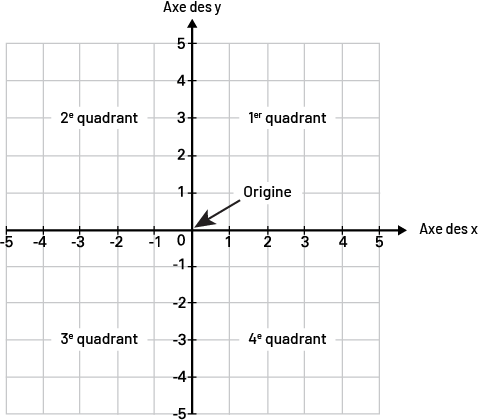Image Un plan cartésien identifiant les quatre quadrants, partant du premier du côté supérieur à la
droite et allant du sens contraire des aiguilles d’une montre. Les cinq colonnes à l’axe des « x » et cinq rangées à
l'axe des « y » sont numérotés. Le point d’origine est démarqué par une flèche.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 24.
CONNAISSANCE : UNE COORDONNÉE
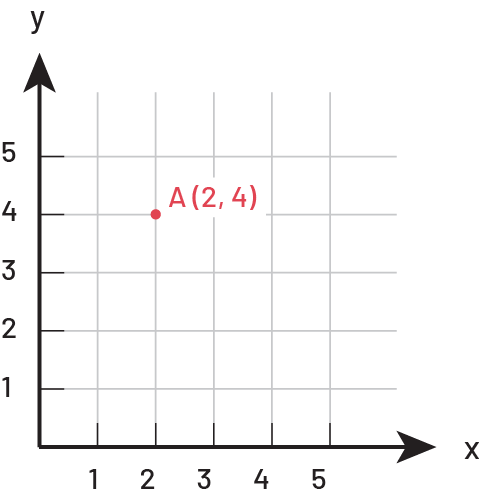
Le système de coordonnées cartésiennes permet de situer un point dans ce plan. Les coordonnées sont écrites entre parenthèses et sont séparées par une virgule comme suit : le point A (2, 4). Par convention, le premier nombre, appelé abscisse, indique la position horizontale du point par rapport à l’origine, et le deuxième, appelé ordonnée, indique sa position verticale.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 25.
CONNAISSANCE : TRANSLATION
La translation est définie par sa grandeur et sa direction (représentées symboliquement par des coordonnées ou par une flèche). Elle représente un déplacement linéaire, horizontal, vertical ou oblique dans lequel la figure initiale et l’image sont congruentes. La distance entre chaque point sur la figure initiale et le point correspondant sur l’image est constante. L’orientation de l’image est la même que l’orientation de la figure initiale.
Image Il y a deux figures identiques sur une grille. Le point « a » sur la première figure est lié au
point « a » prime sur la deuxième. Une autre ligne parallèle lie la base de la figure. À la diagonale, il y a une
flèche oblique vers le bas, à la droite. Sous la grille est écrit: translation (parenthèse ouvrante) quatre « d »,
quatre « b » (parenthèse fermante) ou (parenthèse ouvrante) quatre, moins quatre (parenthèse fermante)
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 36-37.