E2.3 Utiliser les propriétés des angles supplémentaires, complémentaires, opposés ainsi que des angles intérieurs et extérieurs pour déterminer les mesures d’angles manquantes.
HABILETÉ : UTILISER LES PROPRIÉTÉS DES ANGLES POUR DÉTERMINER LES MESURES D’ANGLES MANQUANTES
Les propriétés des angles peuvent servir à trouver des mesures d’angle inconnues.
- Un angle plat mesure 180°; en sachant cela, il est possible de déterminer la mesure d’un angle supplémentaire ainsi que de l’angle extérieur d’un polygone.
- Un angle droit mesure 90°; en sachant cela, il est possible de déterminer la mesure d’un angle complémentaire.
- La somme des angles intérieurs d’un quadrilatère est de 360°; en sachant cela, il est possible de déterminer une mesure d’angle manquante dans un quadrilatère.
- La somme des angles intérieurs d’un triangle est de 180°; en sachant cela, il est possible de déterminer une mesure d’angle manquante dans un triangle.
Ces propriétés peuvent servir à trouver d’autres mesures inconnues (par exemple, celle de l’angle extérieur d’un polygone) ou à expliquer la raison pour laquelle des angles opposés sont égaux.
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
Par exemple, on observe les angles de ce triangle.
- ∠A, ∠B et ∠C sont à l’intérieur du triangle △ABC
- ∠A = 110°
- ∠B = 50°
- ∠C = ?°
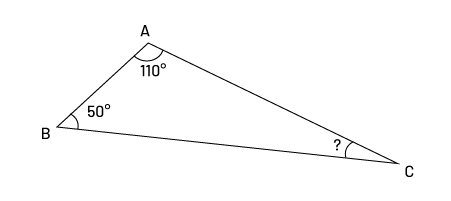
L’élève qui a découvert et généralisé que la somme des angles intérieurs de tous les triangles est égale à 180 degrés peut trouver la valeur de l’angle inconnu en soustrayant la somme des deux angles connus à 180.
Consulter ce document afin de vous familiariser avec la somme des angles intérieurs des polygones. À noter qu’il importe de faire découvrir et de généraliser ces sommes en explorant des activités.
CONNAISSANCE : MESURE DE L’ANGLE
Il est important que l’élève comprenne que la mesure de l’angle fait état de l’amplitude d’une « ouverture ».
L’angle peut être déterminé par :
- deux segments de droite;
- deux demi-droites de même origine;
- deux demi-plans qui se croisent.
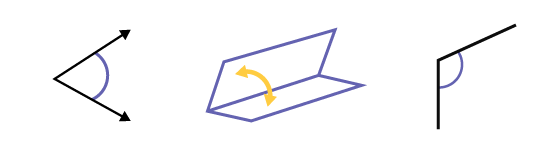 Image Il y a trois illustrations. La première est d’un angle aigu
formé par deux flèches. La deuxième est d’un angle ouvert, indiquée par une flèche. La troisième est d’un angle obtus
formé par deux segments de droite.
Image Il y a trois illustrations. La première est d’un angle aigu
formé par deux flèches. La deuxième est d’un angle ouvert, indiquée par une flèche. La troisième est d’un angle obtus
formé par deux segments de droite.
Au cours de l’exploration des angles, les erreurs courantes des élèves sont liées à leurs représentations fautives et à leur visualisation. En effet, certaines et certains élèves associent l’amplitude de l’angle à la longueur des demi-droites qui le forment, puisque l’ouverture entre les demi-droites s’élargit.
Par exemple, je pense que l’angle A illustré ci-dessous est plus petit que l’angle B, car les lignes qui forment l’angle A sont plus courtes.

Lorsqu’on propose aux élèves des contextes signifiants pour s’exercer à mesurer et à comparer des angles qui sont représentés de diverses façons, elles et ils développent une compréhension approfondie du concept de l’angle et de la mesure de celui-ci. Dans l’exemple ci-dessous, les angles sont équivalents. Toutefois, les segments qui les composent sont de longueurs différentes.
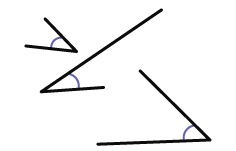
Lorsque les élèves sont capables de comparer l’amplitude des angles sans tenir compte de la longueur des demi-droites qui forment ces angles, elles et ils sont prêts à commencer à mesurer des angles avec précision.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 15-19.
CONNAISSANCE : PROPRIÉTÉS DES ANGLES
Propriétés des angles
ANGLES ADJACENTSDeux angles sont adjacents s'ils ont le même sommet et un côté commun et s'ils sont situés de part et d'autre du côté commun. Par exemple, ∠zoy est adjacent à ∠yox. |
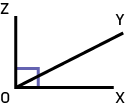 |
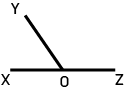
ANGLES SUPPLÉMENTAIRESDeux angles sont supplémentaires lorsque la somme de leur mesure est à égale à 180o. Par exemple, ∠xoy et ∠yoz sont supplémentaires et adjacents. |
 |
ANGLES COMPLÉMENTAIRESDeux angles sont complémentaires lorsque la somme de leur mesure est 90o. Par exemple, ∠yoz et ∠xoy sont complémentaires et adjacents. |
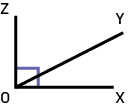 |
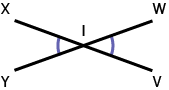
ANGLES OPPOSÉS PAR LE SOMMETDeux angles formés par l'intersection de deux droites ou de quatre segments de droites orientés dans la même direction deux à deux. Ils sont toujours congrus. Par exemple, ∠xly es opposé à ∠wlv. |
 |
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 16.
Vidéos explicatifs de l’utilisation des propriétés des angles supplémentaires et complémentaires :
Source : L'@telier - Ressources pédagogiques en ligne (atelier.on.ca).
CONNAISSANCE : ANGLES INTÉRIEURS ET EXTÉRIEURS
Angles intérieurs
Les élèves doivent être en mesure de reconnaître les angles formés à l’intérieur d’une figure plane à chacun de ses sommets.
Dans les exemples ci-dessous, on voit que le triangle est formé de trois angles intérieurs et le quadrilatère, de quatre angles intérieurs.
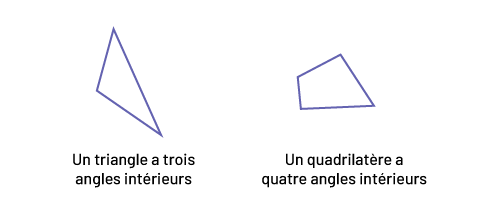 Image Il y a deux figures : soit un triangle et un quadrilatère. Sous la
première est écrit: un triangle a trois angles intérieurs. Sous la deuxième est écrit: un quadrilatère a quatre angles
intérieurs.
Image Il y a deux figures : soit un triangle et un quadrilatère. Sous la
première est écrit: un triangle a trois angles intérieurs. Sous la deuxième est écrit: un quadrilatère a quatre angles
intérieurs.
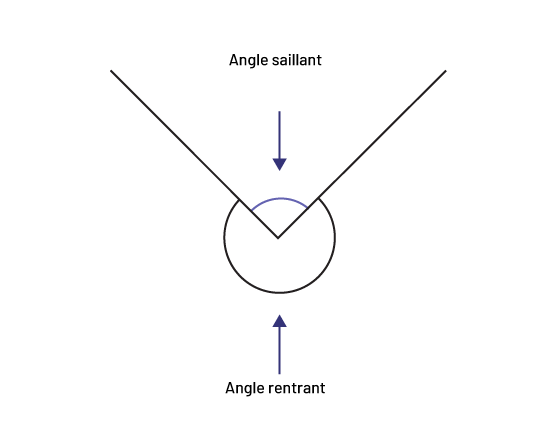
Lorsque deux segments de droite sont tracés à partir d’un point commun, ils forment en réalité deux angles différents (figure ci-dessous), soit l’angle saillant (angle dont la mesure se situe entre 0° et 180°) et l’angle rentrant (angle dont la mesure se situe entre 180° et 360°).
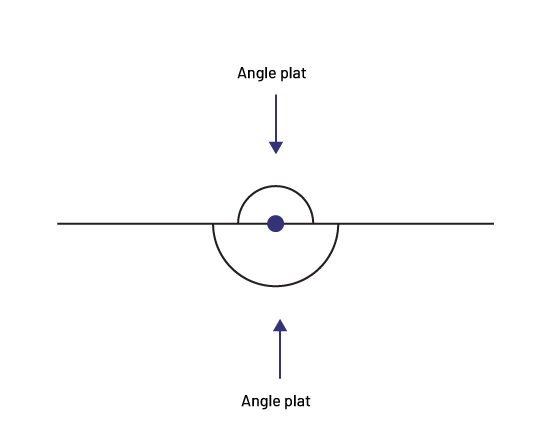
Il existe un cas d’exception où les deux segments de droite ne forment pas deux angles différents (figure ci-dessous). C’est le cas lorsque les deux segments de droite sont alignés, puisqu’ils forment alors deux angles égaux de 180° (angles plats).
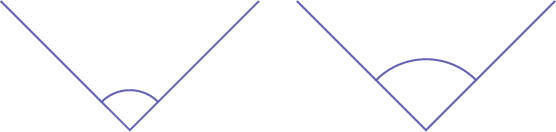
Par convention, on trace un arc entre les deux segments de droite pour indiquer l’angle dont il est question. Il importe que les élèves n’associent pas la grandeur de l’arc à la mesure de l’angle. Par exemple, les deux angles représentés ci-dessous sont congrus même si les arcs peuvent donner l’impression qu’un angle est plus grand que l’autre.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 23-24.
Angles extérieurs
L’angle extérieur est formé d’un des côtés d’un polygone et du prolongement de l’un de ses côtés adjacents.
Dans un polygone, l’angle extérieur et l’angle intérieur adjacent sont supplémentaires, c’est-à-dire que leur somme est toujours 180°.
La somme des angles extérieurs d’un polygone est toujours 360°.
Exemples de polygones
Hexagone
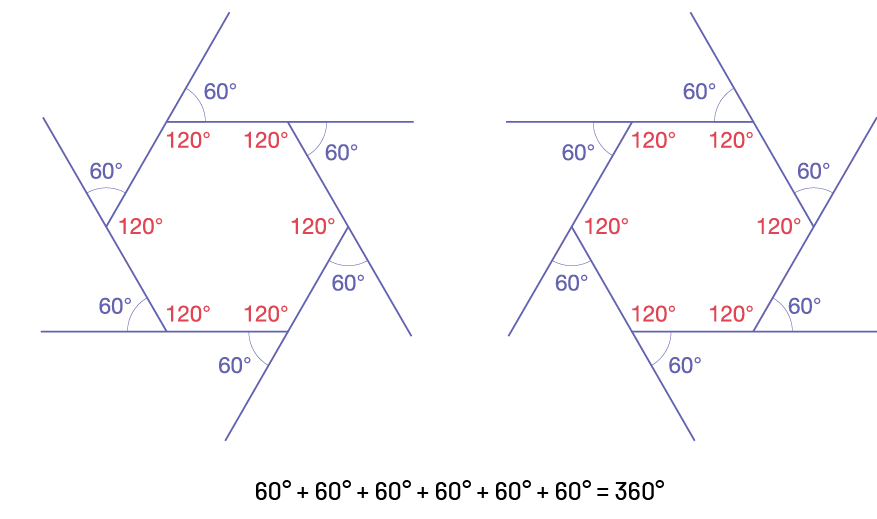 Image Il y a deux hexagones dont les angles sont mesurés dans
le sens contraire des aiguilles d’une montre dans la première figure, et dans le sens des aiguilles d’une montre dans
la seconde. Sous les hexagones est écrit: 60 degrés plus 60 degrés plus 60 degrés plus 60 degrés plus 60 degrés plus
60 degrés égale à 360 degrés.
Image Il y a deux hexagones dont les angles sont mesurés dans
le sens contraire des aiguilles d’une montre dans la première figure, et dans le sens des aiguilles d’une montre dans
la seconde. Sous les hexagones est écrit: 60 degrés plus 60 degrés plus 60 degrés plus 60 degrés plus 60 degrés plus
60 degrés égale à 360 degrés.
Rectangle
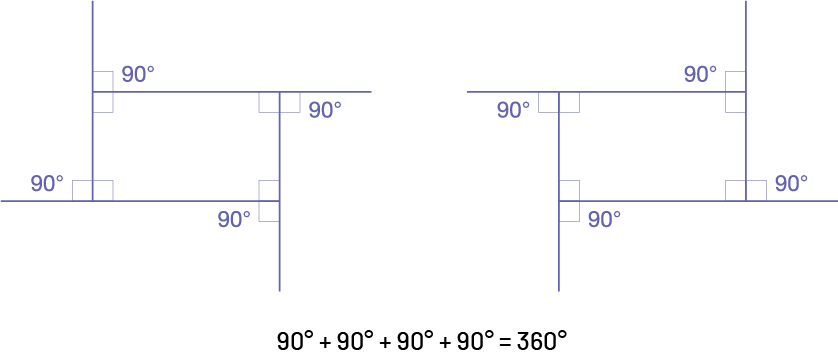 Image Il y a deux rectangles identiques donc les angles sont
mesurés dans le sens contraire des aiguilles d’une montre dans la première figure, et dans le sens des aiguilles d’une
montre dans la seconde. Sous les figures est écrit: 90 degrés plus 90 degrés plus 90 degrés plus 90 degrés égale à 360
degrés.
Image Il y a deux rectangles identiques donc les angles sont
mesurés dans le sens contraire des aiguilles d’une montre dans la première figure, et dans le sens des aiguilles d’une
montre dans la seconde. Sous les figures est écrit: 90 degrés plus 90 degrés plus 90 degrés plus 90 degrés égale à 360
degrés.
Source : L'@telier - Ressources pédagogiques en ligne (atelier.on.ca).
Consulter ce lien du site Web l’@telier qui propose des animations portant sur la propriété des angles intérieurs et la propriété des angles extérieurs d’un triangle.
