E2.4 Déterminer l’aire de trapèzes, de losanges, de cerfs-volants ainsi que de polygones complexes en les décomposant en figures planes avec des aires connues.
HABILETÉ : DÉTERMINER L’AIRE DE TRAPÈZES, DE LOSANGES, DE CERFS-VOLANTS ET DES POLYGONES COMPLEXES EN LES DÉCOMPOSANT EN FIGURES PLANES AVEC DES AIRES CONNUES
En mesure, l’additivité désigne le concept selon lequel la mesure d’un attribut d’un objet est égale à la somme des mesures de ses parties.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 52.
L’élève qui comprend le concept fondamental de l’additivité réalise que l’aire d’un polygone est égale à la somme de l’aire de chacune de ses parties.
Par exemple, si on demande à l’élève de déterminer l’aire du polygone ci-dessous, il suffit de le décomposer en un rectangle et en un triangle afin de déterminer l’aire de chacun et d’en faire la somme.
Les élèves peuvent donc utiliser leurs connaissances de l’aire d’un triangle, d’un carré et d’un rectangle afin de décomposer les quadrilatères (trapèze, losange et cerf-volant) ainsi que des polygones complexes afin de déterminer la somme de l’aire de ses parties.
De plus, l’élève qui comprend le concept de conservation réalise que l’aire d’une surface demeure la même, que la surface soit déplacée, transformée ou décomposée.
Source : Fiche de la 4e à la 6e année_Attribut aire, p. 3.
Exemple du concept de conservation de l’aire
L’aire des figures 1 et 2 ci-dessous est la même que l’aire du carré, car les trois figures sont construites à partir des sept mêmes pièces d’un jeu de tangram.
Le personnel enseignant doit profiter de diverses situations pour inciter les élèves à reconnaître qu’il y a un lien étroit entre le concept d’additivité et le concept de conservation.
Par exemple, lorsque les élèves construisent différentes figures à partir des sept pièces d’un jeu de tangram, il les incite à reconnaître que l’aire globale de toutes les figures est la même (concept de conservation) et qu’elle est égale à la somme des aires de chacune des sept pièces qui la composent (concept d’additivité).
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 50, 53-54.
Les élèves déterminent l’aire de trapèzes en les décomposant en figures planes ayant des aires connues.
Il existe différentes façons de décomposer et de composer des trapèzes pour former des rectangles, des parallélogrammes ou des triangles. Les différentes stratégies de composition ont leurs formules propres, mais équivalentes.
- Un trapèze peut être décomposé en deux triangles et en un rectangle dont les aires sont ensuite combinées.
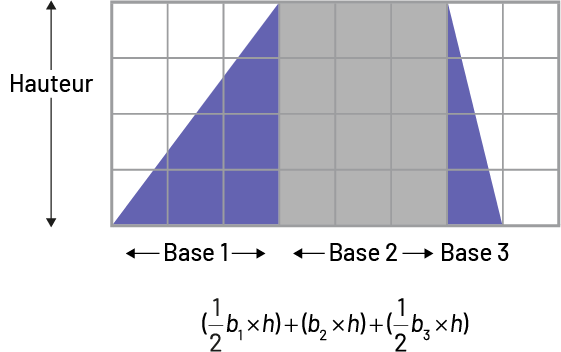Image Il y a une grille de huit colonnes et quatre rangées. Dans la grille il y a un trapèze qui est
divisé en 2
triangles et un parallélogramme. La hauteur, des figures est indiquée par une flèche. La base du premier triangle
est indiquée par une flèche, base un. La base du parallélogramme est la base 2 et la base du deuxième triangle, base
3. Sous la grille il y a une équation: (parenthèse ouvrante) une demie « b » indice un, multiplié par « h »
(parenthèse fermante), plus, (parenthèse
ouvrante) « b » indice 2, multiplié par « h » (parenthèse fermante), plus (parenthèse ouvrante) une demie « b »
indice 3, multiplié par « h » (parenthèse fermante).
- Un trapèze peut être doublé pour créer un parallélogramme dont l’aire est ensuite divisée en deux.
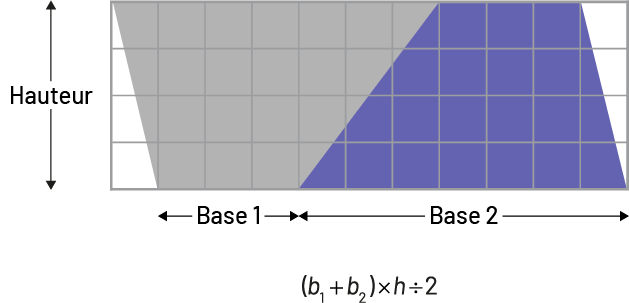Image Il y a une grille de onze colonnes et quatre rangées. Dans la grille il y a un trapèze qui
est
doublé pour
former un parallélogramme. Ce parallélogramme est divisé par sa hauteur, sa base un et sa base deux. Sous la grille
il y a une équation: (Parenthèse ouvrante) « b » indice un, plus « b » indice 2 (parenthèse fermante), multiplié par «
h » divisé par 2.
- Deux triangles peuvent être ajoutés à un trapèze pour créer un grand rectangle duquel leur aire est ensuite soustraite.
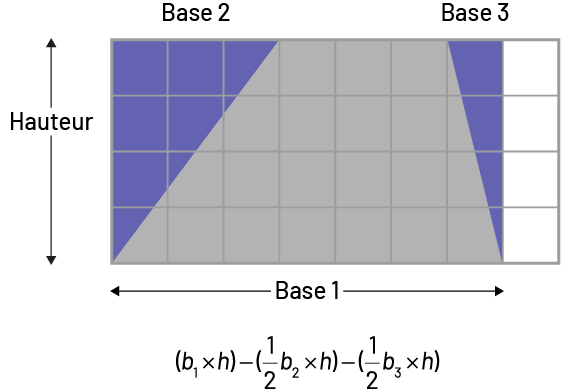Image Il y a une grille de huit colonnes et quatre rangées. Dans la grille il y a un trapèze et
deux
triangles qui
forme un rectangle. Ce quadrilatère est divisé par sa hauteur, sa base un, sa base deux, et sa base trois. Sous la
grille il y a une équation: (parenthèse ouvrante) « b » indice un, multiplié par « h » (parenthèse fermante), moins,
(parenthèse ouvrante) une
demie « b » indice 2, multiplié par « h » (parenthèse fermante), moins (parenthèse ouvrante) une demie « b » indice
3, multiplié par « h » (parenthèse fermante).
- Un trapèze peut être composé pour former un rectangle ayant la même aire et dont la base équivaut à la moyenne des deux bases du trapèze (par exemple, grâce à deux triangles formés à partir du milieu des côtés).
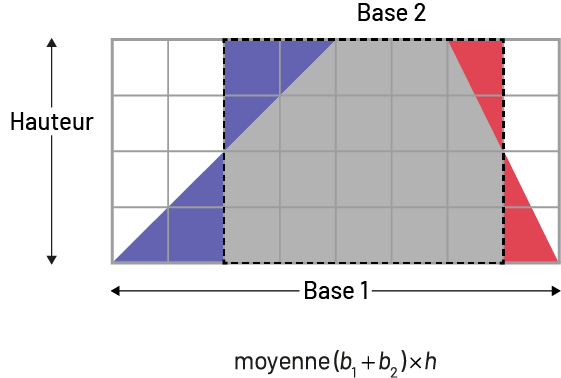Image Il y a une grille de huit colonnes et quatre rangées. Dans la grille il y a une figure
constituée d’un
trapèze et quatre triangles. Ce parallélogramme est divisé par sa hauteur, sa base un, sa base deux, et sa base
trois. Sous la grille il y a une équation : moyenne (parenthèse ouvrante) « b » indice un, plus « b » indice 2
(parenthèse fermante) multiplié par « h ».
Les stratégies de composition et de décomposition servant à trouver l’aire d’un trapèze permettent aussi de déterminer l’aire d’un cerf-volant (décomposé en deux triangles) et de polygones complexes.
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
CONNAISSANCE : POLYGONE COMPLEXE
Un polygone complexe a une aire composée de plusieurs polygones.
