SITUATION D’APPRENTISSAGE 1 : TOUT UN CASSE-TÊTE!
Durée totale : 140 minutes
Sommaire
Dans cette situation d’apprentissage, les élèves construisent un casse-tête formé d’un ensemble de quadrilatères conformément à une série de critères donnés.
|
Attente |
Contenus d’apprentissage |
|
E1. Raisonnement géométrique et spatial Décrire et représenter la forme, la position et le déplacement en se servant de propriétés géométriques et de relations spatiales pour s’orienter dans le monde qui l’entoure. |
E1.1 Créer des listes des propriétés géométriques de divers types de quadrilatères, y compris les propriétés des diagonales, la symétrie rotationnelle et les axes de symétrie. E1.4 Décrire et effectuer des combinaisons de translations, de réflexions et de rotations jusqu’à 360° dans une grille, et prédire les résultats de ces transformations. |
Intention pédagogique
Cette situation d’apprentissage a pour but d’amener les élèves :
- à tenir compte des propriétés de différents quadrilatères;
- à visualiser un dallage formé de quadrilatères;
- à utiliser un logiciel ou une application de géométrie dynamique;
- à utiliser des stratégies de résolution de problèmes.
|
Contexte pédagogique |
Préalables |
|
Au cours des années d’études précédentes, les élèves ont appris à identifier et à construire diverses figures planes, et à les classer selon des propriétés données. En 6e année, elles et ils accordent une attention particulière aux propriétés communes et aux propriétés distinctes des quadrilatères. |
La présente situation d’apprentissage permet aux élèves de consolider leur compréhension des propriétés des quadrilatères, de travailler sur le plan de l’analyse et de cheminer vers la déduction informelle de la pensée géométrique selon le modèle des chercheurs van Hiele (voir Fondements généraux). Elle leur permet aussi d’apprendre à utiliser un logiciel de géométrie dynamique. Pour être en mesure de réaliser cette situation d’apprentissage, les élèves doivent :
|
Vocabulaire mathématique
symétrique, congruent, rectangle, quadrilatère, deltoïde, trapèze, cerf-volant, losange, angle droit, angle aigu, angle obtus
Matériel
- tableau blanc interactif
- annexe Tout un casse-tête! (une copie par élève)
- logiciel ou application de géométrie dynamique
- rapporteurs d’angles et règles
- ordinateurs (un par élève)
- papier
- crayons
Activité préparatoire facultative
Durée : environ 20 minutes
Expliquer aux élèves la façon de construire des segments de droite et des polygones en utilisant un logiciel ou une application de géométrie dynamique et leur demander d’en construire quelques-uns. Ensuite, leur demander de construire un triangle isocèle et un triangle équilatéral, puis de vérifier la congruence des côtés.
Avant l’apprentissage (mise en train)
Durée : environs 10 minutes
Au tableau blanc interactif, afficher l’annexe Tout un casse-tête! et présenter le problème ci-dessous aux élèves.
C’est bien connu, les élèves de 6e année aiment relever de nouveaux défis. À l’aide d’un logiciel ou d’une application de géométrie dynamique, construis un casse-tête en tenant compte des critères ci-dessous. Ton casse-tête doit être :
- symétrique;
- de forme rectangulaire;
- composé seulement de quadrilatères.
Parmi les quadrilatères, tu dois avoir :
- au plus deux paires différentes de quadrilatères congruents ayant chacun quatre angles droits;
- au moins une paire de deltoïdes congruents;
- au moins une paire de trapèzes congruents ayant chacun exactement deux angles droits;
- au moins un cerf-volant ayant exactement un angle droit;
- seulement un losange, celui-ci ayant deux angles obtus de plus de 105°.
Démontre, par écrit, que tu as répondu à tous les critères.
S’assurer que les élèves ont bien compris le défi à relever en posant des questions telles que :
- Qui peut expliquer le défi dans ses mots?
- De quels critères devrez-vous tenir compte au moment de la construction des quadrilatères?
- Quelles sont les propriétés du trapèze? du deltoïde? du cerf-volant? du losange?
- Que signifie le mot congruent?
Pendant l’apprentissage (exploration)
Durée : environ 50 minutes
Remettre une copie de l’annexe Tout un casse-tête! à chaque élève. Préciser que la construction du casse-tête est un travail individuel. Allouer suffisamment de temps pour leur permettre de résoudre le problème.
Observer les élèves et les appuyer dans leur travail sans toutefois leur indiquer la façon de relever le défi. Il faut les amener, par des interventions stratégiques, à réfléchir aux propriétés des quadrilatères qu’elles et ils doivent construire et à en tenir compte dans le choix des stratégies utilisées pour résoudre le problème (par exemple, puisqu’il n’y a qu’un seul losange et que le casse-tête doit être symétrique, le losange doit être placé de part et d’autre de l’axe de symétrie).
|
Observations possibles |
Interventions possibles |
|
Quelques élèves se demandent s’il existe une commande dans le logiciel ou l’application qui permet de reproduire automatiquement un quadrilatère de l’autre côté de l’axe de symétrie. |
Leur demander de préciser la transformation qu’elles et ils doivent utiliser pour assurer la symétrie (une réflexion). |
|
Des élèves construisent trois rectangles. |
|
|
Des élèves construisent rapidement leur casse-tête, mais ne donnent aucune explication pour démontrer qu’elles et ils ont répondu à tous les critères. |
|
Les observations et les interventions permettent de vérifier, dans le cadre d’une évaluation formative, les stratégies utilisées par les élèves pour créer leur casse-tête et leur compréhension des propriétés des quadrilatères. En outre, elles permettent de choisir de façon stratégique, et en fonction de l’intention pédagogique, les élèves qui présenteront leur casse-tête au moment de l’échange mathématique. Pour construire un casse-tête répondant aux critères donnés, les élèves peuvent utiliser plusieurs stratégies. Elles et ils peuvent par exemple :
- tracer une forme rectangulaire afin de définir le contour du casse-tête;
- déterminer le point milieu de deux côtés opposés du rectangle et tracer un axe de symétrie (horizontal ou vertical) qui relie ces deux points;
- tracer un axe de symétrie diagonal dans le rectangle;
- dessiner un quadrilatère à l’extérieur du rectangle, le copier et le coller de chaque côté de l’axe de symétrie;
- mesurer les angles ou les côtés d’un quadrilatère afin de s’assurer de respecter ses propriétés;
- utiliser la réflexion ou la rotation pour reproduire un quadrilatère dans la seconde moitié du rectangle;
- utiliser une grille pour faciliter la construction et assurer la congruence et la symétrie;
- construire un quadrilatère dans la première moitié du rectangle, puis utiliser des droites horizontales et des mesures pour déterminer l’emplacement du quadrilatère dans l’autre moitié;
- construire un quadrilatère dans chaque moitié du rectangle et se fier à l’œil pour leur congruence.
Une fois le casse-tête terminé, dire aux élèves de l’imprimer afin de l’utiliser pendant l’échange mathématique et de
vous le remettre par la suite (voir l’annexe Exemple de
solution pour un exemple d’un casse-tête qui répond à tous les critères de construction). Afin
que les élèves se préparent pour l’échange mathématique, leur allouer suffisamment de temps pour qu’elles et ils
puissent réfléchir à leurs stratégies, aux étapes suivies, etc.
Après l’apprentissage (objectivation/échange mathématique)
Durée : environ 30 minutes
Demander aux élèves choisis de communiquer leur solution, leur démarche et leurs observations.
Note : Le choix des élèves qui présentent leur casse-tête est très important, puisque c’est au moyen de ces échanges qu’elles et ils pourront comparer leurs stratégies avec celles des autres et objectiver leur apprentissage. On peut aussi choisir une ou un élève qui a utilisé une stratégie qui n’a pas donné les résultats escomptés. En effet, les non-exemples sont aussi profitables dans l’apprentissage des mathématiques dans la mesure où l’on discute des raisons qui font que la stratégie s’est avérée inefficace dans cette situation particulière.
Après chaque présentation, les autres élèves enrichissent l’échange mathématique en posant des questions et en faisant des observations pertinentes dans un climat de respect propre à une communauté d’apprentissage. L’enseignante ou l’enseignant pose au besoin des questions telles que :
- Qui peut expliquer dans ses mots la stratégie qu’on vient de présenter?
- Est-ce une stratégie efficace?
- Est-ce que d’autres élèves ont utilisé cette stratégie?
- Est-ce que quelqu’un est arrivé au même résultat d’une autre façon?
- Est-ce que tous les critères de construction ont été respectés?
- Est-ce que les arguments présentés sont clairs, justes et convaincants?
Encourager l’emploi d’un vocabulaire précis et de termes de causalité dans la communication. Voici quelques exemples d’observations possibles :
- Je savais que je devais placer le losange sur l’axe de symétrie parce qu’il n’y en a qu’un et que le casse-tête doit être symétrique.
- Ce quadrilatère est un losange (en le montrant du doigt sur sa copie imprimée), car les mesures données ici confirment qu’il a quatre côtés congrus.
Différenciation pédagogique
|
Pour faciliter la tâche |
Pour enrichir la tâche |
|
|
Suivi à la maison
À la maison les élèves peuvent, à l’aide d’un rapporteur et d’une règle ou d’un logiciel ou d’une application de géométrie dynamique, construire un casse-tête rectangulaire symétrique avec seulement une sorte de polygone (par exemple, seulement des rectangles, seulement des triangles).
Activité : un nouveau défi!
Proposer, aux élèves, le défi suivant : « En utilisant seulement quatre couleurs, coloriez tous les quadrilatères de votre casse-tête sans que deux quadrilatères unis par un segment de droite commun aient la même couleur. Toutefois, si deux quadrilatères ont seulement un point en commun, ils peuvent être de la même couleur. »
Note : Il est possible que des élèves puissent colorier leur casse-tête en utilisant moins de quatre couleurs, surtout si le casse-tête est relativement simple. Par contre, même pour les casse-têtes les plus complexes, il est toujours possible de les colorier en utilisant au plus quatre couleurs. Ce défi est analogue à un problème que les mathématiciennes et les mathématiciens ont mis plus de cent ans à résoudre. Il s’agissait de prouver qu’il est toujours possible de colorier tous les pays sur une carte du monde avec seulement quatre couleurs différentes, sans que deux pays ayant une ligne frontalière commune soient de la même couleur. Il est possible de trouver plus d’information dans Internet au sujet de ce célèbre problème en entrant « Théorème des quatre couleurs » dans un moteur de recherche.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 69-77.
SITUATION D’APPRENTISSAGE 2 : LA BOÎTE À PENTACUBES
Durée totale : environ 90 minutes
Sommaire
Dans cette situation d’apprentissage, les élèves créent un jeu qui consiste à insérer des solides (des pentacubes plats) dans des ouvertures découpées dans une boîte à souliers.
|
Attente |
Contenus d’apprentissage |
|
E1.Raisonnement géométrique et spatial Décrire et représenter la forme, la position et la déplacement en se servant de propriétés géométriques et de relations spatiales pour s’orienter dans le monde qui l’entoure. |
E1.1 Créer des listes des propriétés géométriques de divers types de quadrilatères, y compris les propriétés des diagonales, la symétrie rotationnelle et les axes de symétrie. E1.4 Décrire et effectuer des combinaisons de translations, de réflexions et de rotations jusqu’à 360° dans une grille, et prédire les résultats de ces transformations. |
Intention pédagogique
Cette situation d’apprentissage a pour but d’amener les élèves :
- à visualiser les objets aussi bien dans un espace bidimensionnel (celui des figures planes) que dans un espace tridimensionnel (celui des solides);
- à visualiser l’image de figures à la suite de rotations, de réflexions et de translations;
- à appliquer des stratégies de résolution de problèmes.
|
Contexte pédagogique |
Préalables |
|
Au cours du cycle primaire, les élèves ont appris à effectuer des translations et des réflexions de figures planes, et ont développé l’habileté à visualiser la position de l’image d’une figure plane obtenue à la suite de l’une ou de l’autre de ces transformations. Au cycle moyen, les élèves poursuivent l’étude des transformations, notamment en effectuant des rotations. |
La présente situation d’apprentissage permet aux élèves, dans un contexte de résolution de problèmes, de consolider leur compréhension des concepts de transformation, de congruence et d’aire. Elle leur permet aussi de parfaire leur habileté à visualiser la position d’un objet à la suite d’une transformation géométrique. Pour être en mesure de réaliser cette situation d’apprentissage, les élèves doivent :
|
Vocabulaire mathématique
pentomino, pentacube, pentacube plat, face, rotation, réflexion, translation, congruence, aire, unités carrées
Matériel
- tableau blanc interactif
- boîtes à souliers (une par équipe)
- ciseaux (une paire par équipe)
- grandes feuilles de papier
- cubes emboîtables de 2 cm × 2 cm (60 par équipe)
- ruban-cache
- annexe La boîte à pentacubes
- annexe Les 12 pentominos (une copie par équipe)
- annexe Les 29 pentacubes
- annexe Notes explicatives
- papier quadrillé
Activité préparatoire facultative
Durée : environ 20 minutes
Cette activité préparatoire facultative permet aux élèves de découvrir les 12 pentominos dans un contexte de résolution de problèmes et de revoir les concepts de congruence et de transformation.
Former des équipes de deux élèves. Leur expliquer ce qu’est un pentomino à l’aide d’un exemple (voir l’annexe Les 12 pentaminos). Remettre à chaque équipe deux feuilles de papier quadrillé de 2 cm × 2 cm (Papier quadrillé) et leur demander de dessiner tous les pentominos qu’elles et ils peuvent trouver. Échanger en groupe-classe et s’assurer que les 12 pentominos sont identifiés. Expliquer aux élèves que chacun des pentominos est associé, en raison de sa forme, à l’une des lettres F, I, L, N, P, T, U, V, W, X, Y et Z.
Avant l’apprentissage (mise en train)
Durée : environ 25 minutes
Écrire le mot pentacube au tableau. Demander aux élèves si elles et ils savent ce qu’est un pentacube (voir l’annexe Notes explicatives). Les inciter à penser à d’autres mots qui ont le même préfixe (par exemple, pentagone, pentomino, pentathlon) et à reconnaître que le préfixe pent- signifie « cinq ». Les élèves devraient alors pouvoir déduire qu’un pentacube est un solide formé de cinq cubes congruents.
Demander à une ou à un élève de construire un pentacube à l’aide de cubes emboîtables et de le montrer à la classe. Préciser que les cubes qui forment un pentacube doivent être reliés les uns aux autres par au moins une face. Leur dire :
- qu’il existe 29 pentacubes différents (voir l’annexe Les 29 pentacubes), parmi lesquels 12 ont deux faces de cinq unités carrées;
- que ces derniers sont généralement appelés les « pentacubes plats » et peuvent, en raison de leur forme, être associés un à un aux 12 pentominos (voir l’annexe Les 12 pentominos) et aux lettres F, I, L, N, P, T, U, V, W, X, Y et Z.
Former des équipes de deux élèves et remettre à chaque équipe 60 cubes emboîtables, du ruban-cache et une copie de l’annexe Les 12 pentominos. Leur demander de se référer aux représentations des pentominos de l’annexe pour construire un ensemble de 12 pentacubes plats et d’identifier chacun, à l’aide d’un morceau de ruban-cache, par la lettre qui lui est associée.
Note : Si les élèves ont fait l’activité préparatoire facultative, elles et ils peuvent utiliser leurs dessins des pentominos au lieu de l’annexe Les 12 pentominos. On peut aussi distribuer aux équipes des ensembles de pentacubes commerciaux au lieu de les faire construire.

Lorsque les équipes sont prêtes, remettre une copie de l’annexe La boîte à pentacubes et présenter le problème dans un contexte intéressant. Par exemple, dire aux élèves :
« L’autre jour, j’ai trouvé un jeu dans le fond d’une armoire. Il s’agit d’une boîte avec différentes ouvertures par lesquelles on doit insérer certains solides. (Leur montrer un tel jeu ou encore leur montrer celui de l’annexe La boîte à pentacubes.) Vous avez peut-être joué avec un jeu comme celui-là lorsque vous étiez très jeunes.
Je me suis dit qu’il serait intéressant de créer un jeu semblable en utilisant des formes géométriques plus complexes, soit les 12 pentacubes plats, et d’offrir aux élèves de 3e année de l’essayer. Vous devez découper cinq ouvertures dans une boîte de carton par lesquelles il sera possible d’insérer chacun des 12 pentacubes plats. Afin que le jeu offre un certain défi à celles et à ceux qui l’essayeront, vous devez respecter les critères suivants. »
Critères
- Chaque jeu doit comprendre seulement cinq ouvertures : une ouverture sur chacun des quatre côtés de la boîte et une sur le dessus, mais aucune dans le fond de la boîte.
- Toutes les ouvertures doivent avoir une aire de 6 unités carrées (une unité carrée correspond à l’aire d’une face d’un cube emboîtable).
- Les 12 pentacubes doivent pouvoir être insérés dans la boîte par l’une des cinq ouvertures à partir d’une des faces dont l’aire mesure 5 unités carrées.
S’assurer que les élèves ont bien compris la tâche à effectuer en posant des questions telles que :
- Quelqu’un peut-il expliquer le problème dans ses mots?
- Quels critères devez-vous respecter au moment de la création du jeu?
- Que veut dire une aire de 6 unités carrées?
- Quelqu’un peut-il nous montrer de quelle façon les pentacubes doivent passer par les ouvertures?
- Comment allez-vous vérifier si votre jeu répond aux critères?
Pendant l’apprentissage (exploration)
Durée : environ 50 minutes
Demander aux équipes de déterminer la forme de chacune des cinq ouvertures avant de commencer à les découper dans les boîtes. Mettre à leur disposition des feuilles de papier quadrillé de 2 cm × 2 cm (annexe Papier quadrillé). Pour résoudre le problème, les élèves peuvent, par essais et erreurs :
- superposer certains pentacubes afin de trouver des arrangements dont l’une des faces a une aire de 6 unités carrées;
- tracer des formes d’ouvertures ayant une aire de 6 unités carrées sur une feuille vierge ou quadrillée et vérifier ensuite les pentacubes qui peuvent passer par chacune.
Allouer suffisamment de temps pour permettre aux élèves d’explorer les possibilités d’ouvertures. Circuler parmi les élèves et intervenir au besoin. Porter une attention particulière aux stratégies utilisées afin de choisir de façon stratégique les équipes qui seront invitées à faire une présentation au cours de l’échange mathématique.
|
Observations possibles |
Interventions possibles |
|
Des élèves conçoivent une ouverture ayant plus de 6 unités carrées. |
Les inviter à vérifier l’aire de chacune de leurs ouvertures et à relire les critères à respecter. |
|
Des élèves ne respectent pas le fait que les pentacubes doivent passer à plat dans l’ouverture. |
Leur demander d’identifier l’une des faces du pentacube dont l’aire mesure 5 unités carrées et de relire les critères à respecter. |
|
Des élèves conçoivent cinq ouvertures, mais il leur reste un pentacube à insérer. |
Les inciter à créer une ouverture qui permettra d’insérer le pentacube qui reste et à redistribuer les autres pentacubes afin d’éliminer une des cinq ouvertures originales. |
|
Des élèves conçoivent leurs ouvertures en considérant seulement une seule des deux faces dont l’aire mesure 5 unités carrées. |
Les inciter à observer attentivement les pentacubes et à analyser les ressemblances et les différences entre les deux faces dont l’aire mesure 5 unités carrées. |
Note 1 : Les deux faces sont congruentes, mais sont l’image l’une de l’autre, comme si elles se reflétaient dans un miroir. Par conséquent, certains pentacubes (pentacubes F, L, N, P, Y et Z) peuvent parfois être insérés dans la boîte par des ouvertures différentes selon la face choisie.
Note 2 : Il existe 35 formes différentes d’ouvertures de 6 unités carrées, soit celles correspondant aux 35 hexominos. Plusieurs combinaisons de cinq de ces ouvertures permettent d’insérer les 12 pentacubes plats. L’exemple ci-dessous présente l’une de ces combinaisons. Dans cet exemple, les pentacubes T, W et Y peuvent être insérés dans la boîte par deux ouvertures différentes.
Exemple
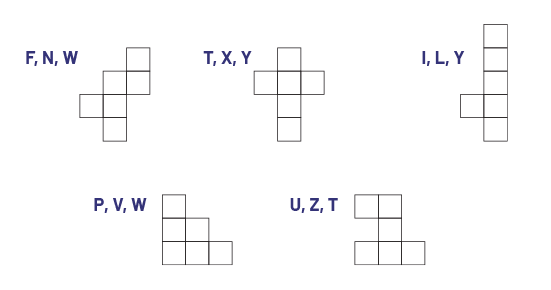 Image Il y a cinq combinaisons de six carrés. À côté de la première
combinaison sont les lettres « f », « n » et « w ». À côté de la deuxième combinaison sont les lettres « t », « x »
et « y ». À côté de la troisième combinaison sont les lettres « i », « l » et « o ». À côté de la quatrième
combinaison sont les lettres « p », « v » et « w ». À côté de la cinquième combinaison sont les lettres « u », « z »
et « t ».
Image Il y a cinq combinaisons de six carrés. À côté de la première
combinaison sont les lettres « f », « n » et « w ». À côté de la deuxième combinaison sont les lettres « t », « x »
et « y ». À côté de la troisième combinaison sont les lettres « i », « l » et « o ». À côté de la quatrième
combinaison sont les lettres « p », « v » et « w ». À côté de la cinquième combinaison sont les lettres « u », « z »
et « t ».
Lorsque les élèves ont déterminé les ouvertures, distribuer les boîtes à souliers et les ciseaux et leur demander de créer leur jeu. Rappeler les mesures de sécurité à suivre lorsqu’on utilise un instrument tranchant.
Laisser les élèves choisir la stratégie à utiliser pour tracer sur la boîte les formes des ouvertures. Par exemple, des élèves peuvent placer les pentacubes plats (individuels ou superposés) sur la boîte et en tracer le contour. D’autres peuvent découper les formes des ouvertures dessinées au préalable sur du papier quadrillé, puis tracer leur contour sur la boîte.
Demander aux élèves de préparer une présentation pour l’échange mathématique à l’aide de leur jeu ou d’une grande feuille. Préciser qu’elles et ils doivent expliquer la stratégie utilisée pour déterminer la forme des cinq ouvertures et présenter, s’il y a lieu, leurs découvertes mathématiques en utilisant des termes de causalité ou de conséquence logique (par exemple, « puisqu’il y a 12 pentacubes et seulement cinq ouvertures, alors certaines des ouvertures doivent permettre d’insérer plus de deux pentacubes »).
Après l’apprentissage (objectivation/échange mathématique)
Durée : environ 15 minutes
Inviter quelques équipes à venir faire une présentation au groupe-classe.
Inviter les autres élèves à poser des questions aux équipes qui présentent et à faire part de leurs observations. Faire progresser l’échange en posant des questions telles que :
- Qui peut m’expliquer dans ses mots la stratégie utilisée par cette équipe?
- Est-ce que d’autres équipes ont utilisé la même stratégie? Est-ce que cette stratégie vous semble efficace?
- Est-ce que d’autres équipes ont utilisé les cinq mêmes ouvertures?
- Comment peut-on justifier que deux ouvertures soient différentes?
- Quels concepts mathématiques étaient présents dans cette activité? (Deux ouvertures sont différentes si elles ne sont pas congruentes, c’est-à-dire qu’elles ne peuvent pas être superposées.)
En créant le jeu, les élèves utilisent, parfois inconsciemment, divers concepts mathématiques. Afin de déterminer la forme des ouvertures, elles et ils doivent tenir compte des concepts d’aire et de congruence. De plus, la manipulation des formes et des solides auxquels les élèves font subir diverses transformations favorise le développement d’habiletés liées à la visualisation.
Pour enrichir l’échange mathématique et établir un lien entre des concepts de Sens de l’espace et de Données, l’enseignante ou l’enseignante peut choisir de faire à ce moment l’activité « Des hexominos populaires ».
Après l’objectivation, demander aux élèves d’échanger leur jeu avec celui d’une autre équipe et d’insérer leurs 12 pentacubes à plat par l’une des cinq ouvertures de la boîte reçue. Les mettre au défi de réussir à les insérer tous du premier coup dans la bonne ouverture. Souligner qu’elles et ils doivent observer attentivement les formes des pentacubes et des ouvertures et visualiser l’ouverture dans laquelle il sera possible d’insérer un pentacube. Ce n’est qu’au moment où les élèves ont la certitude d’avoir repéré la bonne ouverture qu’elles et ils prennent le pentacube et tentent de l’insérer dans l’ouverture. Cette démarche permet aux élèves de développer leur habileté à visualiser des déplacements de formes dans l’espace.
Différenciation pédagogique
|
Pour faciliter la tâche |
Pour enrichir la tâche |
|
Note : Cette activité exige un degré plus élevé de visualisation.
Note : Les élèves se rendront compte qu’il est impossible de le créer à moins que la mesure de l’aire d’une des quatre ouvertures ne soit de 7 unités carrées. |
Suivi à la maison
Montrer aux élèves la figure 1 ci-dessous et leur demander lequel des cubes 1, 2 et 3 représente une transformation du cube modèle.
Figure 1
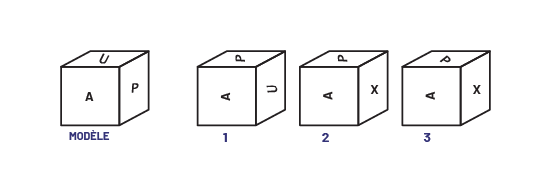 Image Il y a une série de cubes. Sous le premier cube est écrit: modèle. La vue de face du cube est
marquée par
un « a »; la vue du haut est marquée par un « u »; et la vue d’un côté est marquée par un « p ».À la droite du cube,
il y a trois autres cubes. La vue de face du premier cube est marquée par un « a »; la vue
du haut est marquée par un « p »; et la vue d’un côté est marquée par un « u ». La vue de face du second cube est
marquée par un « a »; la vue du haut est marquée par un « p »; et la vue d’un
côté est marquée par un « x ». La vue de face du troisième cube est marquée par un « a »; la vue du haut est marquée
par un « p »; et la vue
d’un côté est marquée par un « x ».
Image Il y a une série de cubes. Sous le premier cube est écrit: modèle. La vue de face du cube est
marquée par
un « a »; la vue du haut est marquée par un « u »; et la vue d’un côté est marquée par un « p ».À la droite du cube,
il y a trois autres cubes. La vue de face du premier cube est marquée par un « a »; la vue
du haut est marquée par un « p »; et la vue d’un côté est marquée par un « u ». La vue de face du second cube est
marquée par un « a »; la vue du haut est marquée par un « p »; et la vue d’un
côté est marquée par un « x ». La vue de face du troisième cube est marquée par un « a »; la vue du haut est marquée
par un « p »; et la vue
d’un côté est marquée par un « x ».
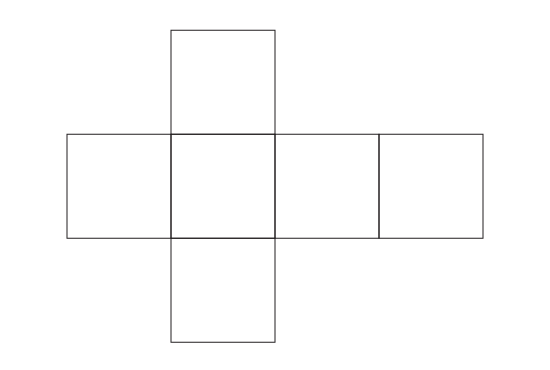
Inviter les élèves à créer un problème semblable à la maison et à demander à un membre de sa famille de le résoudre. Souligner l’importance de faire attention à l’orientation des lettres. Au besoin, remettre une copie des figures 2 et 3 ci-dessous. Des élèves pourraient choisir de construire un cube modèle à partir de la figure 3 et d’y inscrire une lettre sur chacune des faces pour les aider à déterminer la façon de placer les lettres sur les faces des cubes de la figure 2.
Figure 2

Figure 3
Activité : des hexominos populaires
Cette activité fait suite à la situation d’apprentissage « La boîte à pentacubes » et permet d’établir un lien entre des concepts des domaines Sens de l’espace et Données. Il s’agit de construire un tableau pour présenter l’éventail des ouvertures retenues par les équipes dans la construction de leur jeu et d’analyser les résultats obtenus.
Demander aux élèves de tracer et de découper la forme de chacune des cinq ouvertures de leur jeu. Préparer, sur de grandes feuilles, un tableau comme celui illustré ci-dessous sur lequel est inscrit le numéro ou le nom de chaque équipe.
 Image Un tableau constitué de 12 colonnes et huit rangées. La première rangée identifie les équipes
et la forme des ouvertures. Dans la deuxième rangée, il y a dix combinaisons de six carrés. Dans les quatre
prochaines rangées sont des « x » qui correspondent à l’équipe et la forme des ouvertures.
Image Un tableau constitué de 12 colonnes et huit rangées. La première rangée identifie les équipes
et la forme des ouvertures. Dans la deuxième rangée, il y a dix combinaisons de six carrés. Dans les quatre
prochaines rangées sont des « x » qui correspondent à l’équipe et la forme des ouvertures.
Afficher le tableau et demander à une équipe d’y placer la forme de l’une de leurs cinq ouvertures. Demander à toutes les équipes qui ont utilisé cette forme d’ouverture de tracer un X ou de placer un papillon adhésif sous celle-ci, dans la case de leur équipe y correspondant. Poursuivre cette démarche jusqu’à ce que les cinq ouvertures de toutes les équipes soient répertoriées dans le tableau. Faire le total du nombre d’utilisations de chaque ouverture.
Inciter les élèves à observer et à analyser les données au tableau. Poser diverses questions telles que :
- Quelles constatations pouvez-vous faire à partir des données présentées dans le tableau?
- Combien de formes d’ouverture différentes ont été utilisées dans la construction des jeux?
- Quelles ouvertures ont été utilisées le plus souvent?
- Toutes les équipes ont utilisé l’ouverture
 Image Figure faite de 6 carrés qui est semblable au développement d’un cube.
Quatre carrés forment une colonne. Un carré se place à la droite et un à la gauche du deuxième carré de la
colonne. ou l’ouverture
Image Figure faite de 6 carrés qui est semblable au développement d’un cube.
Quatre carrés forment une colonne. Un carré se place à la droite et un à la gauche du deuxième carré de la
colonne. ou l’ouverture  Image Figure faite de 6 carrés, sur 3 colonnes, de 2 carrés, 3 carrés, et un
carré. La colonne du milieu dépasse d’un carré.. Pourquoi? Qu’ont-elles de particulier? (Ce sont les deux
seules ouvertures qui permettent d’insérer le pentacube X.)
Image Figure faite de 6 carrés, sur 3 colonnes, de 2 carrés, 3 carrés, et un
carré. La colonne du milieu dépasse d’un carré.. Pourquoi? Qu’ont-elles de particulier? (Ce sont les deux
seules ouvertures qui permettent d’insérer le pentacube X.) - Les ouvertures
 Image Figure faite de 6 carrés, sur 2 colonnes, 2 carrés puis 4 carrés, sur la vertical. et
Image Figure faite de 6 carrés, sur 2 colonnes, 2 carrés puis 4 carrés, sur la vertical. et
 Image
Figure faite de 6 carrés, sur 3 colonnes, de 2 carrés dont la première est décalée d’un carré vers le haut.
ont été utilisées assez souvent. Qu’ont-elles de particulier? (Elles permettent d’insérer quatre pentacubes.)
Image
Figure faite de 6 carrés, sur 3 colonnes, de 2 carrés dont la première est décalée d’un carré vers le haut.
ont été utilisées assez souvent. Qu’ont-elles de particulier? (Elles permettent d’insérer quatre pentacubes.)
- Pourquoi certaines ouvertures sont-elles peu utilisées? (Ce sont probablement celles qui ne permettent d’insérer qu’un seul pentacube.)
- Combien d’équipes ont utilisé les cinq mêmes ouvertures?
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 65-76.
