E1.3 Effectuer des homothéties et décrire la similarité entre l’image et la figure initiale.
ACTIVITÉ 1 : EFFECTUER DES HOMOTHÉTIES
a) Fais subir une homothétie de rapport 2 au triangle ci-dessous et décris la similarité entre l’image et la figure initiale.
b) Sur une feuille de papier quadrillé, trace un triangle dont les côtés mesurent respectivement 6 cm, 8 cm et 10 cm. Situe un point O à l’extérieur de ton triangle. Trace des segments qui partent du point O et qui joignent chacun des sommets du triangle ABC comme dans l’exemple ci-dessous.
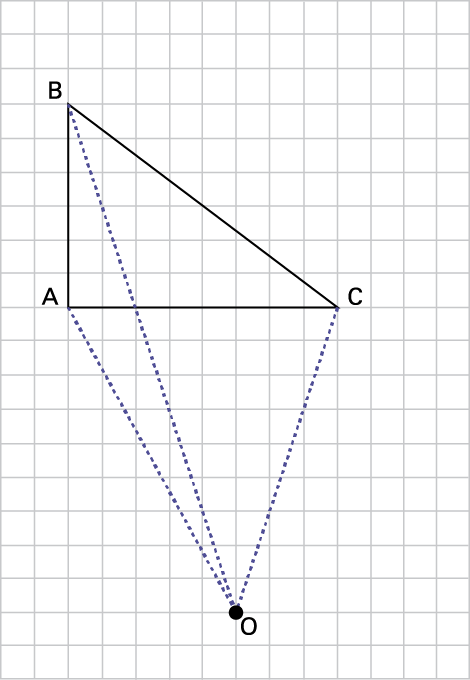
Fais subir une homothétie de rapport \(\frac{1}{2}\) à ta figure initiale et tires-en des conclusions.
Réponses possibles
a) Pour chaque sommet ABC, je trace une droite qui relie chaque point au centre d’homothétie. À l’aide d’une règle, je mesure la distance entre chaque sommet de la figure et le centre d’homothétie. Je multiplie ensuite chacune des distances par le rapport d’homothétie 2. Par exemple, je mesure la longueur du segment OA. Le segment OA' mesure 4 cm. Je trace alors un segment OA' de 8 cm pour former le segment OA' en passant par le point A, car le rapport d’homothétie est de 2. Je reprends la même démarche pour former les segments OB' et OC'.
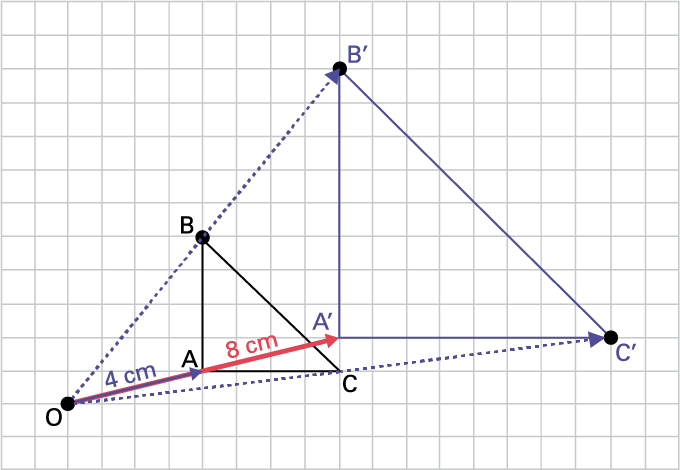image Sur
un quadrille, un triangle « A » « B » « C » est dessiné. Un peu en décalage est dessiné le triangle « A » prime, « B »
prime, « C » prime. Un point « O » est placé de façon à pouvoir enligné sur une droite les points « O » « A » « A »
prime, mais aussi « o » « b » « B » prime et, « O » « C » « C » prime.
Cette homothétie représente une transformation qui a pour effet d’agrandir la figure initiale selon le rapport donné. Je remarque que les côtés du triangle A'B'C' sont deux fois plus longs que ceux du triangle ABC. De plus, la distance entre l’origine (point O) et les sommets de l’image est 2 fois plus grande que la distance entre l’origine et les sommets de la figure initiale. Les figures ont la même forme, mais sont de taille différente. Les deux figures sont proportionnelles. Leurs angles restent les mêmes, et la longueur de leur côté est agrandie suivant le rapport d’homothétie.
b) Pour chaque sommet ABC, je trace une droite qui relie chaque point au centre d’homothétie. À l’aide d’une règle, je mesure la distance entre chaque sommet de la figure et le centre d’homothétie. Je divise ensuite chacune des distances par le rapport d’homothétie \(\frac{1}{2}\). Par exemple, je mesure la longueur du segment entre O et A. Le segment OA mesure 5 cm. Je trace alors un point sur le segment à 2,5 cm pour former le segment OA'. Je reprends la même démarche pour former les segments OB' et OC'.
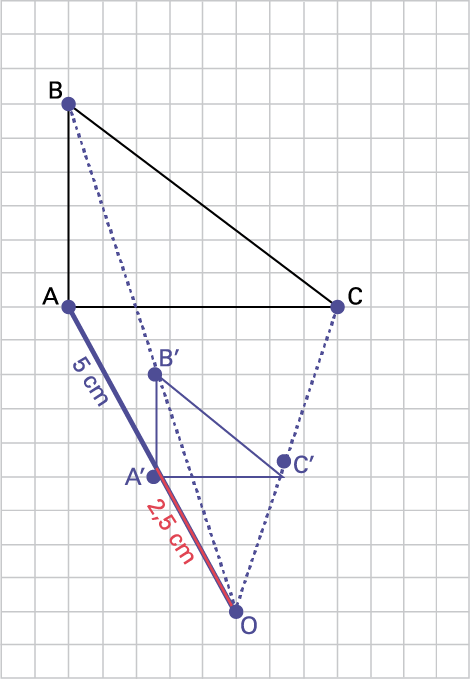image Sur un quadrille, un triangle « A » « B » « C » est dessiné. Un
peu en décalage est dessiné le triangle « A » prime, « B » prime, « C » prime. Un point « O » est placé de façon à
pouvoir enligné sur une droite les points « O » « A » « A » prime, mais aussi « o » « b » « B » prime et, « O » « C »
« C » prime.
Cette homothétie représente une transformation qui a pour effet de réduire la figure initiale selon le rapport donné, soit \(\frac{1}{2}\). Je remarque que les côtés du triangle A'B'C' sont deux fois plus courts que ceux du triangle ABC. De plus, la distance entre l’origine et les sommets de l’image est deux fois plus petite que la distance entre l’origine et les sommets de la figure initiale. Les figures ont la même forme, mais sont de taille différente. Les deux figures sont proportionnelles. Leurs angles restent les mêmes, et la longueur de leur côté est réduite suivant le rapport d’homothétie.
Source : En avant les maths!, 7e année, CM, Sens de l’espace, p. 5-7.
ACTIVITÉ 2 : DÉCRIRE DES HOMOTHÉTIES
a) Trouve le rapport d’homothétie que le triangle a subi en tenant compte du centre d’homothétie.
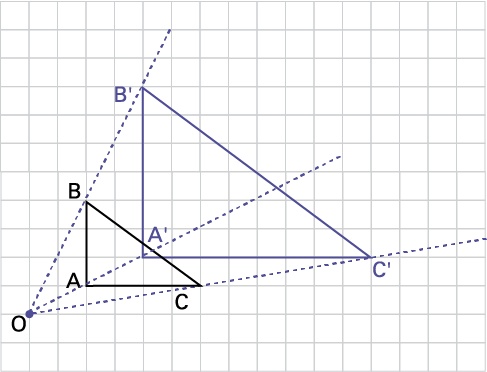image Sur
un quadrille, un triangle « A » « B » « C » est dessiné. Un peu en décalage est dessiné le triangle « A » prime, « B »
prime, « C » prime. Un point « O » est placé de façon à pouvoir enligné sur une droite les points « O » « A » « A »
prime, mais aussi « o » « b » « B » prime et, « O » « C » « C » prime.
b) Observe ces deux figures. Que remarques-tu?
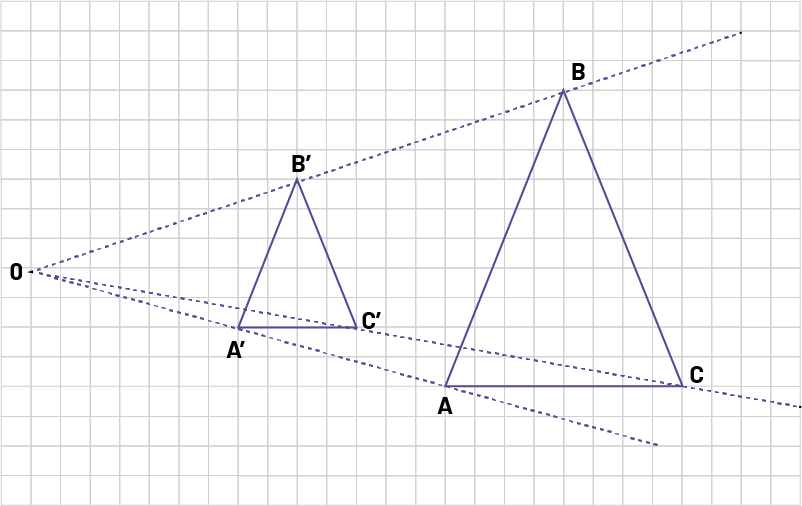image Sur un quadrille, un triangle « A » « B » « C » est dessiné. Un
peu en décalage est dessiné le triangle « A » prime, « B » prime, « C » prime. Un point « O » est placé de façon à
pouvoir enligné sur une droite les points « O » « A » « A » prime, mais aussi « o » « b » « B » prime et, « O » « C »
« C » prime.
Source : En avant les maths!, 7e année, ML, Sens de l’espace, p. 17.