E2.1 Décrire la différence et la similarité entre le volume et la capacité, et résoudre des problèmes en se servant de la relation entre les millilitres (ml) et les centimètres cubes (cm3).
ACTIVITÉ 1 : ACTIVITÉ EXPLORATOIRE SUR LES OBJETS QUI PEUVENT ÊTRE UTILISÉS COMME UNITÉS DE MESURE DE VOLUME
But
Dans cette activité, les élèves découvrent plusieurs objets qui peuvent être utilisés comme unités de mesure de volume.
Matériel
- boîtes de céréales
- boîtes de souliers
- boîtes à cadeaux de diverses dimensions
- cubes emboîtables
- récipients circulaires tels que des boîtes circulaires de croustilles, des rouleaux de papier essuie-tout.
Démarche
Remettre aux élèves plusieurs objets communs (par exemple, boîtes de céréales, boîtes de souliers, boîtes à cadeaux de diverses dimensions, cubes emboîtables, récipients circulaires).
Discuter avec les élèves du choix de l’unité de mesure de volume à utiliser.
Inviter les élèves à estimer le volume de chaque objet selon l’unité de mesure choisie (en utilisant un repère).
Leur demander de déterminer le volume approximatif de chacun en construisant, à l’aide d’objets plus petits, un solide qui occupe approximativement le même espace.
Note : Encourager les élèves à utiliser diverses formes à trois dimensions comme unités de mesure de volume. Elles et ils réaliseront que l’utilisation de cubes permet une meilleure estimation de l’espace occupé par un solide en forme de prisme.
Exemples
- Pour construire un solide qui occupe approximativement le même espace qu’une grosse boîte, on a utilisé 80 boîtes de céréales.
- Pour construire un solide qui occupe approximativement le même espace qu’un contenant de balles de tennis, on a utilisé trois rouleaux de papier essuie-tout.
- Pour construire un solide qui occupe le même espace qu’une boîte de mouchoirs de papier, on a utilisé 264 cubes emboîtables.
Source : L'@telier - Ressources pédagogiques en ligne (atelier.on.ca).
ACTIVITÉ 2 : ACTIVITÉ EXPLORATOIRE SUR LES OBJETS QUI PEUVENT ÊTRE UTILISÉS POUR LA CONSTRUCTION DE STRUCTURES DE VOLUME DONNÉ
But
Dans cette activité, les élèves construisent des solides ayant une mesure de volume donné.
Matériel
Cubes emboîtables
Démarche
Demander aux élèves de construire un décimètre cube à l’aide du matériel de base 10.
Inviter les élèves à estimer le volume de gros objets à l’aide du décimètre cube construit.
Exemples de gros objets
- Un bac de recyclage (approximativement 60 dm3)
- Un sac d’école (environ 24 dm3)
Les élèves devront être en mesure d’expliquer la démarche utilisée afin d’obtenir leur approximation. Voici des pistes de questionnement pour les guider :
- Comment avez-vous fait afin d’arriver à votre approximation?
- Quelles stratégies avez-vous utilisées?
Demander aux élèves de construire des solides de volumes exprimés en dm3.
Exemples de solides
- Un solide ayant un volume de 10 dm3.
- Un solide ayant un volume de 7 dm3.
Demander aux élèves de montrer à leurs pairs le solide construit.
Elles et ils peuvent échanger leurs solides et vérifier si le volume demandé a été respecté.
Source : L'@telier - Ressources pédagogiques en ligne (atelier.on.ca).
ACTIVITÉ 3 : ACTIVITÉS DE MESURE DE LA CAPACITÉ AVEC DES UNITÉS CONVENTIONNELLES – UN DÉCIMÈTRE CUBE
But
Cette activité permet de construire un décimètre cube pour développer le sens de ce que représente un litre.
Matériel
- feuille de papier quadrillé métrique (voir annexe 1)
- ciseaux, ruban gommé
- carton rigide
- récipient d’un litre (un par équipe)
- matériel de remplissage sec (riz, sable, maïs non éclaté, etc.)
Démarche
Demander aux élèves de découper dans du carton cinq carrés dont chaque côté mesure 1 dm (utiliser au besoin des quadrillages en cm2).
Leur demander de coller les carrés pour former le décimètre cube. Il n’est pas nécessaire d’avoir la face du dessus.
Leur dire de s’assurer que les mesures intérieures du cube ainsi formé sont toutes de 1 dm.
Les élèves doivent remplir le décimètre cube avec le matériel de remplissage.
Leur proposer de comparer ce contenu avec le contenu d’un récipient d’un litre.
Poser la question : « Quelle est la relation entre la capacité d’un contenant de 1 dm3 et la capacité d’un contenant d’un litre? ».
Note : Il faut éviter de dire qu’un décimètre cube est égal à un litre. Il faut plutôt dire que 1 dm3 est équivalent à 1 l ou qu’un récipient de 1 dm3 a la même capacité qu’un récipient de 1 l.
Source : L'@telier - Ressources pédagogiques en ligne (atelier.on.ca).
ACTIVITÉ 4 : RELATION ENTRE LES UNITÉS DE MESURE DE CAPACITÉ, DE MASSE ET DE VOLUME – CAPACITÉ, MASSE, VOLUME
But
Cette activité permet aux élèves d’établir une relation entre les unités de mesure de capacité, de masse et de volume si l’objet est de l’eau pure à 4 °C sous pression normale. Par exemple, 1 litre d’eau pure a une masse de 1 kg et occupe le même espace que 1 dm3.
|
Capacité |
Masse |
Volume |
|
1 ml |
1 g |
1 cm3 |
|
1 l |
1 kg |
1 dm3 |
|
1 kl |
1 t |
1 m3 |
Matériel
- un récipient d’un litre
- un décimètre cube
- une balance à plateaux et des masses de 1 g, de 1 mg et de 1 kg
- eau pure (distillée) à 4 °C (L’eau du robinet à température ambiante est acceptable pour cette activité.)
- riz, haricots ou sable
Démarche
Inviter les élèves à vérifier, à l’aide du riz, des haricots ou du sable, si le contenu du récipient d’un litre occupe le même espace que le décimètre cube.
Demander aux élèves de justifier leur réponse.
Réponse : Oui. Quand je remplis le récipient d’un litre avec du riz et que je verse ce contenu dans le décimètre cube, c’est la même quantité.
Demander aux élèves d’expliquer le lien entre la capacité d’un récipient d’un litre et le volume d’un cube dont chaque arête mesure 1 dm.Réponse : C’est la même chose. Un litre d’eau remplit exactement le décimètre cube.
Inviter les élèves à déterminer, à l’aide de la balance à plateaux, la masse d’un litre d’eau et à expliquer leur démarche.
Réponse : Je détermine la masse du contenant vide à l’aide des masses. Je remplis le contenant d’eau et je détermine de nouveau sa masse. La quantité de masses ajoutées correspond à la masse du litre d’eau ou la différence entre la masse du contenant plein et celle du contenant vide.
Leur poser ensuite les questions suivantes.
Note : Pour cette activité, il faut allouer aux élèves une certaine marge d’erreur à cause des objets utilisés.
- Quelle est la masse, en kg, d’un litre d’eau?
Réponse : La masse d’un litre d’eau est de 1 kg.
- Quelle quantité d’eau est contenue dans 1 dm3?
Réponse : La quantité d’eau contenue dans 1 dm3 est de 1 litre.
- Quelle est la masse de la quantité d’eau contenue dans 1 dm3?
Réponse : La masse de la quantité d’eau contenue dans 1 dm3 est de 1 kg.
- Quel est le lien entre la masse, en kg, d’un litre d’eau, la capacité du récipient et l’espace occupé par cette quantité d’eau? Comment le sais-tu?
Réponse : Les trois mesures sont équivalentes. 1 l = 1 kg = 1 dm3.
- Quel est le lien entre les unités de mesure de capacité, de masse et de volume si on a 1 g d’eau? 1 kl d’eau?
Réponse : Un millilitre d’eau a une masse de 1 g et un volume de 1 cm3. Un kilolitre d’eau a une masse de 1 tonne et un volume de 1 m3.
- Est-ce que les liens entre le ml, le cm3 et le g seraient les mêmes avec un autre liquide que l’eau (huile, savon liquide, etc.)?
Réponse : La plupart du temps, non. Plusieurs liquides n’ont pas la même densité que l’eau. La masse de 1 l de savon liquide sera plus grande que 1 kg.
Mise en garde : L’élève peut expérimenter avec d’autres liquides et conclure que le lien entre 1 ml, 1 cm3 et 1 g n’existe pas avec du savon liquide ou de l’huile. Il ne faut toutefois pas s’attendre à ce qu’elle ou il comprenne les raisons à cet âge.
- Est-ce que ce rapport reste le même si on utilise du riz? des haricots? du sable? Comment le sais-tu?
Réponse : Non, parce que ces produits sont plus lourds que l’eau. La masse de 1 l de riz sera plus grande que 1 kg.
Mise en garde : L’élève peut
Source : L'@telier - Ressources pédagogiques en ligne (atelier.on.ca).
ACTIVITÉ 5 : ACTIVITÉS DE MESURE DE VOLUMES AVEC DES UNITÉS CONVENTIONNELLES – LE MÈTRE CUBE
Sommaire
Cette activité permet aux élèves de construire la charpente d’un cube dont chaque côté mesure 1 m.
Matériel
- deux grandes feuilles de tableau de conférence par équipe de trois
- mètres
- ruban adhésif
Démarche
Faire des rouleaux dont la longueur est d’un mètre ou plus. Si on plie la feuille de papier assez serré à partir d’un coin, le rouleau formé est plus rigide que si on ne fait qu’enrouler la feuille pour former un tube.
Note : Il faut 12 feuilles pour chaque cube.

S’assurer que chaque rouleau mesure au moins 1 m de longueur. Replier les bouts si cela est nécessaire.
Joindre les rouleaux à l’aide de ruban adhésif afin de former un cube dont les arêtes mesurent 1 m de longueur. Le cube formé a un volume de 1 m3.
Source : L'@telier - Ressources pédagogiques en ligne (atelier.on.ca).
ACTIVITÉ 6 : ACTIVITÉS DE MESURE DE VOLUMES AVEC DES UNITÉS CONVENTIONNELLES – PETITS CUBES DU MATÉRIEL DE BASE 10
But
Cette activité permet aux élèves de déterminer le volume de divers objets à l’aide de petits cubes du matériel de base 10.
Matériel
- petites boîtes de diverses dimensions
- cubes emboîtables
- petits cubes du matériel de base 10 (en grande quantité)
- récipients circulaires
Démarche
Remettre aux élèves plusieurs objets communs (par exemple, petites boîtes de diverses dimensions, cubes emboîtables, petits cubes du matériel de base 10, récipients circulaires).
Inviter les élèves à estimer le volume de chaque objet si l’unité de mesure est le centimètre cube (le petit cube).
Demander aux élèves de déterminer le volume de chaque objet en construisant un solide qui occupe approximativement le même espace à l’aide de petits cubes du matériel de base 10. Par exemple, pour construire un solide qui occupe approximativement le même espace qu’un paquet de cartes à jouer, on a utilisé 126 petits cubes.
Source : L'@telier - Ressources pédagogiques en ligne (atelier.on.ca).
ACTIVITÉ 7 : ACTIVITÉ DE MESURE POUR LE FOYER – QUEL ESPACE CE SOLIDE OCCUPE-T-IL?
Matériel
- 14 petits cubes (matériel de base 10)
- cubes emboîtables de 2 cm × 2 cm × 2 cm
Démarche
Parent
Donner six petits cubes (1 cm × 1 cm × 1 cm) à votre enfant et lui demander de construire une tour d’une hauteur de six cubes.
Lui demander le volume de cette tour (l’espace qu’occupe cette tour).
Réponse : La tour a un volume de 6 centimètres cubes ou 6 cm3.
Lui demander d’estimer si le cube emboîtable (de 2 cm × 2 cm × 2 cm) occupe un plus grand ou un plus petit espace que la tour construite (sans préciser que le cube mesure 2 cm × 2 cm × 2 cm).
Laisser l’enfant calculer et tirer ses propres conclusions.
Attention! Votre enfant doit réaliser que le volume d’un prisme plus long peut être plus petit que celui d’un cube dont les arêtes sont plus courtes.
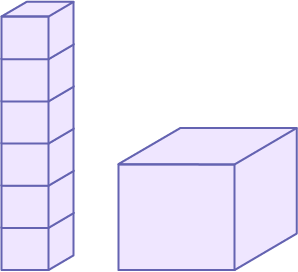
Le volume de la tour de six petits cubes est 1 × 1 × 6 × 1 cm3 ou 6 cm3.
Le volume du gros cube est 2 × 2 × 2 × 1 cm3 ou 8 cm3.
Les arêtes du gros cube sont pourtant plus courtes que la longueur de la tour.
Comment un prisme plus court peut-il avoir un plus gros volume?
Enfant
Elle ou il construit la tour de 6 cm3 et détermine son volume.
Elle ou il estime si un cube emboîtable (de 2 cm × 2 cm × 2 cm) a un plus grand ou un plus petit volume que la tour.
Elle ou il construit un cube de 2 cm × 2 cm × 2 cm pour vérifier son estimation.
Elle ou il tire une conclusion et justifie sa réponse.
Source : L'@telier - Ressources pédagogiques en ligne (atelier.on.ca).
Considération lors d’activités de volume avec des blocs
Volume : L’élève peut représenter un centimètre cube en se référant, par exemple, au petit cube venant du matériel de base 10. Il est préférable qu’elle ou il ne recoure pas aux cubes emboîtables, puisque certains de ces cubes mesurent 2 cm de long; leur volume est donc de 8 cm3 plutôt que de 1 cm3. Lorsqu’elle ou il comprend que 1 cm3 est équivalent à 1 ml, cela l’aide à mieux visualiser cette quantité en l’associant à la capacité d’une bouteille d’eau. Le mètre cube est plus difficile à estimer. L’élève peut représenter un mètre cube en l’associant, par exemple, au volume d’un appareil électroménager, comme une machine à laver.
Source : Guide d’enseignement efficace des mathématiques de la 7e à la 10e année, p. 45.
ACTIVITÉ 8 : ACTIVITÉ SUR L’ATTRIBUT VOLUME - UN VOLUME, C’EST QUOI?
But
Dans cette activité, les élèves font la distinction entre le volume d’un récipient et sa capacité.
Matériel
- contenants transparents de différents formats et capacités
- eau
- verre thermos
- tasses à mesurer de capacités diverses
Démarche
Demander aux élèves de déterminer la capacité d’un verre thermos à l’aide d’une tasse à mesurer.
Note : Il est important que le récipient choisi ait une paroi assez épaisse pour que l’activité soit efficace et ne crée pas de confusion chez l’élève.
Dans un plus gros contenant rempli d’eau à ras bord, submerger le verre thermos et récupérer l’eau qui a débordé. OU Dans un plus gros contenant d’eau sur lequel on a fait un trait vis-à-vis du niveau de l’eau, submerger le verre thermos et faire un second trait vis-à-vis du niveau de l’eau.
Mesurer la quantité d’eau qui a débordé ou qui s’est déplacée à l’aide d’une tasse à mesurer.
Comparer la quantité d’eau qui a débordé ou qui s’est déplacée (soit le volume du verre thermos) et la capacité du verre thermos.
Faire remarquer aux élèves la différence entre le volume du verre thermos (la quantité d’eau qui a débordé ou qui s’est déplacée) et la capacité de ce verre (la quantité d’eau qu’il peut contenir).
Source : L'@telier - Ressources pédagogiques en ligne (atelier.on.ca).
ACTIVITÉ 9 : Capacité ou volume
Former des équipes de deux, puis leur remettre un thermos fermé et un récipient gradué suffisamment grand pour y immerger le thermos. Leur demander de déterminer le volume et la capacité du thermos et d’utiliser les résultats pour expliquer la différence entre ces deux attributs.
Lorsque toutes les équipes ont terminé, regrouper les élèves et discuter des stratégies utilisées et des résultats obtenus. Faire ressortir le fait que le volume du thermos est plus grand que la capacité parce qu’il correspond au volume extérieur du thermos, alors que la capacité correspond au volume intérieur.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 168.
ACTIVITÉ 10 : Vide ou pleine? Avec ou sans bouchon?
Dans un premier temps, montrer aux élèves deux bouteilles identiques et fermées, l’une vide et l’autre pleine.
Leur poser la question suivante : « D’après vous, si on immerge ces deux bouteilles dans un récipient d’eau, laquelle va déplacer le plus grand volume d’eau? Pourquoi? ».
Note : Quelques élèves auront peut-être tendance à croire que la bouteille pleine va déplacer un plus grand volume d’eau que la bouteille vide parce qu’elle a une plus grande masse.
Former des équipes de deux, mettre à leur disposition le matériel nécessaire (par exemple, bouteille vide, bouteille pleine, récipient gradué, eau) et leur demander de vérifier leur réponse à l’aide de la stratégie de leur choix.
Lorsque toutes les équipes ont terminé, regrouper les élèves et discuter des stratégies utilisées et des résultats obtenus. Inciter les élèves à conclure que le volume d’eau déplacée par les deux bouteilles est le même parce qu’elles occupent le même espace. Elles ont donc le même volume.
Dans un deuxième temps, montrer aux élèves deux bouteilles identiques et vides, l’une avec un bouchon et l’autre sans bouchon, puis leur poser la question suivante : « D’après vous, si on immerge ces deux bouteilles dans un récipient d’eau, laquelle va déplacer le plus grand volume d’eau? Pourquoi? ».
Note : Quelques élèves auront peut-être tendance à croire que les deux bouteilles vont déplacer le même volume d’eau parce que les deux sont vides.
Former des équipes de deux, mettre à leur disposition le matériel nécessaire (par exemple, bouteille avec bouchon, bouteille sans bouchon, récipient gradué, eau) et leur demander de vérifier leur réponse à l’aide de la stratégie de leur choix.
Lorsque toutes les équipes ont terminé, regrouper les élèves et discuter des stratégies utilisées et des résultats obtenus. Inciter les élèves à conclure que la bouteille avec bouchon déplace un plus grand volume d’eau que la bouteille sans bouchon parce qu’elle occupe un plus grand espace.
De fait, le volume d’eau déplacé par la bouteille avec bouchon correspond à l’espace occupé par ses parois et par l’air à l’intérieur de la bouteille, alors que le volume d’eau déplacé par la bouteille sans bouchon correspond à l’espace occupé par ses parois seulement.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 169.
