La vue d'ensemble

À vue d'oeil...

un remaniement des guides d'enseignement efficace en mathématiques

FrançaisEnglish

E2.7 Démontrer que le volume d’un prisme ou d’un cylindre peut être calculé en multipliant l’aire de la base par sa hauteur, et se servir de cette relation pour calculer l’aire de la base, le volume et la hauteur de prismes et de cylindres lorsque deux des trois mesures sont connues.

ACTIVITÉ 1 : VOLUME D’UN PRISME DROIT À BASE RECTANGULAIRE

But

Cette activité permet de faire réaliser à l’élève qu’on détermine le volume d’un prisme en construisant un solide qui occupe le même espace que le prisme.

Matériel

  • divers prismes à base rectangulaire (boîte de chaussures, boîte de céréales, etc.).
  • beaucoup de cubes emboîtables de 1 cm sur 1 cm.
Démarche

Former des équipes de deux.

Remettre un prisme et une assez grande quantité de cubes emboîtables à chaque équipe.

Demander aux élèves de reproduire le prisme avec leurs cubes.

Poser les questions suivantes :

  • Quelle unité de mesure avez-vous utilisée pour reproduire le prisme?
  • Combien de centimètres cubes a-t-il fallu pour reproduire la longueur du prisme?
  • Combien de centimètres cubes a-t-il fallu pour en reproduire la largeur?
  • Combien de centimètres cubes a-t-il fallu pour en reproduire la hauteur?
  • Quelles sont les dimensions de votre prisme?
  • Quel est son volume en centimètres cubes?
  • Quelle est la relation entre les dimensions de votre prisme et son volume?
  • Comment peut-on déterminer le volume de n’importe quel prisme?

Exemple de réponse d’une équipe qui a un prisme de 5 cm sur 4 cm sur 3 cm : Sur la longueur, on peut placer cinq unités de volume de 1 cm3. Sur la largeur, on peut placer quatre unités de volume de 1 cm3. On a donc une base dont l’aire mesure 5 × 4 unités de mesure. Sur la hauteur, on peut placer trois unités de volume de 1 cm3. Donc, le volume de la boîte est de 5 × 4 × 3 unités de mesure (cm3), soit 60 cm3.

Note : Faire réaliser aux élèves que déterminer le volume d’un prisme, c’est déterminer l’aire de sa base (5 × 4 unités de mesure) et la multiplier par sa hauteur (trois unités de mesure). Donc, le volume d’un prisme peut s’exprimer comme ceci :

\(V = aire \ de \ la \ base \times hauteur\)

Source : L'@telier - Ressources pédagogiques en ligne (atelier.on.ca).

ACTIVITÉ 2 : VOLUME D’UN PRISME DROIT À BASE TRIANGULAIRE

Sommaire

Grâce à cette activité, l’élève pourra déterminer le volume d’un prisme droit à base triangulaire à l’aide de la formule pour calculer le volume d’un prisme droit.

Matériel 

  • une règle par équipe
  • une équerre ou un goniomètre par équipe
  • des prismes à base triangulaire
  • des feuilles de papier blanches, un crayon et une gomme à effacer.

Note : Un logiciel de codage pourrait être utilisé pour calculer le volume de prismes à partir de la formule.

Démarche

Former des équipes de deux.

Remettre aux équipes un prisme à base triangulaire.

Demander aux élèves d’indiquer les bases du prisme.

Leur demander de tracer le contour de la base du prisme sur une feuille de papier.

À l’aide d’une équerre, elles et ils tracent la hauteur du triangle et la mesurent en centimètres (2 cm).

Poser les questions ci-dessous.

Voici un exemple avec un prisme.

Un prisme à base triangulaire. La mesure du côté rectangle est 5 centimètres sur 8 centimètres. La hauteur de la base triangulaire est de 2 centimètres et la mesure d’un des côtés est 5 centimètres.
  • Quelle est la longueur de la base du triangle? 
    • Réponse attendue : La longueur de la base du triangle est de 5 cm.
  • Quelle est l’aire du triangle? 
    • Réponse attendue : Puisque l’aire d’un triangle est la base multipliée par la hauteur et divisée par 2, alors l’aire du triangle est \(\frac{5 \times 2}{2}\), soit 5. Donc, l’aire du triangle est de 5 cm2, car l’unité d’aire est le cm2.
  • Quelle est la hauteur du prisme? 
    • Réponse attendue : La hauteur du prisme est de 8 cm.
  • Comment détermine-t-on le volume d’un prisme? 
    • Réponse attendue : L’aire de la base multipliée par sa hauteur.
  • Quel est le volume de ton prisme? 
    • Réponse attendue : Puisque la hauteur du prisme est de 8 cm, alors le volume est \(\begin{align} V &= 5 \ cm^{2} \times 8 \ cm \\ &= 40 \ cm^{3} \end{align} \)
      Donc, le volume du prisme est de 40 cm3.
Activité d’enrichissement

  1. Trouver ou construire une boîte ayant la forme d’un prisme droit à base triangulaire (la boîte d’une marque de chocolat suisse bien connue).

  2. Déterminer le volume de la boîte.

Source : L'@telier - Ressources pédagogiques en ligne (atelier.on.ca).

ACTIVITÉ 3 : VOLUME DE GROS OBJETS

Sommaire

Dans cette activité, l’élève détermine le volume de gros objets à l’aide de l’unité de mesure de volume la plus appropriée.

Matériel 

  • un mètre par équipe
  • un décimètre cube par équipe
  • une liste d’objets qui ne sont pas tous des prismes (par exemple, une cabane, un réservoir à eau chaude, une poubelle, un dictionnaire, le pupitre du personnel enseignant)
Démarche

Former des équipes de deux.

Demander aux élèves de mesurer les longueurs nécessaires pour déterminer le volume des objets à l’aide de la formule qu’elles et ils ont découverte dans les activités précédentes. Les élèves peuvent aussi construire un solide qui occupe approximativement le même espace.

Source : L'@telier - Ressources pédagogiques en ligne (atelier.on.ca).

ACTIVITÉ 4 : CALCUL DE LA HAUTEUR D’UN PRISME À PARTIR DE L’AIRE ET DE SON VOLUME

Voici deux solides ayant chacun un volume de 126 dm3. Détermine la hauteur de chaque prisme.

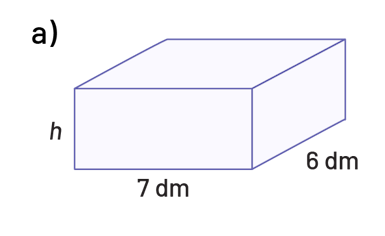
Prisme rectangulaire dont la largeur du côté est 7 décimètres et la longueur du côté est 6 décimètres. La hauteur est « h ».

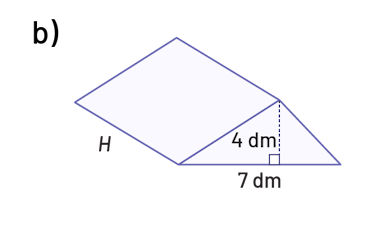
Un prisme à base triangulaire, la hauteur est « H ». La longueur de la base est 7 décimètres.

Source : En avant, les maths!, 7e année, ML, Sens de l’espace, p. 21.

ACTIVITÉ 5 : CALCUL DU VOLUME D’UN CYLINDRE

Trouve le volume de ce cylindre.

Un cylindre dont le rayon mesure 3 virgule 5 centimètres. La hauteur du cylindre est de 8 centimètres.

Une structure est formée d’un prisme droit à base trapézoïdale surmonté d’un cube. Détermine le volume de la structure.

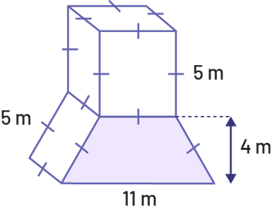
Un prisme droit à base trapézoïde surmonté d’un cube. Tous les côtés du cube sont égaux et mesurent 5 mètres. La hauteur du trapèze est de 4 mètres, sa longueur est de 11 mètres, en bas et 5 mètres en haut, et sa largeur est de 5 mètres.

Source : En avant, les maths!, 7e année, ML, Sens de l’espace, p. 22-23.

ACTIVITÉ 6 : AIRE ET VOLUME DE SOLIDES

Détermine l’aire de la base, puis le volume de chacun des prismes suivants.

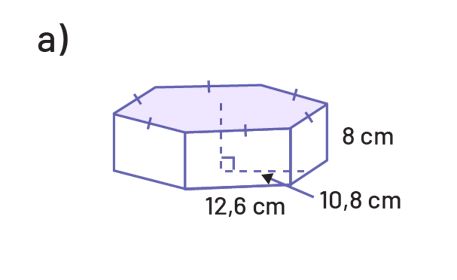
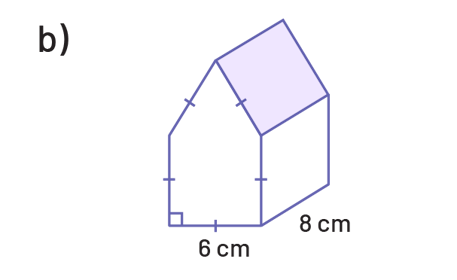
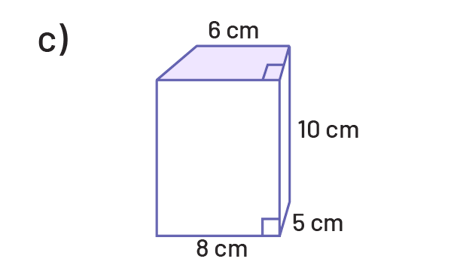
Prisme à base hexagonale. Les côtés de l’hexagone mesures tous 12 virgule 6 centimètres. La hauteur du prisme est 8 centimètres. Et la distance du bord du prisme et du point central est de dix virgule 8 centimètres. Un prisme pentagonal « en forme de maison ». Les 5 côtés du pentagone sont égaux et mesurent 6 centimètres. La hauteur est de 8 centimètres. Un prisme à base à base rectangulaire. Le rectangle de la base mesure 8 centimètres sur 5 centimètres. La hauteur du prisme est de dix centimètres. 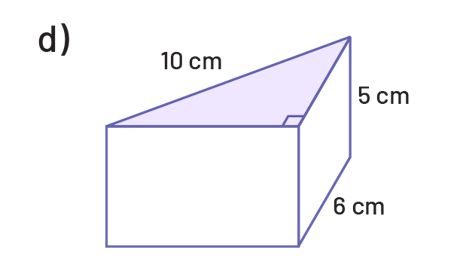Un prisme à base triangulaire. Le triangle de la base est un triangle avec un angle droit, le côté opposé à l’angle droit est de dix centimètres. Un autre côté du triangle mesure 6 centimètres, la hauteur est de 5 centimètres. 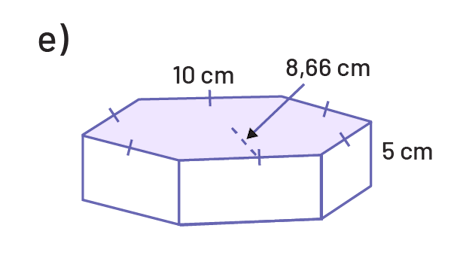Prisme à base hexagonale. Les côtés de l’hexagone mesures tous dix virgule 6 centimètres. La hauteur du prisme est 5 centimètres. Et la distance du bord du prisme et du point central est de 8 virgule 66 centimètres.

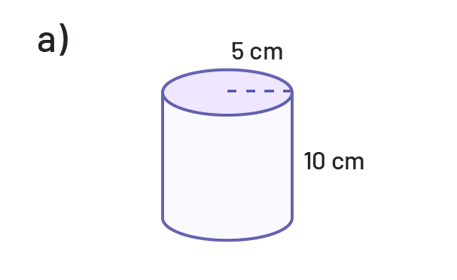
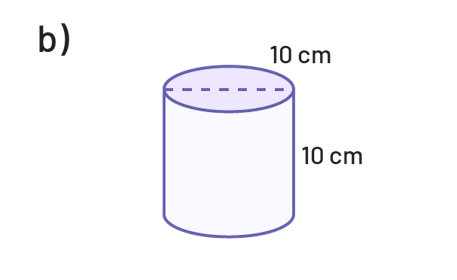
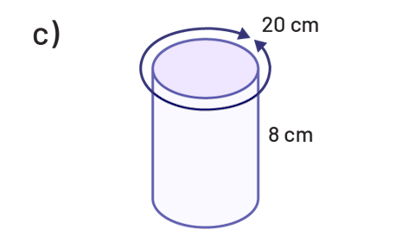
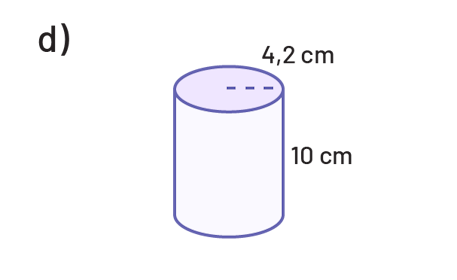
Détermine l’aire de la base, puis le volume de chacun des cylindres suivants.

Cylindre dont la hauteur est dix centimètres. Le rayon de la base circulaire est de 5 centimètres. Cylindre dont la hauteur est dix centimètres. Le diamètre de la base circulaire est de dix centimètres. Cylindre dont la hauteur est 8 centimètres. La circonférence de la base circulaire est de 20 centimètres. Cylindre dont la hauteur est dix centimètres. Le rayon de la base circulaire est de 4 virgule 2 centimètres.

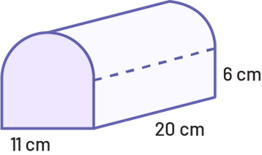
La partie supérieure de chaque extrémité du pain ci-dessous a la forme d’un demi-cercle. Détermine le volume du pain. Montre ton travail.

Un prisme qui a la forme d’un pain arrondi sur le dessus, avec une base rectangulaire de 11 centimètres par 20 centimètres. Une ligne pointillée détermine le début du demi-cercle. Du début du demi-cercle à la base rectangulaire il y a 6 centimètres.

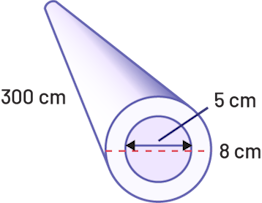
Un tuyau mesurant 300 cm de long a un diamètre extérieur de 8 cm et un diamètre intérieur de 5 cm. Quel volume de matériau faut-il pour le fabriquer? Montre ton travail.

Un tuyau dont le diamètre de l’espace vide intérieur a un diamètre de 5 centimètres., le diamètre total du tuyau est de 8 centimètres. La hauteur du tuyau est de 2 décimètres.

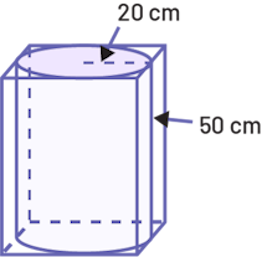
Détermine le volume intérieur de la plus petite boîte en forme de prisme à base carrée dans laquelle on peut insérer le cylindre ci-dessous.

Un cylindre rentre exactement dans un prisme à base carrée. La hauteur du cylindre est de 50 centimètres. Le rayon de la base circulaire est de 20 centimètres.

Source: Réduction des écarts de rendement, 9e année, p. 10-11 et 15-16.