E1.2 Tracer les vues de face, de côté et de dessus, ainsi que de diverses perspectives, d’objets et d’espaces physiques, selon des échelles appropriées.
HABILETÉ : TRACER LES VUES AINSI QUE DIVERSES PERSPECTIVES D’OBJETS ET D’ESPACES PHYSIQUES, SELON DES ÉCHELLES APPROPRIÉES
Les solides peuvent être illustrés graphiquement en deux dimensions. Les représentations bidimensionnelles montrent la façon dont des objets sont faits et dont ils peuvent être analysés ou reproduits. Elles peuvent être utilisées pour représenter de très petits objets comme de très grands espaces. Plusieurs métiers (par exemple, conception, construction, urbanisme, illustration d’instruction) se servent de ces représentations bidimensionnelles.
Afin d’assurer l’exactitude des reproductions des dessins techniques en trois dimensions, il faut se servir des vues de dessus (plans) ainsi que des vues de face et de côté (élévations), et des « dessins plats » sans perspectives.
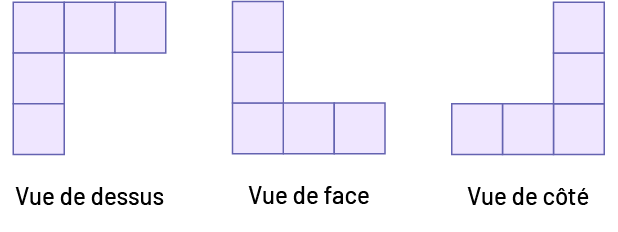 image Vue de dessus: 5 blocs sont placés de façon à former un « L » à l’envers. Vue de face : 5 blocs sont placés de façon à former un « L ». Vue de côté : 5 blocs sont placés de façon à former un « L » dont l’ouverture est vers la droite.
image Vue de dessus: 5 blocs sont placés de façon à former un « L » à l’envers. Vue de face : 5 blocs sont placés de façon à former un « L ». Vue de côté : 5 blocs sont placés de façon à former un « L » dont l’ouverture est vers la droite.Il est également important de tracer un dessin à l’échelle afin de reproduire les proportions de l’élément initial, c’est-à-dire les angles et les distances relatives.
Lorsque les trois vues sont montrées au sein d’une même illustration, on parle de dessin en perspective. Puisque les dessins en perspective sont souvent plus faciles à comprendre que ceux qui ne le sont pas, ils sont habituellement privilégiés pour les illustrations. Deux des types de dessin en perspective utilisés sont la projection isométrique et la projection oblique (ou cabinet).
Il est à noter que les vues en perspective ne montrent pas le côté arrière, de sorte que certains éléments peuvent être cachés. Ces vues représentent mieux les arêtes droites que les courbes. Elles peuvent déformer les angles et les dimensions de l’objet (longueur, hauteur et profondeur) pour obtenir l’effet de perspective désiré.
Le papier isométrique (ou papier quadrillé à triangles équilatéraux) est utile pour tracer des projections isométriques et obliques de façon approximative (l’échelle sera légèrement déformée). Pour donner l’effet de perspective sur ce type de papier, la projection isométrique fait glisser chaque sommet par un même vecteur de translation (par exemple, 5 vers la droite, 1 vers le haut), et la projection oblique fait glisser la face de devant par un même vecteur de translation (par exemple, 5 vers la droite, 1 vers le haut) et fait joindre les sommets.
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
Stratégies afin de tracer les différentes vues d’un solide
Exemple 1
L’élève doit tracer la vue de face, la vue de côté et la vue de dessus du solide ci-dessous. La flèche indique la vue de face du solide.
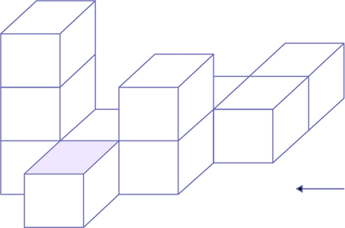
STRATÉGIE
Tracer les vues de face, de côté et de dessus selon des échelles appropriées.
L’élève reproduit d’abord le solide à l’aide de cubes emboîtables afin de l’aider à mieux représenter les différentes vues. Elle ou il veut représenter les différentes vues du solide en utilisant ses mesures réelles. À l’aide d’une règle, l’élève mesure les dimensions d’un cube emboîtable : \(1 \ cm \times 1 \ cm \times 1 \ cm\), et utilise donc l’échelle 1 : 1, soit 1 cm = 1 cm pour tracer les différentes vues du solide.

Exemple 2
L’élève doit observer attentivement ce solide et le représenter en réalisant deux dessins en perspective : la projection isométrique et la projection oblique (cabinet).

Projection isométrique
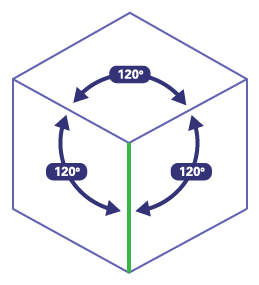
L’élève représente les trois dimensions du solide à l’aide de la projection isométrique. Pour réaliser son dessin, elle ou il utilise du papier isométrique parce que ce papier est formé de droites verticales et obliques reproduisant des angles de 120°. Il sera très utile pour dessiner les arêtes du solide.

Une projection isométrique représente un objet en perspective selon « une vue de coin ». L’élève trace donc le solide de manière que les arêtes (hauteur, largeur, profondeur) forment des angles de 120°. Elle ou il représente une arête en avant-plan.
L’élève utilise l’échelle 1 : 2 pour dessiner le solide, soit 1 cm = 2 cm pour représenter la longueur, la hauteur et la profondeur du solide. Chaque dimension de l’objet est représentée selon une échelle constante. Chaque dimension a la même mesure, soit 2 cm.

Projection oblique
La projection oblique représente un objet en perspective selon « une vue directe » de l’une de ses faces de manière que la profondeur soit représentée par des droites obliques (c’est-à-dire selon un angle). L’élève utilise donc du papier isométrique pour produire cette projection.
Pour réaliser son dessin, l’élève choisit une face à partir de laquelle elle ou il dessinera sa projection oblique.

Dans une projection oblique, la longueur et la hauteur ont une échelle égale. L’élève utilise donc une échelle de 1 : 2. Pour chaque centimètre en longueur ou en hauteur, elle ou il trace 2 cm sur le papier isométrique.
En ce qui a trait à la profondeur, l’échelle doit être la moitié de la mesure de la longueur et de la hauteur. Elle ou il utilise alors l’échelle 1 : 1, soit 1 cm = 1 cm.
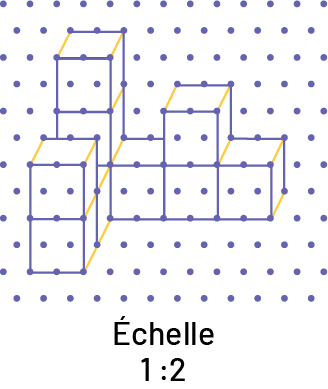
Source : En avant les maths 7e année, CM, Sens de l’espace, p. 4-7.
CONNAISSANCE : VUES DE FACE, DE CÔTÉ ET DE DESSUS
Les vues. Les vues de dessus (plans) ainsi que les vues de face et de côté (élévations) sont des « dessins plats » sans perspective.
 image Vue de dessus: 5 blocs sont placés de façon à former un « L » à l’envers. Vue de face : 5 blocs sont placés de façon à former un « L ». Vue de côté : 5 blocs sont placés de façon à former un « L » dont l’ouverture est vers la droite.
image Vue de dessus: 5 blocs sont placés de façon à former un « L » à l’envers. Vue de face : 5 blocs sont placés de façon à former un « L ». Vue de côté : 5 blocs sont placés de façon à former un « L » dont l’ouverture est vers la droite.Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
CONNAISSANCE : PERSPECTIVES ET ÉCHELLES APPROPRIÉES
Dessin à l’échelle. Dessin dans lequel les longueurs sont proportionnellement réduites ou augmentées par rapport aux longueurs réelles.
Dessin en perspective. Un dessin en perspective montre trois vues (vues de dessus, de face et de côté) au sein d’une même illustration. Les deux types de dessin en perspective sont la projection isométrique et la projection oblique (ou cabinet).
Projection isométrique. Elle représente un objet en perspective selon une « vue de coin » de manière que les arêtes principales de l’objet (c’est-à-dire les trois dimensions de l’objet) forment des angles égaux. Dans une projection isométrique, une échelle est appliquée de façon constante à toutes les dimensions de l’objet, par exemple, 1 cm = 2 cm pour la longueur, la hauteur et la profondeur.

Projection oblique (projection cabinet). Elle représente un objet en perspective selon une « vue directe » de l’une de ses faces de manière que la profondeur soit représentée par des droites obliques (c’est-à-dire selon un angle). Dans une projection oblique, l’échelle « de profondeur » est la moitié de l’échelle « de longueur et de hauteur ». Par exemple, si l’échelle pour la hauteur et la longueur est 1 : 2, soit 1 cm = 2 cm, alors l’échelle pour la profondeur est 0,5 : 2, soit 0,5 cm = 2 cm.
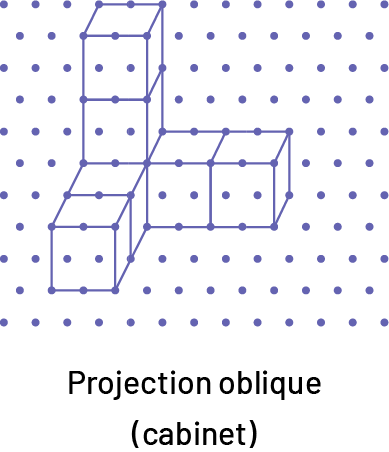
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
