À vue d'oeil...

E1.4 Décrire et effectuer des translations, des réflexions et des rotations dans un plan cartésien, et prédire les résultats de ces transformations.

HABILETÉ : DÉCRIRE ET EFFECTUER DES TRANSLATIONS

---

Les translations produisent des images congruentes. Une translation « fait glisser » une figure sur une distance donnée et dans une direction donnée (vecteur).

Lorsque des figures sont transformées dans un plan cartésien, on observe des régularités entre les coordonnées de la figure initiale et les coordonnées correspondantes de l’image. Il est particulièrement facile de décrire ces régularités quand le vecteur de translation (distance et direction) est comparé avec les coordonnées de la figure initiale et de l’image ayant subi une translation.

Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1^re à la 8^e année, 2020, Ministère de l’Éducation de l’Ontario.

Pour décrire et effectuer une translation oblique, par exemple, il faut vérifier à la fois le déplacement horizontal et le déplacement vertical. Pour ce faire, les élèves utilisent une notation symbolique entre parenthèses. Par exemple, une translation de trois unités vers la droite et de deux unités vers le bas est représentée symboliquement par (3D, 2B) ou (3, -2). Il est préférable d’habituer les élèves à décrire toujours la translation en indiquant d’abord le déplacement horizontal et ensuite le déplacement vertical.

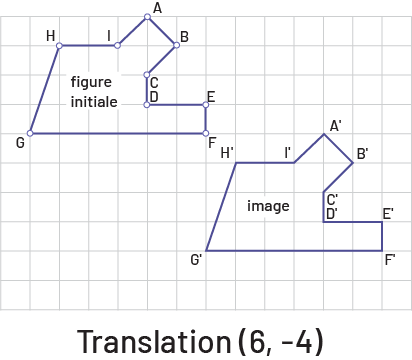
Les élèves peuvent décrire et effectuer des translations horizontales, verticales ou obliques définies à l’aide d’une flèche. Cette flèche peut être placée sur la figure ou à l’extérieur de la figure. La direction de la flèche correspond à la direction de la translation et sa longueur correspond à la grandeur du déplacement.

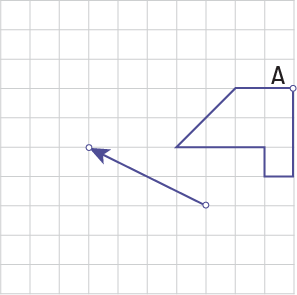
Pour décrire et effectuer la translation, les élèves doivent déterminer la grandeur des déplacements horizontaux et verticaux représentés par la flèche. Par exemple, la flèche ci-dessous définit la translation (-4, 2), soit un déplacement de quatre unités vers la gauche et de deux unités vers le haut.

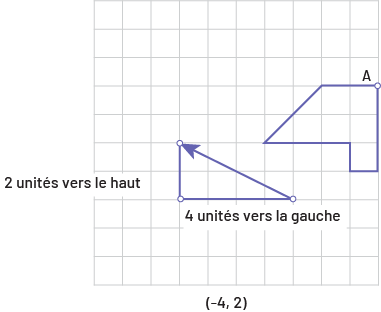
Lors d’une translation, tous les points de la figure initiale subissent le même déplacement, c’est-à-dire que tous les points de la figure initiale sont déplacés dans la même direction et sont équidistants des points correspondants de l’image.

image Une figure est sur un plan quadrillé. Une flèche indique la direction et la longueur de la translation. Dans ce cas si la translation sera de 2 unités vers le haut et 4 unités vers la gauche. Une deuxième figure représente la translation. « Chaque point de la figure initiale a subi une translation de 4 unités vers la gauche et de 2 unités vers le haut.

Source : Guide d’enseignement efficace des mathématiques de la 4^e à la 6^e année, p. 29-30.

Exemple 

Trace l’image d’une translation de (2, -3) de la figure ABCD. Décris l’effet de cette translation sur les coordonnées de l’image.

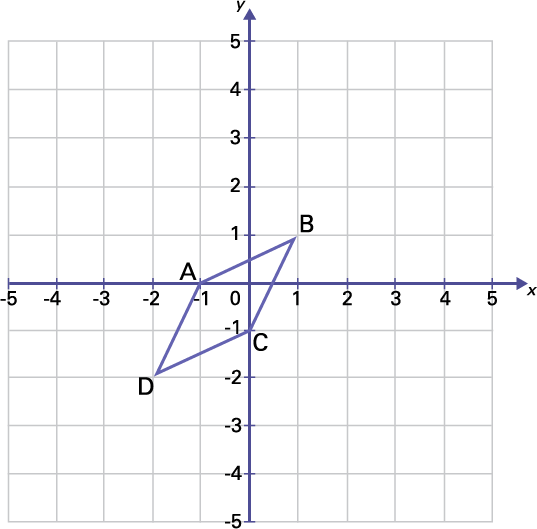image Sur un plan cartésien, l’ordonnée « y » est de 5 à moins 5, l’abscisse « X » est de moins 5 à 5. La figure « A » « B » « C » « D » est placée sur le plan cartésien. Le point « A » est à (parenthèse ouvrante )zéro, moins un (parenthèse fermante), le point « B » (parenthèse ouvrante ) un, un (parenthèse fermante, le point « C » est à (parenthèse ouvrante ) moins un, zéro (parenthèse fermante). Et le point « D » (parenthèse ouvrante) moins 2, moins 2 (parenthèse fermante).

Dans les coordonnées des points, la valeur de x augmente de 2 et la valeur de y diminue de 3.

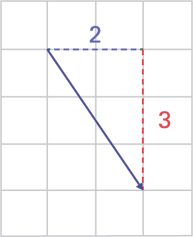
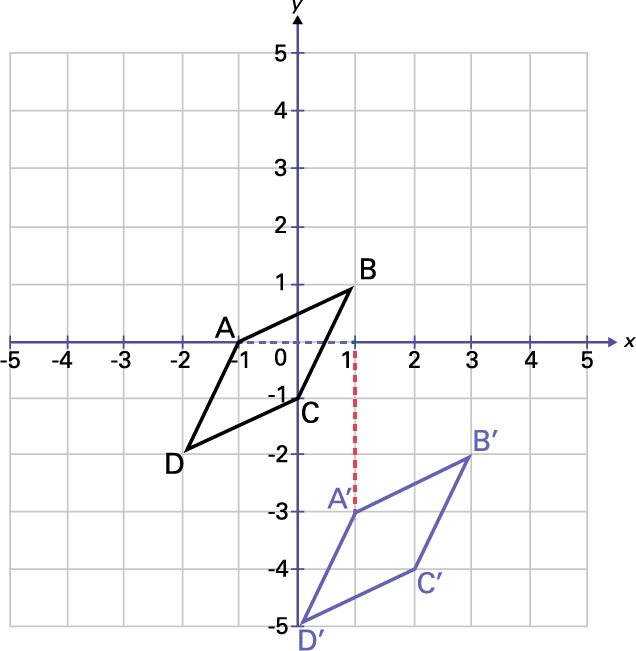image Sur un plan cartésien, l’ordonnée « y » est de 5 à moins 5, l’abscisse « X » est de moins 5 à 5. La figure « A » « B » « C » « D » est placée sur le plan cartésien. Le point « A » est à (parenthèse ouvrante) zéro, moins un (parenthèse fermante), le point « B » (parenthèse ouvrante) un, un (parenthèse fermante, le point « C » est à (parenthèse ouvrante) moins un, zéro (parenthèse fermante). Et le point « D » (parenthèse ouvrante) moins 2, moins 2 (parenthèse fermante). La translation du parallélogramme est « A » prime (parenthèse ouvrante) un, un (parenthèse fermante), « B » prime (parenthèse ouvrante) 3, moins 2 (parenthèse fermante), « C » prime (parenthèse ouvrante) 2, moins 4 (parenthèse fermante), « D » prime (parenthèse ouvrante) zéro, moins 5 (parenthèse fermante).

Figure initiale → image

(x, y) →  (x + 2, y – 3)

A (-1, 0) →  A' (1, -3)

B (1, 1) →  B' (3, -2)

C (0, -1) →  C' (2, -4)

D (-2, -2) →  D' (0, -5)

Je remarque que la translation « fait glisser » la figure initiale sur une distance donnée. J’observe aussi que l’image produite est congruente à la figure initiale. Je remarque également que lorsqu’il y a une translation vers la droite, la valeur de l’abscisse augmente et lorsqu’il y a une translation vers le bas, la valeur de l’ordonnée diminue.

Source : En avant les maths 7^e année, CM, Sens de l’espace, p. 8 et 9.

HABILETÉ : DÉCRIRE ET EFFECTUER DES RÉFLEXIONS

---

Une réflexion « inverse » une figure par rapport à un axe perpendiculaire à une direction donnée, appelé axe de réflexion, pour créer la figure opposée.

Lorsque des figures sont transformées dans un plan cartésien, on observe des régularités entre les coordonnées de la figure initiale et les coordonnées correspondantes de l’image. Il est particulièrement facile de décrire ces régularités quand une figure subit une réflexion par rapport à l’axe des x ou à l’axe des y.

Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1^re à la 8^e année, 2020, Ministère de l’Éducation de l’Ontario.

Pour décrire et effectuer une réflexion, il faut comprendre que tous les points sur la figure initiale et les points correspondants sur l’image sont à égale distance de l’axe de réflexion. La réflexion entraîne un changement de la position et de l’orientation initiale d’une forme, mais l’image réfléchie est congruente à l’original. En d’autres termes, l’image réfléchie a la même taille et la même forme, mais elle sera « orientée » dans une autre direction et se trouvera dans une autre position. Il est important de noter que l’axe de réflexion peut être tracé dans n’importe quelle direction par rapport à la forme originale (à horizontale, à la verticale ou en diagonale) selon n’importe quel angle.

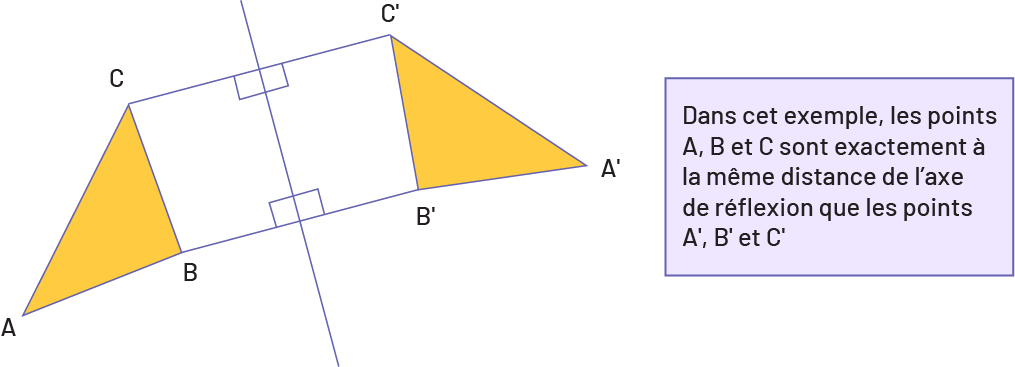image Un triangle « A » « B » « C » et sa réflexion, « A » prime, « B » prime, « C » prime. Des lignes de réflexion ont été placées entre « C » et « C » prime, et entre « B » et « B » prime. L’axe de réflexion est perpendiculaire à ces deux lignes. Dans un encadré, on peut lire : Dans cet exemple, les points « A », « B » , « C » sont exactement à la même distance de l’axe de réflexion que les points « A » prime, « B » prime, et « C » prime.

Source: Traduction de Guide to Effective Instruction in Mathematics, Kindergarten to Grade 6, p. 35.

Exemple 

a) Fais subir au triangle ABC une réflexion par rapport à l’axe des x.

Décris l’effet de cette réflexion sur les coordonnées de l’image.

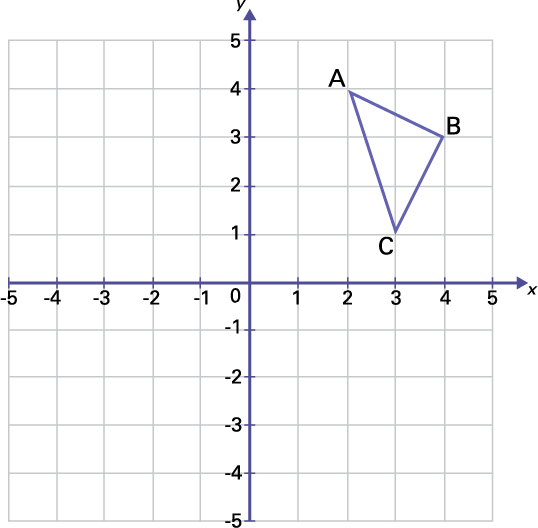image Un triangle « A » « B « C » est placé sur un plan cartésien aux coordonnées suivantes. « A » (parenthèse ouvrante) 2, 4 (parenthèse fermante), « B » (parenthèse ouvrante) 4, 3 ( parenthèse fermante), « C» (parenthèse ouvrante)3, un ( parenthèse fermante)

Réflexion par rapport à l’axe des x

Note : Lorsque l’élève découvre et aborde les différentes transformations, il est important qu’elle ou il puisse constater l’existence de liens entre les différentes transformations. Voici quelques questions pour amener l’élève à établir des liens.

• Que remarques-tu quant à l’image de la transformation?
• Y a-t-il d’autres transformations qui te permettraient d’obtenir la même image?
• Laquelle est, selon toi, la plus efficace? Pourquoi?

Dans les coordonnées des points, la valeur de l’ordonnée (y) devient l’opposé (change de signe), alors que la valeur de l’abscisse (x) reste la même.

Figure initiale →  image

(x, y) → (x, -y)

A (2, 4) → A' (2, -4)

B (4, 3) → B' (4, -3)

C (3, 1) → C' (3, -1)

Je remarque que la réflexion « inverse » la figure initiale par rapport à l’axe des x. J’observe que même si la figure A'B'C' n’a plus les mêmes coordonnées, la réflexion a reproduit une figure congruente à la figure initiale.

b) Fais subir au triangle ABC une réflexion par rapport à l’axe des y. Décris l’effet de cette réflexion sur les coordonnées de l’image.

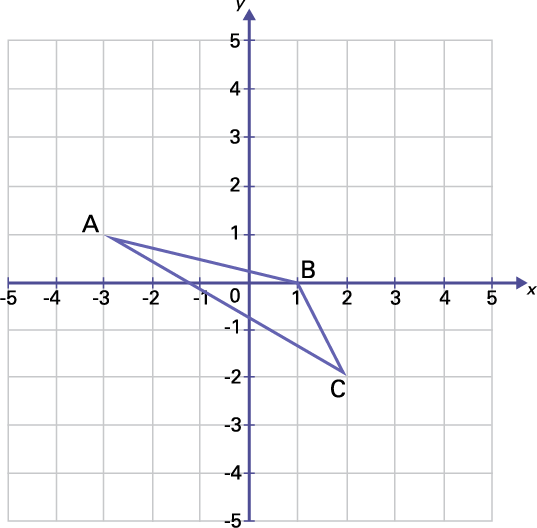image Un triangle « A » « B « C » est placé sur un plan cartésien aux coordonnées suivantes. « A » (parenthèse ouvrante) moins 3, un ( parenthèse fermante), « B » (parenthèse ouvrante) un, zéro ( parenthèse fermante), « C» (parenthèse ouvrante) 2, moins 2 ( parenthèse fermante)

Réflexion par rapport à l’axe des y

Dans les coordonnées des points, la valeur de l’abscisse (x) devient l’opposé (change de signe), alors que la valeur de l’ordonnée (y) reste la même.

Figure initiale →  image

(x, y) → (-x, y)

A (-3, 1) → A' (3, 1)

B (1, 0) → B' (-1, 0)

C (2, -2) → C' (-2, -2)

Je remarque que la réflexion « inverse » la figure initiale par rapport à l’axe des y. J’observe que même si la figure A'B'C' n’a plus les mêmes coordonnées, la réflexion a reproduit une figure congruente à la figure initiale.

Source : En avant les maths!, 7^e année, CM, Sens de l’espace, p. 10 à 13.

HABILETÉ : DÉCRIRE ET EFFECTUER DES ROTATIONS JUSQU’À 360° DANS UNE GRILLE

---

Une rotation « fait tourner » une figure autour d’un centre de rotation selon un angle donné.

Lorsque des figures sont transformées dans un plan cartésien, on observe des régularités entre les coordonnées de la figure initiale et les coordonnées correspondantes de l’image. Il est particulièrement facile de décrire ces régularités quand une figure subit une rotation de 90° ou de 180° autour du point d’origine (0, 0).

Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1^re à la 8^e année, 2020, Ministère de l’Éducation de l’Ontario.

Pour décrire et effectuer une rotation, il faut comprendre et indiquer :

1. l’emplacement du centre de rotation (par exemple, un point sur le contour de la figure, à l’intérieur de la figure ou à l’extérieur de la figure);

2. la mesure de la rotation (par exemple, un quart de tour, un demi-tour, trois quarts de tour);

3. le sens de la rotation (par exemple, dans le sens des aiguilles d’une montre, dans le sens contraire des aiguilles d’une montre).

Les élèves doivent comprendre ce que représente une rotation d’un quart de tour, d’un demi-tour et de trois quarts de tour dans le sens des aiguilles d’une montre ou dans le sens contraire des aiguilles d’une montre. Il est important de leur présenter diverses activités kinesthésiques qui leur permettent de développer cette compréhension.

L’utilisation de l’horloge (par exemple, une horloge en carton avec deux aiguilles fixées à l’aide d’une attache parisienne) est aussi une stratégie efficace pour aider les élèves à développer le sens des fractions de tour. Elles et ils placent d’abord les aiguilles à 12. Pour représenter une rotation d’un quart de tour dans le sens des aiguilles d’une montre, elles et ils déplacent l’aiguille des minutes à 3. L’aiguille des heures représente la direction initiale, alors que celle des minutes représente la direction après la rotation.

Les élèves peuvent établir le lien entre la fraction de tour de rotation de la grande aiguille d’une horloge, le nombre de minutes et le nombre de degrés. Par exemple, une rotation d’un quart de tour de la grande aiguille correspond à 15 minutes ou à 90°.

Note : Sur une véritable horloge, cette correspondance n’est pas tout à fait exacte puisque l’aiguille des heures se déplace légèrement lorsque l’aiguille des minutes effectue une rotation d’un quart de tour.

Il est à noter qu’il reste \(\frac{3}{4}\) de tour, ou 45 minutes, à faire pour que la grande aiguille située sur le 3 atteigne le 12.

Il importe encore une fois de varier la direction initiale des aiguilles. Par exemple, le personnel enseignant peut placer les deux aiguilles de l’horloge à 2 et demander aux élèves d’effectuer une rotation d’un demi-tour dans le sens des aiguilles d’une montre. Elles et ils peuvent alors comprendre qu’une rotation d’un demi-tour de la grande aiguille correspond à 180° ou à 30 minutes pour déterminer que l’aiguille des minutes doit être placée à 8.

Une fois que les élèves ont développé leur compréhension des fractions de tour à l’aide de matériel concret, elles et ils sont en mesure de les représenter sur des cercles tracés sur papier.

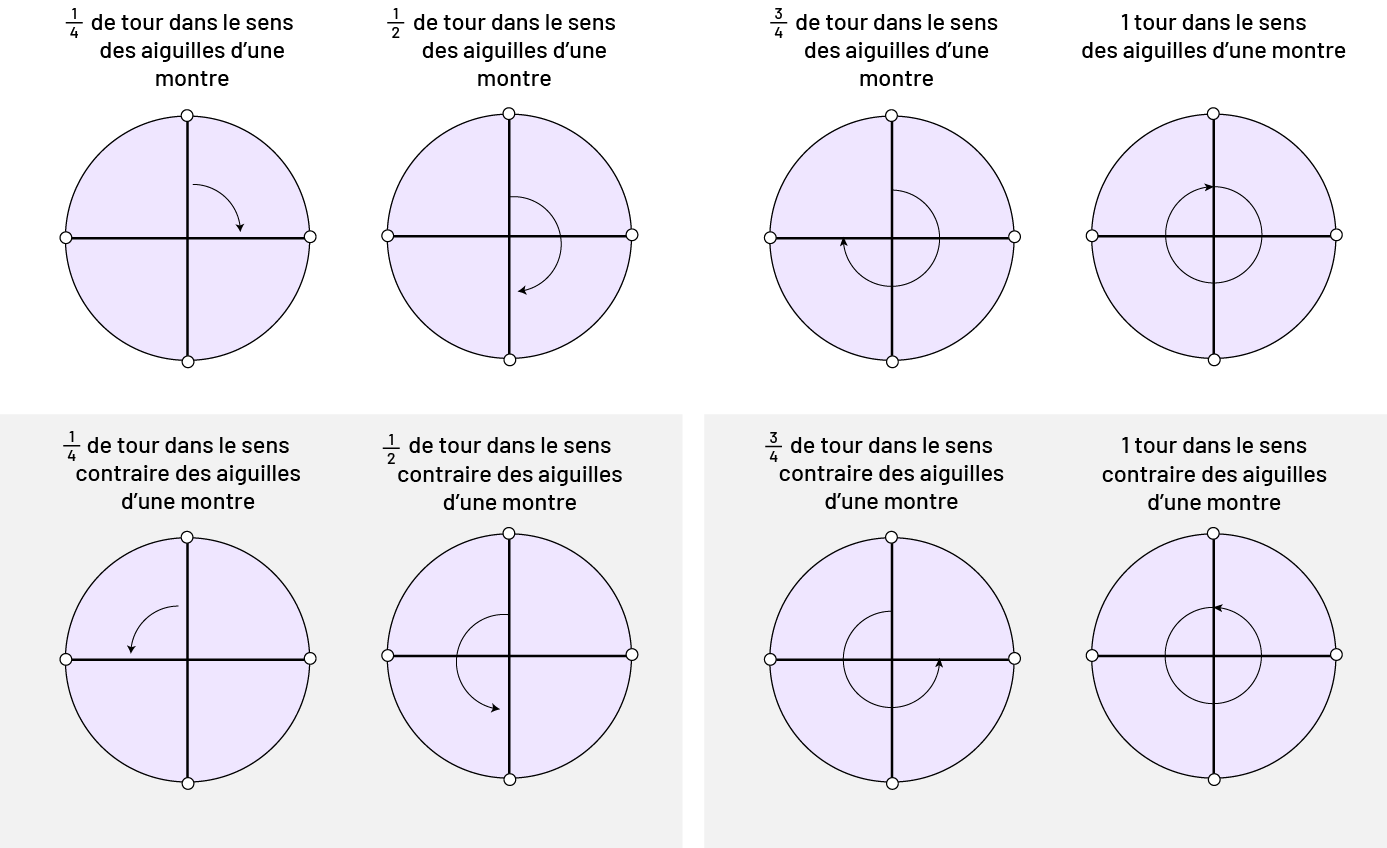image Une série de cercles cercle dont on a tracé l’axe horizontal et l’axe vertical, démontrent la rotation dans le sens des aiguilles d’une montre, un quart de tout, un demi-tour, trois quarts de tous et un tout. Une série de cercles cercle dont on a tracé l’axe horizontal et l’axe vertical, démontrent la rotation dans le sens contraire, des aiguilles d’une montre, un quart de tout, un demi-tour, trois quarts de tous et un tout.

Les élèves doivent effectuer des rotations de figures en utilisant un des sommets de la figure comme centre de rotation. L’utilisation de divers outils (par exemple, papier calque, papier à coordonnées polaires, équerre, logiciel) pour effectuer la rotation selon la fraction de tour précisée aide les élèves à mieux comprendre cette transformation. Les élèves effectuent aussi des rotations dont le centre est situé sur le contour, à l’intérieur de la figure et à l’extérieur de la figure.

Exemple 

Rotation d’un quart de tour dans le sens des aiguilles d’une montre, avec le centre de rotation :

• sur un sommet de la figure;

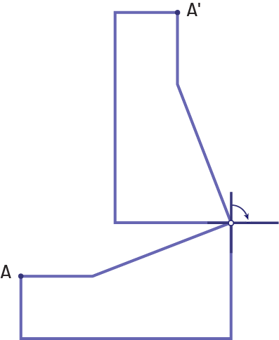
• sur le contour de la figure ou à l’intérieur de la figure;

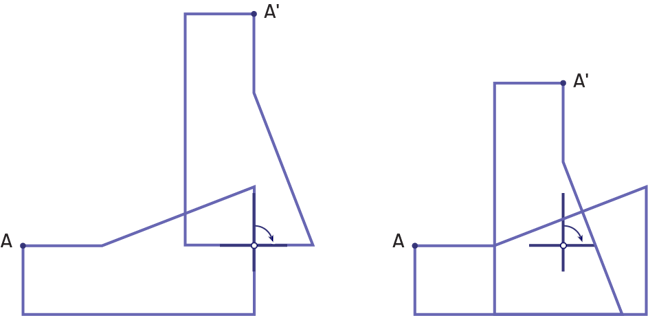
• à l’extérieur de la figure.

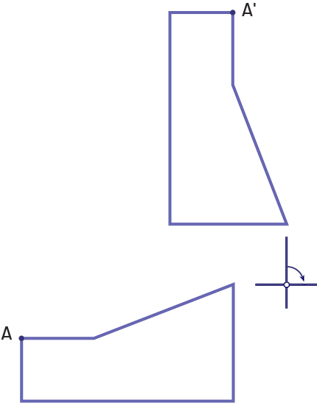
Source : Guide d’enseignement efficace des mathématiques de la 4^e à la 6^e année, p. 32-35.

Exemple

Rotation dans un plan cartésien selon un angle donné

Fais subir au triangle ABC une rotation de 90° et de 180° dans le sens des aiguilles d’une montre. Décris l’effet de ces rotations sur les coordonnées de l’image.

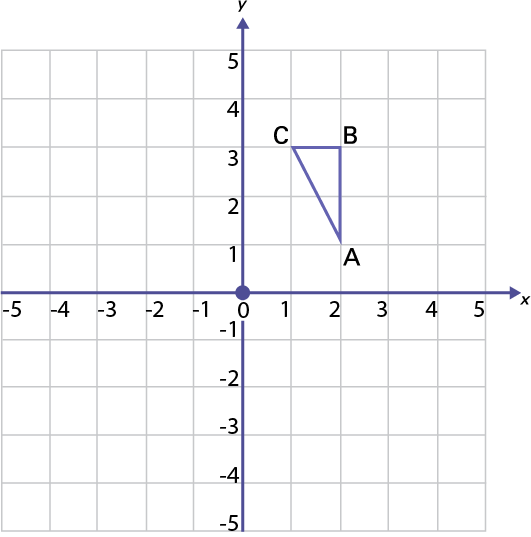
Je fais maintenant subir au triangle ABC une rotation de 90° (d’un quart de tour).

Dans les coordonnées des points, la valeur de l’ordonnée (y) et la valeur de l’abscisse (x) sont inversées et la valeur de l’ordonnée (y) devient l’opposé (change de signe).

Figure initiale → image

(x, y) → (y, -x)

A (2, 1) → A' (1, -2)

B (2, 3) → B' (3, -2)

C (1, 3) → C' (3, -1)

Je remarque que la rotation « fait tourner » la figure initiale autour d’un centre de rotation selon un angle donné. J’observe aussi que même si la figure A'B'C' n’a plus les mêmes coordonnées, la rotation a reproduit une figure congruente à la figure initiale.

Je fais maintenant subir au triangle ABC une rotation de 180° (d’un demi-tour). Dans les coordonnées des points, la valeur de l’abscisse (x) et la valeur de l’ordonnée sont l’opposé (changent de signe).

Figure initiale → image

(x, y) → (-x, -y)

A (2, 1) → A' (-2, -1)

B (2, 3) → B' (-2, -3)

C (1, 3) → C' (-1, -3)

Je remarque que la rotation « fait tourner » la figure initiale autour d’un centre de rotation selon un angle donné. La figure est inversée. J’observe aussi que même si la figure A'B'C' n’a plus les mêmes coordonnées, la rotation a reproduit une figure congruente à la figure initiale.

Source : En avant les maths!, 7^e année, CM, Sens de l’espace, p. 14 à 16.

HABILETÉ : PRÉDIRE LES RÉSULTATS DE TRANSLATIONS, DE RÉFLEXIONS ET DE ROTATIONS DANS UN PLAN CARTÉSIEN

---

Afin de pouvoir prédire les résultats de transformations, l’élève doit comprendre l’effet des transformations sur les coordonnées de chacun des points de la figure. Ainsi, ses prédictions seront fondées sur une réelle compréhension du concept de transformations.

Lorsque des translations, des réflexions et des rotations sont effectuées sur une figure, celle-ci garde ses dimensions (longueurs et angles) et n’est que placée différemment dans l’espace.

Contrairement aux homothéties, les translations, les réflexions et les rotations produisent des images congruentes.

Au cycle moyen, les élèves prédisent le résultat d’une transformation et décrivent ce qui arrivera à l’objet lorsque la transformation sera effectuée. Grâce à des recherches guidées, les élèves seront finalement capables d’observer l’orientation initiale d’un objet et le résultat d’une transformation, et de décrire la transformation effectuée sans avoir à la voir.

De plus, au départ, l’élève aborde les différentes transformations individuellement. Plus l’élève comprend leurs propriétés, plus elle ou il devrait être en mesure de constater qu’il existe des liens entre celles-ci. Une approche pédagogique flexible avec un questionnement qui permet à l’élève de réfléchir et d’établir des liens entre les différents types de transformations est à privilégier.

Voici quelques exemples de questions afin de guider l’élève dans son développement du raisonnement spatial :

• Que remarques-tu quant à l’image de la transformation?
• Y a-t-il d’autres transformations qui te permettraient d’obtenir la même image?
• Laquelle est, selon toi, la plus efficace? Pourquoi?
• Compare la translation avec les autres transformations apprises. Que remarques-tu?
• Quelles transformations pourraient avoir la même image?

Source : Traduction de A Guide to Effective Instruction in Mathematics, Kindergarten to Grade 6, p. 34.

CONNAISSANCE : TRANSLATION, RÉFLEXION, ROTATION, PLAN CARTÉSIEN (CONNAISSANCES ANTÉRIEURES)

---

Translation. Transformation dans laquelle chaque point d’une figure est déplacé à la même distance, dans la même direction, de façon à former une figure congruente, aussi appelée glissement.

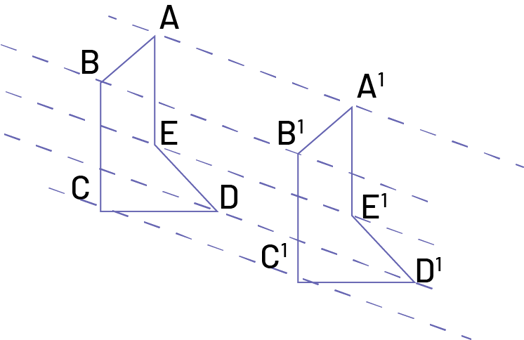
Source: Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1^re à la 8^e année, 2020, Ministère de l’Éducation de l’Ontario.

La translation est définie par sa grandeur et sa direction (représentées symboliquement par des coordonnées ou par une flèche). Elle représente un déplacement linéaire, horizontal, vertical ou oblique dans lequel la figure initiale et l’image sont congruentes. La distance entre chaque point sur la figure initiale et le point correspondant sur l’image est constante. L’orientation de l’image est la même que l’orientation de la figure initiale.

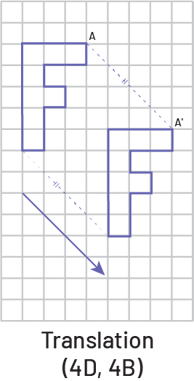
Source : Guide d’enseignement efficace des mathématiques de la 4^e à la 6^e année, p. 36 et 37.

Vecteur. Objet géométrique représenté par une flèche qui définit le sens, la direction et la distance d’une translation.

Réflexion. Symétrie par rapport à un axe perpendiculaire à une direction donnée.

Source: Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1^re à la 8^e année, 2020, Ministère de l’Éducation de l’Ontario.

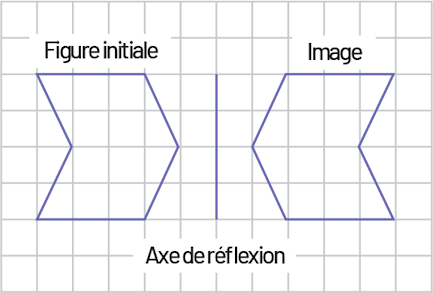
Une réflexion est un déplacement réflexif perpendiculaire à un axe de réflexion. Chaque point sur la figure initiale et le point correspondant sur l’image sont à la même distance de l’axe de réflexion. La figure initiale et l’image sont congruentes, mais l’orientation de l’image est différente de l’orientation de la figure initiale.

Source : Guide d’enseignement efficace des mathématiques, de la 4^e à la 6^e année, p. 36.

Rotation. Transformation selon laquelle chaque point d’une figure tourne autour d’un point fixe appelé centre de rotation, selon un angle de rotation donné.

Source: Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1^re à la 8^e année, 2020, Ministère de l’Éducation de l’Ontario.

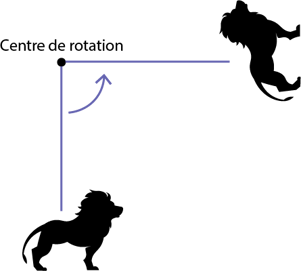
Une rotation est une transformation qui déplace chaque point d'une forme ou d'une figure autour d'un point fixe, appelé centre de rotation. Une rotation crée une image qui est congruente à la forme d'origine. Toutefois, l’orientation de l’image est différente de l’orientation de la figure initiale.

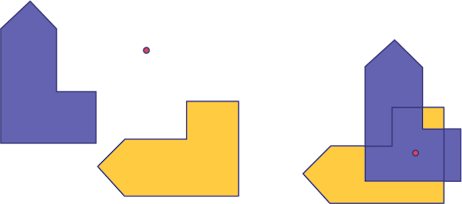
Le centre de rotation peut se retrouver n'importe où sur le plan, soit à l'extérieur de la figure, soit à l'intérieur.

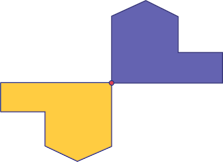
Lorsque le centre de rotation se retrouve sur un sommet de la figure, la figure initiale et son image partageront ce point.

Source : Traduction de A Guide to Effective Instruction in Mathematics, Kindergarten to Grade 6, p. 36.

Plan cartésien. Plan habituellement représenté par une surface plane divisée par deux droites perpendiculaires graduées, soit l’axe des abscisses (l’axe des x) et l’axe des ordonnées (l’axe des y). Aussi appelé grille des coordonnées cartésiennes ou plan des coordonnées.

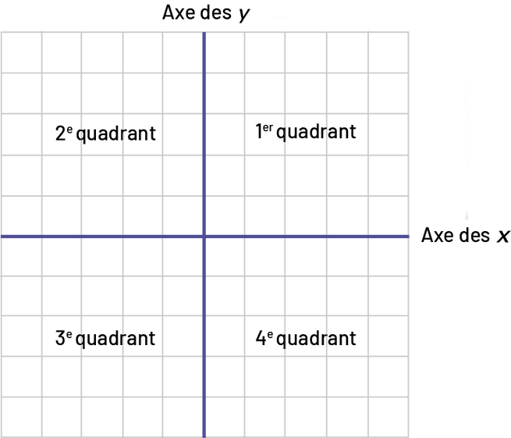
Source: Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1^re à la 8^e année, 2020, Ministère de l’Éducation de l’Ontario.