E2.1 Décrire la différence et la similarité entre le volume et la capacité, et résoudre des problèmes en se servant de la relation entre les millilitres (ml) et les centimètres cubes (cm3).
HABILETÉ : DÉCRIRE LA DIFFÉRENCE ET LA SIMILARITÉ ENTRE LE VOLUME ET LA CAPACITÉ
Le volume et la capacité décrivent des mesures tridimensionnelles. Le volume est la mesure de l’espace occupé par un objet. Si on place l’objet dans un contenant rempli d’eau et qu’on recueille l’eau déplacée par celui-ci lorsqu’on l’y insère, le nombre de ml (ou cm3) recueillis correspond au volume de l’objet. Pour des figures géométriques qui ne sont pas très complexes, il est possible de calculer ce volume avec des formules mathématiques.
Pour sa part, la capacité est le volume maximal que peut contenir un récipient. Donc, lorsqu’on parle de volume et de capacité d’un récipient, on parle respectivement du volume du contenant et de celui du contenu. Les deux se mesurent donc en ml ou en cm3.
Pour les volumes plus petits ou plus gros, l’élève verra des unités métriques différentes en 8e année.
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
HABILETÉ : RÉSOUDRE DES PROBLÈMES EN SE SERVANT DE LA RELATION ENTRE LES MILLILITRES (ML) ET LES CENTIMÈTRES CUBES (CM3)
En 7e année, les élèves doivent établir la relation d’équivalence entre un volume de 1 cm3 et un volume de 1 ml. Cette relation signifie, par exemple, que chaque millilitre d’eau dans un contenant quelconque occupe un espace de 1 cm3. Ainsi, si on verse 20 ml d’eau dans un contenant, l’eau occupera un espace de 20 cm3.
Une relation équivalente peut être établie en fonction d’unités de mesure plus grandes. On peut, par exemple, établir qu’un volume de 1 dm3 équivaut à un volume de 1 000 ml ou de 1 l.
Pour amener les élèves à bien comprendre cette relation, le personnel enseignant peut leur proposer deux activités : l’une fondée sur le concept de capacité d’un contenant, l’autre fondée sur le concept de volume d’un solide. Ces deux activités sont brièvement décrites dans les exemples ci-dessous. Dans chaque cas, il importe de laisser les élèves explorer la relation entre ces deux unités de mesure à l’aide d’expériences, de proposer une conjecture et de la vérifier.
Exemple 1 (capacité d’un contenant)
Remettre aux élèves un contenant dont il est facile de déterminer le volume intérieur (par exemple, contenant en plastique dont la forme est un prisme à base rectangulaire) ainsi qu’une éprouvette graduée en millilitres. Demander aux élèves de déterminer le volume intérieur du contenant, c’est-à-dire sa capacité, et de l’exprimer en cm3. Leur demander ensuite de remplir le contenant d’eau, puis de verser cette eau dans l’éprouvette graduée afin d’en déterminer le volume. Lors de l’échange mathématique, faire ressortir le fait que la mesure en cm3 correspondant à la capacité du contenant est très semblable à la mesure du volume d’eau en ml contenu dans l’éprouvette. Souligner que les petites différences entre ces mesures peuvent être attribuables au fait qu’il est difficile de remplir le contenant au maximum de sa capacité et de verser ensuite l’eau dans l’éprouvette sans en perdre.
Exemple 2 (volume d’un solide)
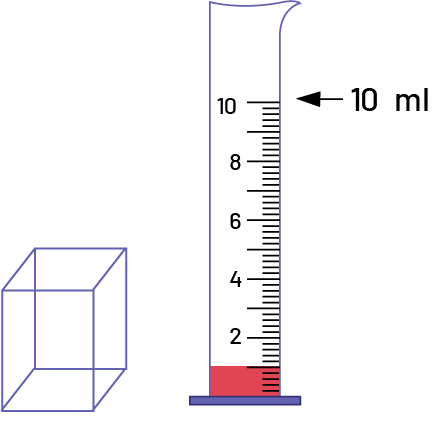
Remettre aux élèves un solide dont il est facile de déterminer le volume en centimètres cubes ainsi qu’une éprouvette graduée en millilitres. Leur demander de déterminer d’abord le volume du solide (en cm3), puis de verser une certaine quantité d’eau dans l’éprouvette et de noter le volume d’eau (en ml). Demander ensuite aux élèves de placer le solide dans l’éprouvette et de déterminer le volume d’eau qui a été déplacé. Lors de l’échange mathématique, faire ressortir le fait que la mesure, en cm3, correspondant au volume du solide est équivalente à la mesure, en ml, du volume d’eau déplacée. Inciter les élèves à conclure que chaque millilitre d’eau (1 ml) occupe un espace correspondant à un centimètre cube (1 cm3).
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 67-68.
Formules mathématiques pour calculer le volume de diverses figures géométriques
Note : Dans la formule pour mesurer le volume, \(V = A_{base} \times H\), la variable H majuscule représente la hauteur du prisme. La variable h minuscule, quant à elle, représente la hauteur du polygone qui forme la base du prisme.
Exemple :
Cube ou prisme droit à base carrée (ou à base rectangulaire)
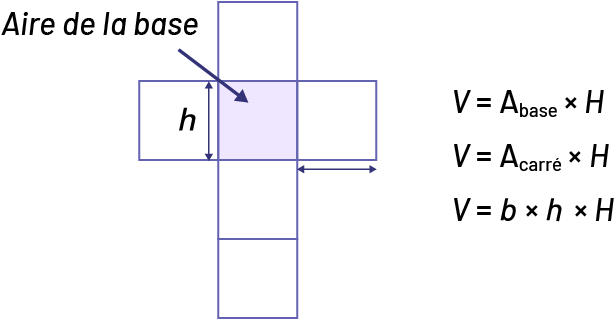
Prisme droit à base triangulaire
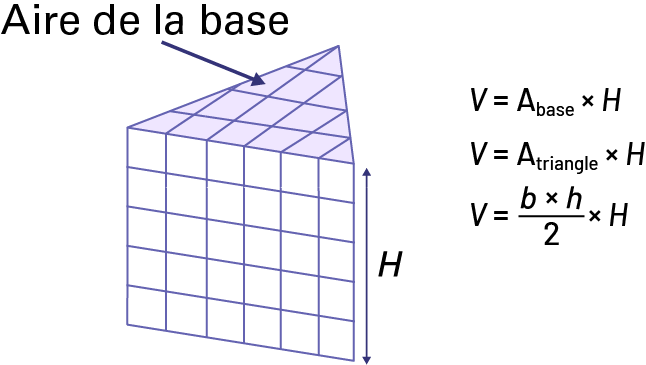
Prisme droit dont la base est un parallélogramme ou prisme oblique à base rectangulaire
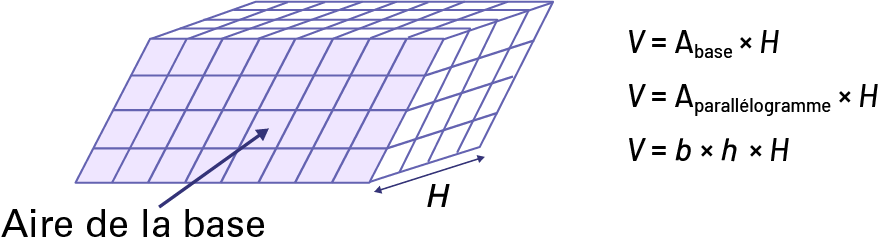
Volume d’un cylindre. Mesure de l’espace qu’occupe un cylindre.
Note : Comme pour les prismes, chaque étage (tranche) d’un cylindre est identique.
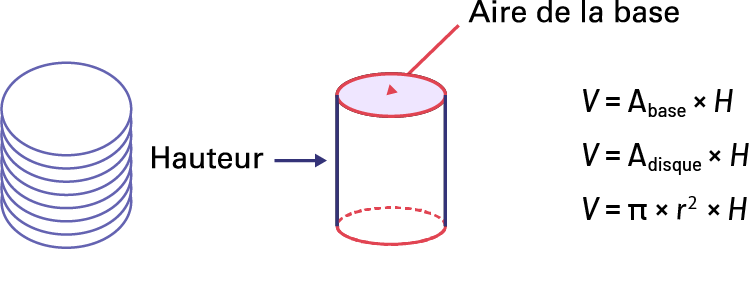
Source : En avant, les maths!, 7e année, CM, Sens de l’espace, p. 2-3.
CONNAISSANCE : CAPACITÉ
Capacité. Quantité de liquide, de grains ou de tout autre objet qui comble l’espace utilisable d’un récipient. La capacité d’un contenant désigne donc la quantité maximale d’une substance donnée qu’il est possible de mettre à l’intérieur du contenant.
Pour trouver la mesure de la capacité d’un contenant, on se sert de la mesure de son volume intérieur. La mesure de la capacité s’exprime en litres (par exemple, l, ml, cl, dl).
Il existe des relations entre les unités métriques de capacité et de volume : 1 ml de liquide occupe 1 cm3 d’espace et un récipient de 1 l a un volume intérieur de 1 000 cm3.
Source : Curriculum de l’Ontario. Programme-cadre de mathématiques de la 1re à la 8e année. 2020. Ministère de l’Éducation de l’Ontario.
Dans le cas d’un contenant, il importe de faire la différence entre son volume extérieur et son volume intérieur (capacité).
Exemples
Le coffre ci-dessous a un volume extérieur de 1 500 cm3 et un volume intérieur de 832 cm3.
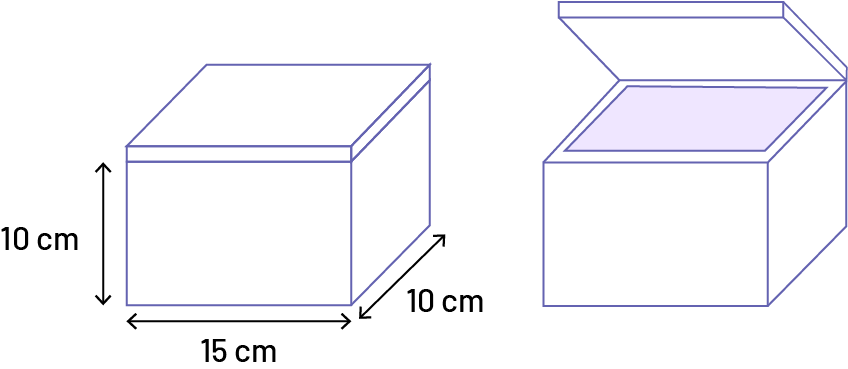
Le volume du liquide dans la bouteille est égal à 275 ml.

Source : Fiche de la 4e à la 6e année_Attribut volume, p. 2.
CONNAISSANCE : VOLUME
Volume d’un prisme. Mesure en unités cubes de l’espace à trois dimensions occupé par un objet solide. On mesure habituellement le volume en centimètres cubes et en mètres cubes.
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
Le volume désigne la grandeur d’un espace à trois dimensions qu’occupe un objet (y compris toute matière solide, liquide ou gazeuse), tandis que la capacité d’un contenant désigne la quantité maximale d’une substance donnée qu’il est possible de mettre à l’intérieur du contenant.
Exemple
Je compare le volume de deux contenants en vérifiant celui qui occupe le plus d’espace (par exemple, par déplacement d’eau).
Je détermine la capacité d’un thermos en y transvidant des tasses d’eau.
Source : adaptation de Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 41-42.
Concepts fondamentaux
Conservation
L’élève qui comprend ce concept réalise que, dans la plupart des situations, le volume d’un objet demeure le même que l’objet soit déplacé, transformé ou décomposé.
Exemple
Une bouteille contient 250 ml de jus de fruits. Lise transvide ce jus dans un verre dont la capacité est supérieure à la capacité de la bouteille. Quel sera le volume du jus dans le verre? (Le volume du jus dans le verre demeure le même, soit 250 ml, car le déplacement du jus d’un contenant à un autre n’en change pas le volume.)
Additivité
L’élève qui comprend ce concept réalise que le volume d’un objet est égal à la somme du volume de chacune de ses parties.
Exemple
Un prisme à base rectangulaire ayant un volume de 1 500 cm3 est composé d’un certain nombre de pièces de format différent. Karla a trouvé un sac contenant quatre pièces qui ont respectivement un volume de 234 cm3, 416 cm3, 98 cm3 et 585 cm3. A-t-elle trouvé toutes les pièces du prisme? (Non, car le volume total des pièces trouvées est égal à 1 333 cm3, alors que le prisme complet a un volume de 1 500 cm3.)
Structure associée aux unités de mesure d’un prisme droit à base rectangulaire
L’élève qui comprend ce concept réalise que les unités de mesure de volume sont d’abord placées, sans espace ni chevauchement, de façon à former des dispositions rectangulaires d’unités cubiques et que ces dispositions rectangulaires sont ensuite juxtaposées en une troisième dimension pour créer un prisme droit à base rectangulaire.
Exemple
Conrad veut déterminer le volume du prisme illustré ci-dessous en considérant la juxtaposition de dispositions rectangulaires formées de cubes. Il pourrait le faire de trois façons différentes. Lesquelles?

Il pourrait considérer qu’il y a :
- trois dispositions rectangulaires qui sont composées de cinq colonnes et de quatre rangées. Le volume du prisme est donc égal à 3 × [5 × 4] = 60 cubes.
- quatre dispositions rectangulaires qui sont composées de cinq colonnes et de trois rangées. Le volume du prisme est donc égal à 4 × [5 × 3] = 60 cubes.
- cinq dispositions rectangulaires qui sont composées de trois colonnes et de quatre rangées. Le volume du prisme est donc égal à 5 × [3 × 4] = 60 cubes.
Source : Fiche de la 4e à la 6e année_Attribut volume, p. 2.
