La vue d'ensemble

À vue d'oeil...

un remaniement des guides d'enseignement efficace en mathématiques

FrançaisEnglish

E2.6 Représenter des cylindres sous forme de développements et déterminer leur aire totale en faisant la somme des aires de leurs faces.

HABILETÉ : REPRÉSENTER DES CYLINDRES SOUS FORME DE DÉVELOPPEMENTS

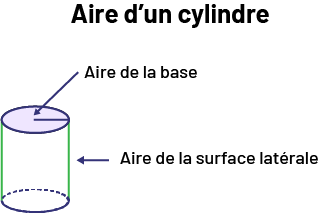
Lorsqu’on représente un cylindre sous forme de développements, la surface latérale est en fait un rectangle replié sur lui-même pour former un cercle et dont la base est la circonférence de ce cercle.

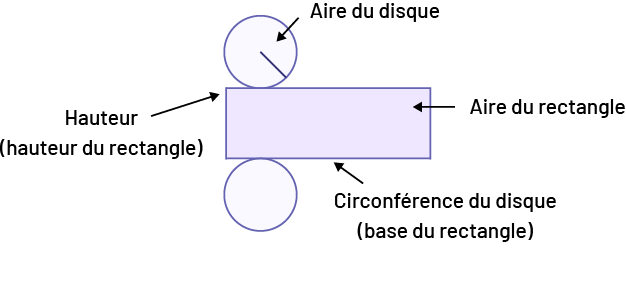
Aire d’un cylindre. La base circulaire d’un cylindre représente l’aire de la base. La surface cylindrique du côté représenter est l’aire de la surface latérale.Développement d’un cylindre. Les cercles représentent l’aire du disque. LE rectangle représente l’aire du re4ctangle. Lec ôté largeur du rectangle est la hauteur. Et la longueur du rectangle représente la circonférence du disque.

Source : adapté de En avant, les maths!, 7e année, CM, Sens de l’espace, p. 5.

HABILETÉ : DÉTERMINER L’AIRE TOTALE DE CYLINDRES EN FAISANT LA SOMME DES AIRES DE LEURS FACES

L’aire est additive : cela signifie que des aires partielles peuvent être additionnées pour trouver une aire complète. Ainsi, le calcul de l’aire totale d’un cylindre se traduit par l’application de la propriété d’additivité.

Les développements permettent de visualiser les figures planes qui composent un objet tridimensionnel, comme un cylindre. Les bases des cylindres consistent en deux faces parallèles congruentes (voir le contenu d’apprentissage E1.1 pour une liste complète des propriétés des cylindres) reliées par un rectangle (ce qui produit un cylindre droit) ou reliées par un parallélogramme non rectangulaire (ce qui produit un cylindre oblique).

Dans la vie de tous les jours, des cylindres peuvent sembler avoir deux bases (par exemple, boîtes de conserve fermées), une base (par exemple, porte-crayons cylindriques) ou aucune base (par exemple, tuyaux, rouleaux d’essuie-tout).

Remarque : Pour visualiser le développement d’un cylindre, il faut reconnaître les figures qui représentent ses faces et comprendre la façon dont les dimensions du cylindre se rapportent aux dimensions des différentes faces.

Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.

Aire d’un cylindre. La base circulaire d’un cylindre représente l’aire de la base. La surface cylindrique du côté représenter est l’aire de la surface latérale.

\(\begin{align} A_{totale} &= {\color{green}A_{surface \ latérale}} + 2 \times {\color{purple}A_{base}} \\ &= {\color{green}b \times h} + 2 \times {\color{purple}\pi r^{2}} \\ &= {\color{green}C \times H} + 2 \times {\color{purple}\pi r^{2}} \\ &= {\color{green}\pi d \times H} + 2 \times {\color{purple}\pi r^{2}} \\ &ou \\ &= {\color{green}2 \pi r^{2} \times H} + 2 \times {\color{purple}\pi r^{2}} \end{align}\)

Source : En avant, les maths!, 7e année, CM, Sens de l’espace, p. 5.